Zadanie ZM-1523
o zadaniu...
- Publikacja w Delcie: marzec 2017
- Publikacja elektroniczna: 1 marca 2017
Wielokąt wypukły został podzielony odcinkami na skończoną liczbę czworokątów. Udowodnić, że co najmniej jeden z nich jest wypukły.
Wielokąt wypukły został podzielony odcinkami na skończoną liczbę czworokątów. Udowodnić, że co najmniej jeden z nich jest wypukły.
Pięciokąt 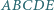 jest wpisany w okrąg
jest wpisany w okrąg 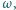 przy czym proste
przy czym proste 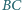 i
i 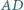 przecinają się w takim punkcie
przecinają się w takim punkcie 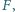 że prosta
że prosta 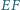 jest styczna do
jest styczna do 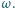 Druga prosta styczna do okręgu
Druga prosta styczna do okręgu 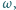 równoległa do
równoległa do 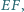 przecina proste
przecina proste 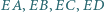 odpowiednio w punktach
odpowiednio w punktach 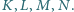 Udowodnić, że odcinki
Udowodnić, że odcinki 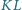 i
i 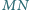 mają jednakową długość.
mają jednakową długość.
Wierzchołek czworościanu nazwijmy ciekawym, jeśli z trzech wychodzących zeń krawędzi nie da się zbudować trójkąta.
W pewnym wierzchołku mapy spotykają się dokładnie trzy państwa. Czy oznacza to, że mapy tej nie da się pomalować dwoma kolorami?
Bazgroł to narysowana ołówkiem na kartce ciągła krzywa zamknięta, przy czym nie wolno rysować drugi razy wzdłuż narysowanej już linii (również w przypadku więcej niż jednego bazgroła na kartce). Jeśli dwa bazgroły mają wspólny punkt, to się w nim przecinają. Wykaż, że:
W każdym wierzchołku danego wielościanu wypukłego schodzi się parzysta liczba krawędzi. Wykaż, że dowolny przekrój tego wielościanu płaszczyzną nieprzechodzącą przez żaden wierzchołek jest wielokątem o parzystej liczbie boków.
W trójkącie 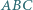 bok
bok 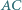 jest dłuższy niż
jest dłuższy niż 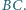 Punkt
Punkt 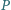 leży na dwusiecznej
leży na dwusiecznej 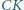 kąta
kąta 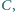 zaś punkt
zaś punkt 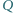 leży na środkowej
leży na środkowej 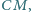 połowiącej bok
połowiącej bok 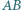 ; przy tym
; przy tym 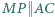 oraz
oraz 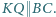 Wykazać, że odcinek
Wykazać, że odcinek 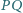 jest prostopadły do
jest prostopadły do 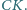
Dany jest sześciokąt wypukły 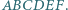 Każda z przekątnych
Każda z przekątnych 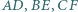 dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
dzieli ten sześciokąt na dwa czworokąty o równych polach. Udowodnij, że przekątne te przecinają się w jednym punkcie.
Twierdzenie (Pascala). Punkty 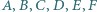 leżą na jednym okręgu. Proste
leżą na jednym okręgu. Proste 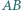 i
i 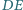 przecinają się w punkcie
przecinają się w punkcie 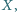 proste
proste 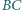 i
i 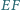 w punkcie
w punkcie 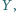 proste
proste 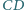 i
i 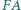 w punkcie
w punkcie 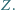 Wykaż, że wówczas punkty
Wykaż, że wówczas punkty 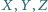 leżą na jednej prostej.
leżą na jednej prostej.
Okręgi 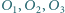 są styczne odpowiednio do par boków
są styczne odpowiednio do par boków 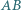 i
i 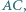
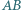 i
i 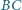 oraz
oraz 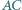 i
i 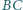 trójkąta
trójkąta 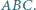 Okrąg
Okrąg 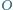 jest styczny zewnętrznie do okręgów
jest styczny zewnętrznie do okręgów 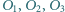 odpowiednio w punktach
odpowiednio w punktach 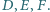 Wykaż, że proste
Wykaż, że proste 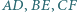 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Dany jest równoległobok 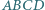 oraz punkt
oraz punkt 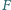 leżący na odcinku
leżący na odcinku 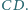 Punkty
Punkty 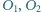 i
i 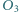 są środkami okręgów opisanych na trójkątach
są środkami okręgów opisanych na trójkątach 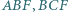 i
i 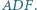 Dowieść, że ortocentrum trójkąta
Dowieść, że ortocentrum trójkąta 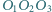 leży na prostej
leży na prostej 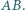
W czworokącie 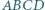 opisanym na okręgu prosta
opisanym na okręgu prosta 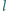 przechodząca przez wierzchołek
przechodząca przez wierzchołek 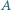 przecina bok
przecina bok 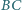 w punkcie
w punkcie 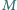 oraz półprostą
oraz półprostą 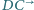 w punkcie
w punkcie 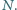 Punkty
Punkty 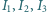 są środkami okręgów wpisanych odpowiednio w trójkąty
są środkami okręgów wpisanych odpowiednio w trójkąty 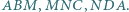 Dowieść, że punkt przecięcia wysokości trójkąta
Dowieść, że punkt przecięcia wysokości trójkąta 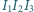 leży na prostej
leży na prostej 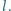
Dane są punkty 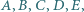 takie, że czworokąt
takie, że czworokąt 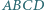 jest równoległobokiem, a czworokąt
jest równoległobokiem, a czworokąt 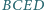 jest wpisany w okrąg. Prosta
jest wpisany w okrąg. Prosta 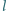 przechodząca przez
przechodząca przez 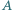 przecina wnętrze odcinka
przecina wnętrze odcinka 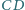 w punkcie
w punkcie 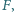 a prostą
a prostą 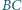 w punkcie
w punkcie 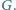 Przypuśćmy, że
Przypuśćmy, że 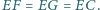 Wykazać, że
Wykazać, że 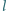 jest dwusieczną kąta
jest dwusieczną kąta 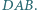
Dany jest trójkąt 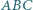 wpisany w okrąg
wpisany w okrąg 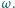 Punkt
Punkt 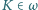 i punkt
i punkt 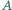 leżą po przeciwnych stronach prostej
leżą po przeciwnych stronach prostej 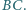 Punkty
Punkty 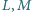 są odbiciami punktu
są odbiciami punktu 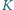 względem
względem 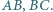 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 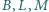 przecina
przecina 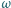 po raz drugi w punkcie
po raz drugi w punkcie 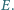 Punkt
Punkt 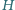 jest ortocentrum trójkąta
jest ortocentrum trójkąta 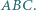 Wykazać, że proste
Wykazać, że proste 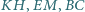 mają punkt wspólny.
mają punkt wspólny.
W trójkącie 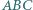 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków 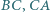 i
i 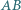 w punktach odpowiednio
w punktach odpowiednio 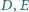 i
i 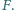 Punkt
Punkt 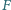 jest punktem Feuerbacha trójkąta
jest punktem Feuerbacha trójkąta 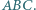 Wówczas prosta Simsona punktu
Wówczas prosta Simsona punktu 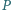 względem trójkąta
względem trójkąta 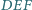 jest równoległa do prostej
jest równoległa do prostej 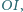 która łączy środki
która łączy środki 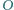 i
i 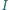 - okręgów opisanego i wpisanego trójkąta
- okręgów opisanego i wpisanego trójkąta 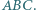
Czworokąt wypukły 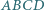 o obwodzie
o obwodzie 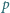 został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie
został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie 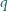 . Wykazać, że pole
. Wykazać, że pole 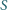 czworokąta
czworokąta 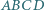 jest mniejsze niż
jest mniejsze niż 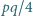 .
.
Trójkąt równoboczny o boku długości 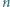 został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 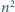 trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
Wyznaczyć wszystkie liczby naturalne 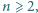 dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.
dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.
Czy z prostopadłościennych klocków o wymiarach 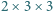 można ułożyć prostopadłościan o wymiarach
można ułożyć prostopadłościan o wymiarach 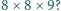
Z kostek domina o wymiarach 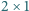 ułożono szachownicę
ułożono szachownicę 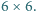 Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Z klocków o wymiarach 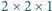 zbudowano sześcian
zbudowano sześcian 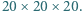 Wykaż, że istnieje taka prosta równoległa do jednej z krawędzi sześcianu i przechodząca przez jego wnętrze, która nie przecina wnętrza żadnego z klocków.
Wykaż, że istnieje taka prosta równoległa do jednej z krawędzi sześcianu i przechodząca przez jego wnętrze, która nie przecina wnętrza żadnego z klocków.
Udowodnij, że po usunięciu z kwadratu o krawędzi 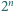 dowolnego spośród
dowolnego spośród 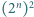 tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami
tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami 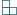 , zbudowanymi z trzech kwadratów jednostkowych.
, zbudowanymi z trzech kwadratów jednostkowych.
Klockiem nazwiemy bryłę otrzymaną przez usunięcie z sześcianu o krawędzi 2 jednego spośród ośmiu sześcianów jednostkowych, z których jest on zbudowany. Udowodnij, że po usunięciu z sześcianu o krawędzi 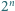 dowolnego spośród
dowolnego spośród 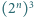 tworzących go sześcianów jednostkowych powstaje bryła, którą daje się szczelnie wypełnić klockami.
tworzących go sześcianów jednostkowych powstaje bryła, którą daje się szczelnie wypełnić klockami.
W czworokącie wypukłym 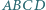 kąty przy wierzchołkach
kąty przy wierzchołkach 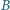 i
i 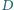 są proste. Przekątne przecinają się w punkcie
są proste. Przekątne przecinają się w punkcie 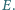 Prosta prostopadła do
Prosta prostopadła do 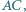 przechodząca przez punkt
przechodząca przez punkt 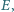 przecina proste
przecina proste 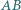 i
i 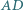 w punktach
w punktach 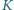 i
i 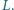 Wykazać, że punkty
Wykazać, że punkty 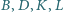 leżą na jednym okręgu.
leżą na jednym okręgu.