Zadania z matematyki - III 2020»
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - III 2020
- Publikacja w Delcie: marzec 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Punkt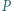 
leży wewnątrz trójkąta ostrokątnego 
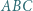i nie jest środkiem okręgu 
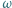opisanego na tym trójkącie. Udowodnić, że wśród odcinków 
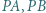i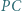 
znajdują się odcinek krótszy oraz odcinek dłuższy od promienia okręgu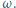 
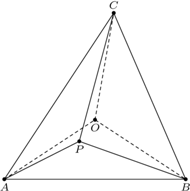
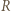leży wewnątrz trójkąta 
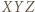i 
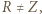to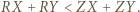 
Aby go udowodnić, zauważmy najpierw, że 
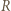nie leży na co najmniej jednym z odcinków 
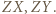Bez straty ogólności przyjmijmy, że jest to 
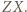Niech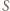 
będzie punktem przecięcia prostych 
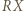i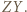 
Wtedy z nierówności trójkąta: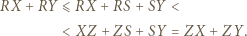
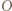będzie środkiem okręgu 
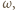a 
będzie promieniem tego okręgu. Punkt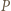 
leży w co najmniej jednym z trójkątów 
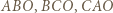; bez straty ogólności przyjmijmy, że jest to trójkąt 
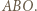Podobnie, 
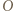leży w którymś z trójkątów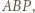 
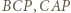; przyjmijmy, że jest to trójkąt 
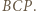Zgodnie z lematem zachodzi 
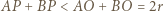; i analogicznie: 
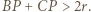Zatem któryś z odcinków 
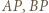jest mniejszy od 
i któryś z odcinków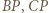 
jest większy od 