Klub 44M - zadania IX 2019»Zadanie 785
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania IX 2019
- Publikacja w Delcie: wrzesień 2019
- Publikacja elektroniczna: 1 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (310 KB)
Pięciokąt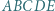 
jest wpisany w okrąg o środku 
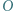; przy tym 
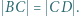Przekątne 
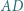i 
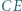są prostopadłe, zaś przekątne 
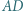i 
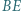przecinają się w takim punkcie 
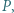że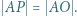 
Wykazać, że trójkąt 
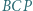jest równoboczny.
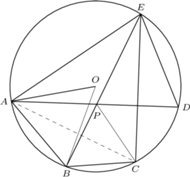
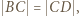punkt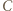 
jest środkiem łuku 
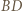; zatem prosta 
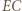jest dwusieczną kąta wpisanego 
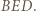Przy tym jest prostopadła do prostej 
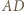; jest więc symetralną odcinka 
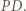Stąd wynika, że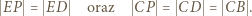
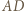i 
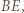przecinające się w punkcie 
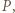wyznaczają trójkąty podobne: 
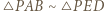; a ponieważ 
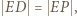zatem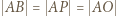 
(ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt 
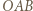jest równoboczny, wobec czego 
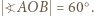W takim razie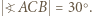 
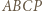to deltoid 
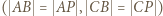; stąd 
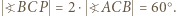Wobec wcześniejszego spostrzeżenia, że 
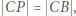dostajemy tezę zadania: trójkąt 
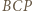jest równoboczny.