Zadanie

Udowodnić, że jeśli punkty 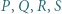$|P,Q,$ tworzą układ ortocentryczny, to:

(a): punkt symetryczny do 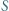$S$ względem prostej 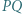$P Q$ leży na okręgu opisanym na trójkącie $PQR$ ;
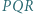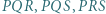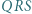(b): okręgi opisane na trójkątach $P | QR,$ i $|QRS$ mają równe promienie;
(c): punkt symetryczny do 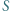$S$ względem środka odcinka 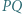$|PQ$ leży na okręgu opisanym na trójkącie $|PQR$ ;
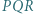(d): $PQ$ ;
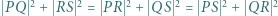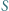(e): punkt $|S$ jest środkiem okręgu wpisanego lub dopisanego do trójkąta utworzonego przez spodki układu.

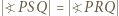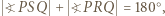(a): Przeprowadzając odpowiedni rachunek na kątach, wykazać, że $?P SQ$ lub $?P SQ$ w zależności od umiejscowienia punktu 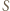$|S$ względem pozostałych.
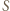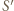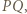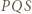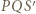(b): Jeśli punkty $S$ i $|S′$ są symetryczne względem prostej $PQ,$ to okręgi opisane na trójkątach $PQS$ i $P | QS$ również. Wystarczy skorzystać z poprzedniego podpunktu.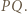
(c): Okręgi wspomniane w poprzednim podpunkcie są również środkowosymetryczne względem środka odcinka $P| Q.$
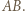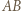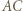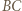(d): Najpierw wyznaczamy środek odcinka $AB.$ Okrąg o średnicy $AB$ przecina proste $AC |$ i $BC |$ w punktach, które są spodkami wysokości trójkąta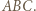 $ABC. |$
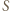(e): Rozważyć dwa przypadki - punkt $S |$ wewnątrz i na zewnątrz trójkąta 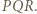$PQR.$ Do rachunków na kątach wykorzystać okręgi, o których była mowa we wstępie.