Zadanie ZM-1607
o zadaniu...
- Publikacja w Delcie: lipiec 2019
- Publikacja elektroniczna: 1 lipca 2019
Dana jest triangulacja pewnego 
-kąta o tej własności, że w każdym wierzchołku tego trójkąta schodzi się nieparzysta liczba trójkątów tej triangulacji. Wykazać, że 
jest liczbą podzielną przez 3.
Co to jest triangulacja
Triangulacją 
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na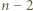 
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
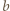i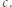 
-kąta należą do trójkątów triangulacji tego samego koloru; bez straty ogólności przypuśćmy, że jest to kolor czarny. Tymczasem każda przekątna triangulacji jest bokiem dokładnie jednego trójkąta czarnego i jednego trójkąta białego. Stąd wniosek, że łączna liczba narysowanych przekątnych jest równa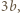 
a łączna liczba boków 
-kąta i narysowanych przekątnych jest równa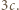 
W konsekwencji 