Kąty płaskie w przestrzeni»Zadanie 10
o zadaniu...
- Zadanie pochodzi z artykułu Kąty płaskie w przestrzeni
- Publikacja w Delcie: czerwiec 2011
- Publikacja elektroniczna: 31-05-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (53 KB)
Dane są dwa wypukłe kąty bryłowe o wspólnym wierzchołku, z których jeden leży wewnątrz drugiego. Dowieść, że suma miar kątów płaskich kąta leżącego wewnątrz jest mniejsza niż suma miar kątów płaskich kąta leżącego na zewnątrz.
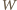 jest wspólnym wierzchołkiem danych dwóch
kątów oraz przyjmijmy, że pewna płaszczyzna przecinająca wszystkie
ściany obywdu kątów tworzy w przekroju wewnętrznego kąta wielokąt
jest wspólnym wierzchołkiem danych dwóch
kątów oraz przyjmijmy, że pewna płaszczyzna przecinająca wszystkie
ściany obywdu kątów tworzy w przekroju wewnętrznego kąta wielokąt
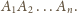 Niech ponadto półprosta
Niech ponadto półprosta
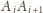 przecina zewnętrzny
kąt w punkcie
przecina zewnętrzny
kąt w punkcie
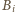 (jak zwykle idneksowanie modulo
(jak zwykle idneksowanie modulo
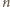 ). Dla
). Dla
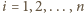 zachodzą nierówności
zachodzą nierówności
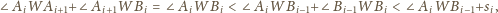
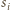 jest sumą kątów płaskich przy wierzchołku
jest sumą kątów płaskich przy wierzchołku
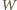 części
kąta zewnętrznego ograniczonej płaszczyznami
części
kąta zewnętrznego ograniczonej płaszczyznami
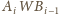 i
i
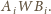 Dodając te wszystkie nierówności stronami dostajemy
tezę.
Dodając te wszystkie nierówności stronami dostajemy
tezę.
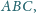 w którym
w którym
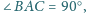 jest podstawą ostrosłupa
jest podstawą ostrosłupa
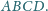 Ponadto zachodzą równości
Ponadto zachodzą równości

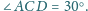
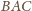 uzupełniamy do prostokąta
uzupełniamy do prostokąta
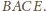 Wówczas z
równości
Wówczas z
równości
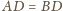 wynika, że
wynika, że
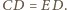 To w połączeniu z
To w połączeniu z
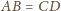 dowodzi, że trójkąt
dowodzi, że trójkąt
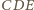 jest równoboczny.
Zatem
jest równoboczny.
Zatem
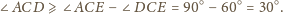
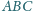 o kącie prostym
przy wierzchołku
o kącie prostym
przy wierzchołku
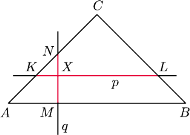
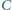 . Znaleźć zbiór takich punktów
. Znaleźć zbiór takich punktów
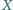 z wnętrza trójkąta
z wnętrza trójkąta
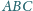 , że jeśli prosta
, że jeśli prosta
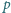 równoległa do
podstawy
równoległa do
podstawy
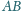 przechodząca przez punkt
przechodząca przez punkt
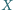 przecina ramiona
przecina ramiona
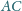 i
i
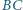 w punktach
w punktach
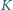 i
i
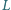 , zaś
, zaś
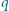 jest prostą
prostopadłą do
jest prostą
prostopadłą do
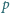 przechodzącą przez
przechodzącą przez
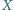 , przecinającą podstawę
, przecinającą podstawę
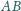 trójkąta w punkcie
trójkąta w punkcie
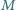 , a ramię w punkcie
, a ramię w punkcie
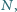 to
to
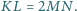
 przecina ramię
przecina ramię
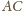 . Rozszerzmy nasz
trójkąt do kwadratu
. Rozszerzmy nasz
trójkąt do kwadratu
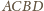 .
.
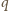 z nowo dorysowanym bokiem kwadratu
oznaczmy przez
z nowo dorysowanym bokiem kwadratu
oznaczmy przez
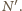 Szukamy takich punktów
Szukamy takich punktów
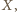 że
że
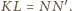 Równoważnie takich, że odcinki
Równoważnie takich, że odcinki
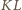 i
i
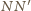 są symetryczne względem prostej
są symetryczne względem prostej
 prostopadłej do
prostopadłej do
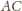 przechodzącej przez
przechodzącej przez
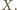 To zachodzi wtedy i tylko wtedy, gdy
trójkąty
To zachodzi wtedy i tylko wtedy, gdy
trójkąty
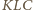 i
i
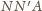 są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
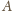 i
i
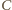 są symetryczne
względem
są symetryczne
względem
 (bo punkty
(bo punkty
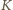 i
i
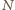 zostały skonstruowane tak,
że są symetryczne względem
zostały skonstruowane tak,
że są symetryczne względem
 ).
).
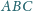 punkt
punkt
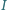 jest środkiem okręgu
wpisanego, stycznego do boków
jest środkiem okręgu
wpisanego, stycznego do boków
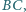
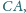
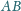 odpowiednio
w punktach
odpowiednio
w punktach
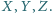 Proste
Proste
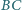 i
i
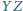 przecinają się
w punkcie
przecinają się
w punkcie
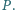 Dowieść, że proste
Dowieść, że proste
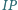 i
i
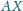 są
prostopadłe.
są
prostopadłe.
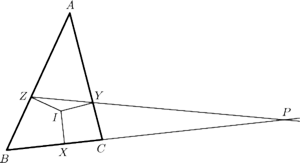
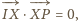
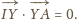 Punkt
Punkt
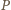 leży na prostej
leży na prostej
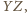 prostopadłej do
prostopadłej do
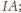 zatem
zatem
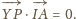
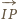 i
i
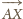 są prostopadłe.
Obliczamy ich iloczyn skalarny:
są prostopadłe.
Obliczamy ich iloczyn skalarny:
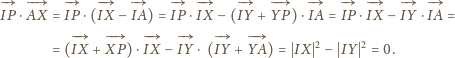
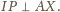
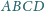 i
i
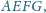 tak samo zorientowane, mają wspólny
tylko punkt
tak samo zorientowane, mają wspólny
tylko punkt
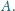 Wykaż, że
Wykaż, że
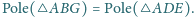
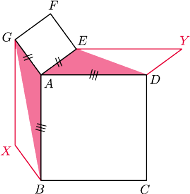
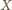 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
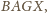 a
a
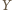 – czwartym wierzchołkiem równoległoboku
– czwartym wierzchołkiem równoległoboku
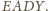 Równoległoboki te są przystające, ponieważ
Równoległoboki te są przystające, ponieważ
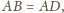
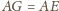 oraz
oraz
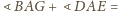
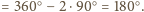 Stąd
Stąd
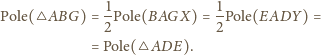
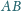 i
i
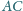 trójkąta
trójkąta
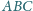 zbudowano, po jego
zewnętrznej stronie, kwadraty
zbudowano, po jego
zewnętrznej stronie, kwadraty
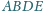 i
i
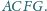 Punkty
Punkty
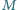 i
i
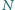 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
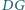 i
i
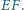 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia
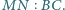
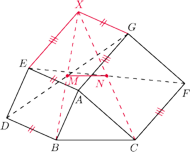
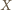 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
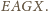 Wtedy
Wtedy
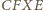 także jest równoległobokiem (bo
także jest równoległobokiem (bo
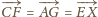 ). Wobec tego punkt
). Wobec tego punkt
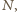 jako środek jego przekątnej
jako środek jego przekątnej
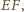 jest też środkiem drugiej przekątnej
jest też środkiem drugiej przekątnej
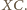 Analogicznie
Analogicznie
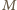 jest środkiem
jest środkiem
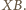 Stąd i z twierdzenia Talesa uzyskujemy
Stąd i z twierdzenia Talesa uzyskujemy
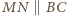 oraz
oraz
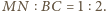
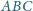 zachodzi równość
zachodzi równość
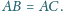 Punkt
Punkt
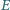 jest środkiem wysokości
jest środkiem wysokości
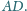 Punkt
Punkt
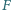 jest rzutem
prostokątnym punktu
jest rzutem
prostokątnym punktu
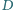 na prostą
na prostą
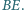 Udowodnij, że
Udowodnij, że
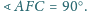
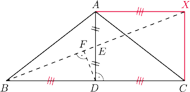
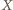 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
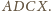 Wtedy
Wtedy
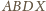 jest równoległobokiem o środku
jest równoległobokiem o środku
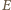 (bo
(bo
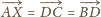 oraz
oraz
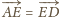 ), więc punkty
), więc punkty
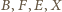 są
współliniowe. Odcinki
są
współliniowe. Odcinki
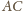 i
i
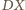 są średnicami okręgu opisanego
na prostokącie
są średnicami okręgu opisanego
na prostokącie
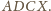 Ponadto
Ponadto
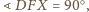 więc punkt
więc punkt
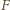 leży na tym okręgu. Stąd
leży na tym okręgu. Stąd
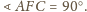
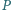 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
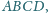 przy czym
przy czym
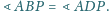 Wykaż, że
Wykaż, że
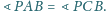
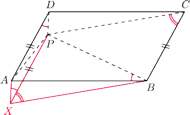
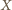 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
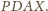 Wtedy
Wtedy
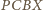 także jest równoległobokiem oraz
zachodzą równości
także jest równoległobokiem oraz
zachodzą równości
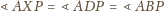
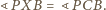
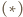 (uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
(uwzględniając wzajemne położenie odpowiednich
punktów) wynika, że punkty
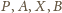 leżą na jednym okręgu. Wobec
tego
leżą na jednym okręgu. Wobec
tego
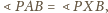 co razem z równością
co razem z równością
 daje tezę.
daje tezę.
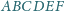 o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
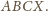 Wtedy
Wtedy
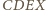 i
i
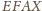 też są równoległobokami...
też są równoległobokami...
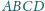 punkty
punkty
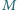 i
i
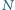 są środkami odpowiednio
ramion
są środkami odpowiednio
ramion
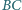 i
i
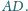 Wykaż, że
Wykaż, że
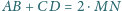 i że
i że


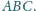 Wykaż, że z jego środkowych można
zbudować trójkąt.
Wykaż, że z jego środkowych można
zbudować trójkąt.
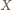 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
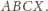
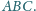 Punkty
Punkty
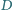 i
i
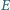 należą odpowiednio do boków
należą odpowiednio do boków
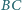 i
i
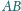 tego
trójkąta i
tego
trójkąta i
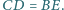 Punkt
Punkt
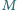 jest środkiem odcinka
jest środkiem odcinka
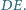 Udowodnij, że
Udowodnij, że
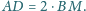
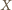 będzie czwartym wierzchołkiem równoległoboku
będzie czwartym wierzchołkiem równoległoboku
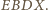
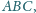 w którym
w którym
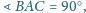 jest podstawą
ostrosłupa
jest podstawą
ostrosłupa
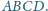 Ponadto zachodzą równości
Ponadto zachodzą równości
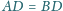 oraz
oraz
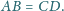 Wykaż, że
Wykaż, że
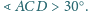
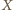 będzie czwartym wierzchołkiem prostokąta
będzie czwartym wierzchołkiem prostokąta
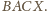
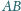 i
i
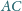 trójkąta
trójkąta
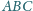 zbudowano po
zewnętrznej stronie podobne trójkąty prostokątne
zbudowano po
zewnętrznej stronie podobne trójkąty prostokątne
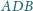 i
i
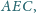 w
których kąty przy wierzchołkach
w
których kąty przy wierzchołkach
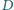 i
i
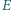 są proste. Punkt
są proste. Punkt
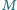 jest środkiem odcinka
jest środkiem odcinka
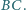 Udowodnić, że
Udowodnić, że
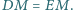
 i
i
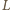 oznaczają punkty symetryczne do
oznaczają punkty symetryczne do
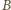 i
i
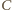 względem punktów
względem punktów
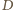 i
i
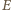 odpowiednio.
odpowiednio.
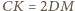 i
i
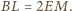 Zauważmy, że trójkąty
Zauważmy, że trójkąty
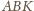 i
i
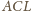 są równoramienne:
są równoramienne:
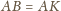 i
i
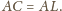 Ponadto, ponieważ
Ponadto, ponieważ
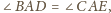 więc
więc
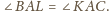 Wobec tego trójkąty
Wobec tego trójkąty
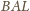 i
i
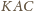 są
przystające. To oznacza, że
są
przystające. To oznacza, że
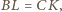 co wraz z pierwszą obserwacją
kończy dowód.
co wraz z pierwszą obserwacją
kończy dowód.
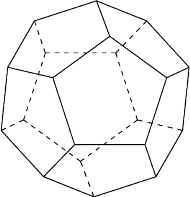
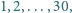 używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była: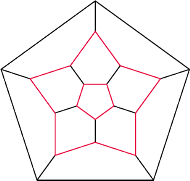
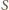 oznacza sumę wszystkich numerów
krawędzi:
oznacza sumę wszystkich numerów
krawędzi:
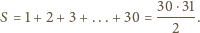
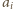 oznacza sumę numerów w
oznacza sumę numerów w
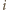 -tym wierzchołku (
-tym wierzchołku (
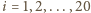 ). Wtedy
). Wtedy
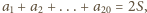 bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
bo numer każdej
krawędzi jest liczony dwukrotnie – przy każdym z jej końców. Gdyby
każda z liczb
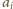 była podzielna przez 4, to
była podzielna przez 4, to
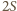 także. Jednak
także. Jednak
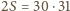 nie dzieli się przez 4.
nie dzieli się przez 4.
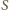 oznacza ich sumę, a
oznacza ich sumę, a
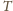 – sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
– sumę pozostałych czterech liczb.
Opisana operacja nie zmienia
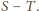 Początkowo
Początkowo
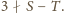 Tymczasem gdyby
Tymczasem gdyby
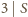 i
i
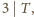 to
to
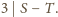
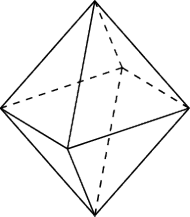
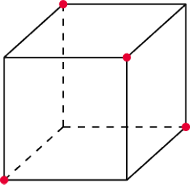
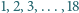 można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.
można rozstawić w wierzchołkach
i na środkach krawędzi ośmiościanu foremnego, tak aby każda
liczba na krawędzi ośmiościanu była średnią arytmetyczną liczb na jej
końcach.
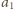 i
i
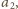
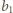 i
i
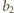 oraz
oraz
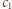 i
i
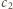 liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
liczby zapisane na parach przeciwległych ścian sześcianu.
Zauważmy, że w każdym wierzchołku występuje inny spośród ośmiu
możliwych iloczynów
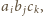 gdzie
gdzie
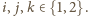 Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako
Suma liczb
w wierzchołkach jest więc sumą tych ośmiu iloczynów i można ją zapisać
jako
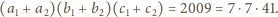
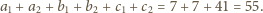
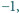 a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
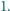 Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
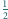 w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
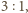 licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
licząc od wierzchołka. Punkt ten jest jednocześnie środkiem kuli wpisanej i
opisanej na czworościanie foremnym.
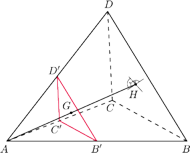
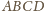 można wpisać kulę
można wpisać kulę
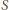 o środku
o środku
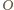 i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
i promieniu 1, wysokość tego czworościanu wynosi 4
(na podstawie przytoczonej własności). Przekształćmy czworościan
foremny
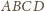 przez jednokładność względem punktu
przez jednokładność względem punktu
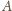 o skali
o skali
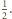 W efekcie otrzymamy czworościan
W efekcie otrzymamy czworościan
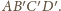 Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
Korzystając z własności jednokładności, wnioskujemy, że płaszczyzna
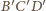 przecina wysokość
przecina wysokość
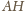 w punkcie
w punkcie
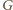 w taki
sposób, że
w taki
sposób, że
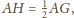 a kula
a kula
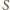 jest również styczna do
płaszczyzny
jest również styczna do
płaszczyzny
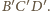 Zatem kula
Zatem kula
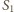 wpisana w czworościan
wpisana w czworościan
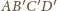 ma promień
ma promień
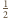 i ma tylko jeden punkt wspólny z kulą
i ma tylko jeden punkt wspólny z kulą
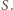
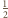 umieszczone w każdym „rogu” czworościanu
umieszczone w każdym „rogu” czworościanu
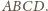 Każda z tych kul
ma tylko jeden punkt wspólny z kulą
Każda z tych kul
ma tylko jeden punkt wspólny z kulą
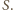 Ponieważ kula
Ponieważ kula
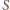 ma
promień 1, więc można umieścić w niej dwie kule o promieniu
ma
promień 1, więc można umieścić w niej dwie kule o promieniu
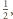 które mają tylko jeden punkt wspólny.
które mają tylko jeden punkt wspólny.
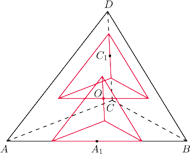
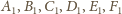 będą odpowiednio środkami krawędzi
będą odpowiednio środkami krawędzi
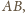
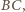
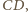
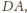
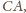
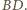 Przekształćmy kulę
Przekształćmy kulę
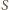 i czworościan
i czworościan
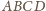 przez
przez 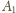 i skali
i skali
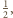
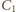 i skali
i skali
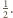
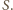 Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
Zatem kule wpisane w te
czworościany nie mają punktów wspólnych.
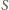 przez
przez 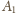 i skali
i skali
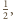
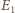 i skali
i skali
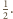
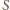 będą środki kul o promieniach
będą środki kul o promieniach
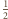 znajdujące się w połowie odcinków
znajdujące się w połowie odcinków
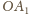 i
i
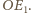 Wykażemy teraz,
że kule te nie mają punktów wspólnych.
Wykażemy teraz,
że kule te nie mają punktów wspólnych.
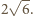 Zatem odległość
punktów
Zatem odległość
punktów
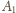 i
i
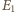 wynosi
wynosi
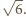 Środki boków
Środki boków
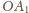 i
i
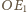 w trójkącie
w trójkącie
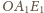 pozostają w odległości
pozostają w odległości
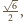 która
jest większa od 1.
która
jest większa od 1.
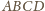 można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
można umieścić sześć
kul: każda z nich jest obrazem kuli wpisanej w czworościan
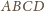 w
jednokładności o skali
w
jednokładności o skali
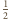 i środku będącym środkiem krawędzi
czworościanu.
i środku będącym środkiem krawędzi
czworościanu.
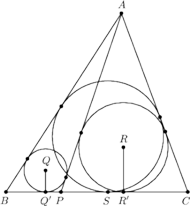
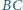 trójkąta
trójkąta
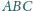 wybrano punkt
wybrano punkt
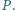 Punkty
Punkty
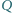 i
i
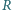 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty
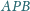 i
i
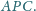 Punkt
Punkt
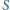 jest punktem styczności okręgu wpisanego w trójkąt
jest punktem styczności okręgu wpisanego w trójkąt
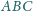 do boku
do boku
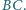 Wykazać, że punkty
Wykazać, że punkty
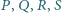 leżą na
jednym okręgu.
leżą na
jednym okręgu.
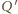 i
i
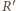 oznaczają rzuty punktów
oznaczają rzuty punktów
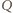 i
i
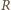 na
prostą
na
prostą
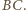 Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
Z przyrównania odcinków stycznych do okręgu wpisanego
w trójkącie
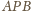 wynika równość
wynika równość
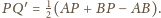 Podobnie mamy
Podobnie mamy
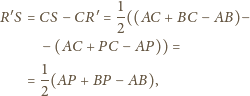
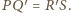 Stąd również
Stąd również
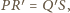 czyli
czyli
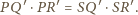
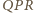 między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
między dwusiecznymi kątów przyległych jest prosty,
więc trójkąty prostokątne
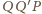 i
i
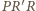 są podobne. W takim
razie
są podobne. W takim
razie
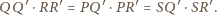
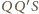 i
i
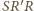 są podobne, więc kąt
są podobne, więc kąt
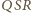 też
jest prosty. To oznacza, że punkty
też
jest prosty. To oznacza, że punkty
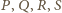 leżą na jednym
okręgu.
leżą na jednym
okręgu.
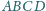 jest styczna do ścian
jest styczna do ścian
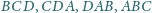 odpowiednio w punktach
odpowiednio w punktach
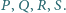 Odcinek
Odcinek
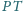 jest średnicą tej sfery, zaś punkty
jest średnicą tej sfery, zaś punkty
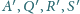 są
punktami przecięcia prostych
są
punktami przecięcia prostych
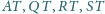 z płaszczyzną
z płaszczyzną
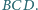 Dowieść , że punkt
Dowieść , że punkt
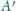 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
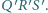
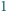 od jego wierzchołków jest
nie większa niż
od jego wierzchołków jest
nie większa niż
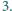
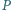 leżącego
wewnątrz trójkąta równobocznego
leżącego
wewnątrz trójkąta równobocznego
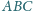 o boku
o boku
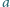 od jego
wierzchołków jest nie większa niż
od jego
wierzchołków jest nie większa niż
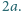
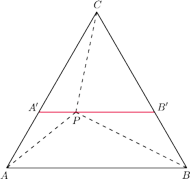
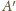 i
i
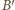 będą punktami przecięcia prostej równoległej
do
będą punktami przecięcia prostej równoległej
do
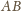 i przechodzącej przez punkt
i przechodzącej przez punkt
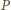 odpowiednio z bokami
odpowiednio z bokami
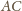 i
i
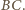 Trójkąt
Trójkąt
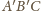 jest równoboczny i
jest równoboczny i
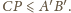 Ponadto stosując nierówność trójkąta, dostaniemy
Ponadto stosując nierówność trójkąta, dostaniemy
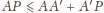 oraz
oraz
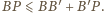 Dodając te trzy nierówności stronami,
otrzymujemy
Dodając te trzy nierówności stronami,
otrzymujemy
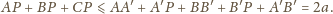
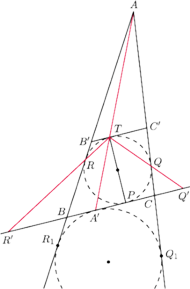
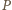 jest jednym z wierzchołków trójkąta
jest jednym z wierzchołków trójkąta
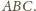
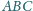 jest styczny do boków
jest styczny do boków
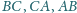 odpowiednio w punktach
odpowiednio w punktach
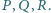 Odcinek
Odcinek
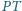 jest średnicą tego
okręgu. Proste
jest średnicą tego
okręgu. Proste
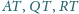 przecinają prostą
przecinają prostą
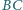 odpowiednio
w punktach
odpowiednio
w punktach
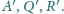 Wykazać, że
Wykazać, że
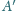 jest środkiem odcinka
jest środkiem odcinka
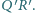
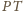 jest średnicą, to styczna do okręgu wpisanego w punkcie
jest średnicą, to styczna do okręgu wpisanego w punkcie
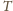 jest równoległa do
jest równoległa do
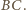 Niech
Niech
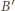 i
i
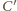 będą punktami
przecięcia tej stycznej z bokami
będą punktami
przecięcia tej stycznej z bokami
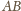 i
i
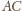 (
(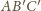 i
i
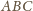 są jednokładne, skąd natychmiast wynika, że
punkt
są jednokładne, skąd natychmiast wynika, że
punkt
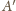 jest punktem styczności okręgu dopisanego z bokiem
jest punktem styczności okręgu dopisanego z bokiem
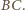 Z równoległości
Z równoległości
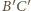 i
i
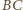 wynika też, że trójkąty
wynika też, że trójkąty
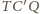 i
i
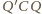 są podobne, a skoro
są podobne, a skoro
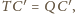 to
to
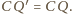 Niech
Niech
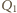 będzie punktem styczności okręgu
dopisanego, stycznego do
będzie punktem styczności okręgu
dopisanego, stycznego do
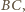 z prostą
z prostą
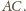 W takim razie
W takim razie
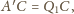 a stąd natychmiast wynika, że
a stąd natychmiast wynika, że
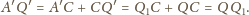
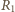 punkt styczności okręgu dopisanego
z bokiem
punkt styczności okręgu dopisanego
z bokiem
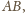 udowodnimy, że
udowodnimy, że
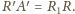 Ale
Ale
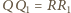 – dowód jest więc zakończony.
– dowód jest więc zakończony.
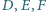 należą odpowiednio do boków
należą odpowiednio do boków
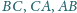 trójkąta
trójkąta
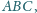 proste
proste
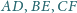 przecinają się w punkcie
przecinają się w punkcie
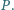 Wykaż, że
Wykaż, że

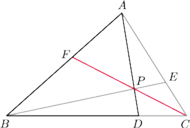
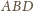 i prostej
i prostej
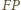 zachodzi
zachodzi
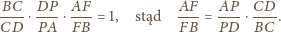
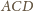 i prostej
i prostej
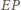 otrzymujemy
otrzymujemy

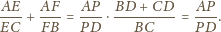
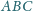 punkty
punkty
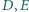 są spodkami dwusiecznych
odpowiednio
są spodkami dwusiecznych
odpowiednio
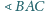 i
i
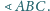 Punkt
Punkt
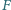 jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
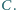 Udowodnij, że
punkty
Udowodnij, że
punkty
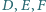 leżą na jednej prostej.
leżą na jednej prostej.
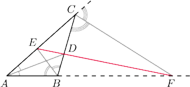
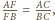
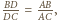
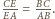 Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
Zachodzi więc równość z Twierdzenie Menelaosa, co
kończy dowód.
 jest styczna do krawędzi
jest styczna do krawędzi
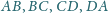 czworościanu
czworościanu
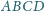 dpowiednio w punktach
dpowiednio w punktach
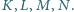 Wykaż, że leżą one
na jednej płaszczyźnie.
Wykaż, że leżą one
na jednej płaszczyźnie.
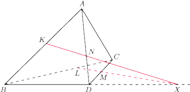
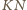 przecina prostą
przecina prostą
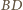 w pewnym punkcie
w pewnym punkcie
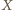 (poza odcinkiem
(poza odcinkiem
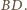 Wtedy z twierdzenia Menelaosa dla
trójkąta
Wtedy z twierdzenia Menelaosa dla
trójkąta
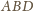 i prostej
i prostej
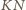 mamy
mamy
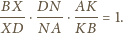
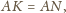
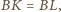
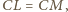
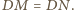 Wobec powyższego
Wobec powyższego
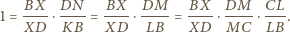
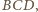 prosta
prosta
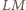 przecina prostą
przecina prostą
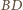 w punkcie
w punkcie
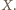 Stąd proste
Stąd proste
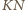 i
i
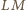 przecinają się, więc punkty
przecinają się, więc punkty
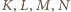 leżą na jednej
płaszczyźnie. Prostszy przypadek
leżą na jednej
płaszczyźnie. Prostszy przypadek
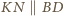 pozostawiam jako
ćwiczenie.
pozostawiam jako
ćwiczenie.
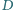 i
i
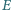 leżą odpowiednio na bokach
leżą odpowiednio na bokach
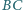 i
i
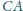 trójkąta
trójkąta
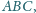 a punkt
a punkt
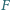 na przedłużeniu boku
na przedłużeniu boku
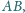 przy czym punkty
przy czym punkty
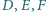 są współliniowe. Punkty
są współliniowe. Punkty
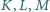 są odpowiednio środkami boków
są odpowiednio środkami boków
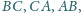 zaś punkty
zaś punkty
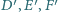 – obrazami symetrycznymi punktów
– obrazami symetrycznymi punktów
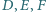 w symetriach względem
w symetriach względem
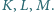 Wykaż, że punkty
Wykaż, że punkty
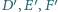 są
współliniowe.
są
współliniowe.