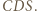Potęga punktu względem okręgu»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Potęga punktu względem okręgu
- Publikacja w Delcie: listopad 2019
- Publikacja elektroniczna: 31 października 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (417 KB)
Dany jest trapez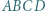 
o podstawach 
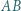i 
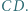Okręgi o średnicach 
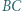i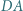 
przecinają się w punktach 
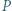i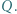 
Przekątne trapezu przecinają się w punkcie 
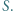Dowieść, że punkty 
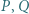i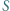 
leżą na jednej prostej.
Wskazówka
Prosta 
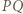jest osią potęgową pary okręgów z zadania, więc wystarczy wykazać, że punkt 
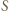ma jednakową względem nich potęgę. Można to zrobić za pomocą podobieństwa trójkątów 
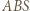i 