Klub 44M - zadania VI 2019»Zadanie 783
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania VI 2019
- Publikacja w Delcie: czerwiec 2019
- Publikacja elektroniczna: 31 maja 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (256 KB)
Na płaszczyźnie narysowano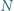 
kwadratów o bokach równoległych i prostopadłych do ustalonego wspólnego kierunku. Niech 
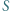będzie zbiorem środków tych kwadratów; zakładamy, że jest to 
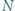różnych punktów oraz że żaden punkt zbioru 
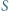nie leży na brzegu żadnego kwadratu. Udowodnić, że można wyróżnić niektóre z tych 
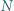kwadratów tak, by każdy punkt zbioru 
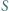leżał w co najmniej jednym wyróżnionym kwadracie oraz w co najwyżej czterech wyróżnionych kwadratach.
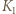będzie największym spośród 
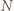kwadratów (jeśli jest kilka przystających, większych od pozostałych, wybieramy dowolny). Niech 
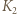będzie największym spośród tych, których środki nie leżą w 
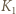; itd. (indukcja): niech 
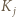będzie największym spośród tych, których środki nie leżą w 
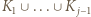; gdy takich kwadratów już nie ma, kończymy numerowanie. Ponumerowane kwadraty 
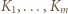będą tymi "wyróżnionymi". Zbiór 
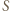zawiera się w 
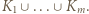Przy tym środek żadnego wyróżnionego kwadratu nie leży w żadnym innym wyróżnionym kwadracie.
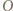któregokolwiek spośród pozostałych kwadratów leży w co najmniej pięciu wyróżnionych kwadratach. Przyjmujemy punkt 
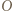za początek układu współrzędnych 
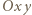o osiach równoległych do boków kwadratów (jednostkę długości wybieramy dowolnie). Osie dzielą płaszczyznę na cztery ćwiartki, więc pewne dwa wyróżnione kwadraty 
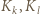(zawierające 
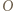) mają środki 
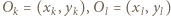położone w jednej ćwiartce. Bez straty ogólności przyjmijmy, że 
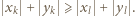Wówczas 
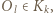wbrew wcześniejszemu spostrzeżeniu. Sprzeczność kończy dowód.