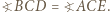Składanie inwersji z symetrią»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Składanie inwersji z symetrią
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (390 KB)
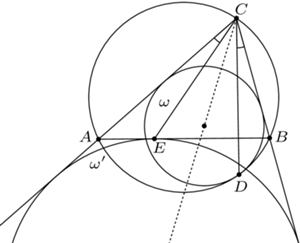
Dany jest trójkąt 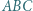 wpisany w okrąg
wpisany w okrąg  Okrąg
Okrąg 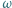 jest styczny do odcinków
jest styczny do odcinków 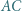 i
i 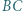 oraz do okręgu
oraz do okręgu  w punkcie
w punkcie 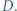 Okrąg
Okrąg 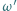 zaś jest dopisany do trójkąta
zaś jest dopisany do trójkąta 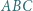 i styczny do boku
i styczny do boku 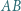 w punkcie
w punkcie 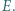 Wykazać, że
Wykazać, że 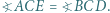

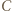 i promieniu
i promieniu 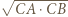 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 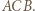 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 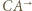 i
i 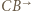 oraz prostą
oraz prostą 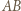 z okręgiem
z okręgiem 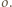 W takim razie okrąg
W takim razie okrąg 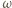 przejdzie na okrąg styczny do prostej
przejdzie na okrąg styczny do prostej 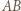 i półprostych
i półprostych 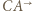 i
i 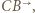 czyli na okrąg
czyli na okrąg 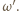 Stąd wniosek, że obrazem punktu
Stąd wniosek, że obrazem punktu 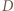 jest punkt
jest punkt 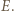 Półprosta
Półprosta 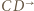 przejdzie więc na półprostą
przejdzie więc na półprostą 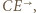 a skoro inwersja zachowuje kąty, to
a skoro inwersja zachowuje kąty, to