Klub 44M - zadania III 2020»Zadanie 797
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania III 2020
- Publikacja w Delcie: marzec 2020
- Publikacja elektroniczna: 1 marca 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (342 KB)
W trójkącie 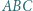 wysokość poprowadzona z wierzchołka
wysokość poprowadzona z wierzchołka 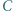 ma długość
ma długość 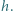 Punkty
Punkty 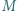 i
i 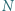 to (odpowiednio) środki boków
to (odpowiednio) środki boków 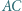 i
i 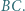 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 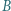 i
i 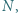 styczny do prostej
styczny do prostej 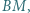 przecina prostą
przecina prostą 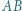 ponownie w punkcie
ponownie w punkcie 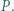 Wyznaczyć największą liczbę
Wyznaczyć największą liczbę 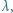 dla której (przy każdej takiej konfiguracji) odcinek
dla której (przy każdej takiej konfiguracji) odcinek 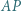 ma długość nie mniejszą niż
ma długość nie mniejszą niż 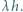


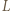 będzie środkiem boku
będzie środkiem boku 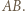 W okręgu
W okręgu 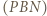 kąt wpisany oparty na cięciwie
kąt wpisany oparty na cięciwie 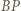 przystaje do kąta między tą cięciwą a styczną w punkcie
przystaje do kąta między tą cięciwą a styczną w punkcie 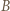 :
: 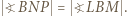 W połączeniu z oczywistą równością
W połączeniu z oczywistą równością 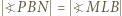 daje to podobieństwo trójkątów
daje to podobieństwo trójkątów 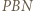 i
i 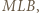 więc i proporcję
więc i proporcję 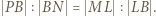 Przy oznaczeniach
Przy oznaczeniach 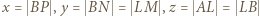 uzyskana proporcja pokazuje, że
uzyskana proporcja pokazuje, że 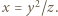 Oznaczając dalej
Oznaczając dalej 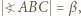 dostajemy ciąg zależności
dostajemy ciąg zależności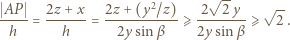
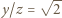 oraz
oraz 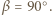 Nierówność
Nierówność 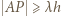 zachodzi więc dla wartości
zachodzi więc dla wartości 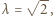 której powiększyć już nie można.
której powiększyć już nie można.