Ekstrema»Zadanie 7
Na płaszczyźnie dany jest skończony zbiór punktów, z których żadne trzy nie leżą na jednej prostej. Wykaż, że można wśród nich znaleźć trzy takie, iż poprowadzony przez nie okrąg nie zawiera we wnętrzu innych punktów tego zbioru.
Na płaszczyźnie dany jest skończony zbiór punktów, z których żadne trzy nie leżą na jednej prostej. Wykaż, że można wśród nich znaleźć trzy takie, iż poprowadzony przez nie okrąg nie zawiera we wnętrzu innych punktów tego zbioru.
Każdy punkt płaszczyzny pomalowano na biało, czarno lub zielono. Udowodnić, że istnieją dwa punkty w odległości 1, które są tego samego koloru.
Znaleźć wszystkie trójkąty ostrokątne
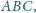 wpisane w ustalony
okrąg
wpisane w ustalony
okrąg
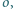 spełniające następujący warunek: środek ciężkości
spełniające następujący warunek: środek ciężkości
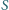 trójkąta
trójkąta
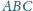 pokrywa się z ortocentrum
pokrywa się z ortocentrum
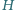 trójkąta
trójkąta
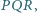 gdzie
gdzie
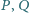 i
i
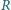 to odpowiednio punkty przecięcia
półprostych
to odpowiednio punkty przecięcia
półprostych
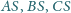 z okręgiem
z okręgiem
Multimilioner leci z Oslo (ok.
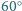 N,
N,
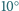 E) do cioci, mieszkającej
w Ameryce Południowej, w pewnym dużym mieście prawie na równiku.
Gdzie mieszka ciocia, jeśli prywatny odrzutowiec multimilionera, lecący do niej
najkrótszą drogą, startuje w tym celu dokładnie w kierunku zachodnim? Jaka
jest odległość pomiędzy Oslo a miastem cioci (obwód Ziemi to około
E) do cioci, mieszkającej
w Ameryce Południowej, w pewnym dużym mieście prawie na równiku.
Gdzie mieszka ciocia, jeśli prywatny odrzutowiec multimilionera, lecący do niej
najkrótszą drogą, startuje w tym celu dokładnie w kierunku zachodnim? Jaka
jest odległość pomiędzy Oslo a miastem cioci (obwód Ziemi to około
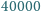 km)?
km)?
Ile trzeba zrobić zdjęć globusa, by w sumie uwiecznić na nich każde miejsce na Ziemi? Podpórkę od globusa, zasłaniającą być może fragmenty, zaniedbujemy.
Czy na powierzchni Ziemi istnieje taki trójkąt o bokach wyznaczonych przez najkrótsze drogi pomiędzy wierzchołkami, który ma wszystkie kąty proste?
Wędrowiec poszedł 10 km na południe, potem 10 km cały czas na wschód, wzdłuż równoleżnika, następnie 10 km na północ i wrócił w ten sposób do punktu wyjścia. Spotkał tam pewne zwierzę. Jeśli był to niedźwiedź, to jakiego koloru? Czy mógł to być pingwin?
Pola wszystkich przekrojów równoległościanu
 płaszczyznami
przechodzącymi przez środki trzech jego krawędzi, z których żadne dwie nie
są równoległe i nie mają punktów wspólnych, są równe. Udowodnić, że
równoległościan
płaszczyznami
przechodzącymi przez środki trzech jego krawędzi, z których żadne dwie nie
są równoległe i nie mają punktów wspólnych, są równe. Udowodnić, że
równoległościan
 jest prostopadłościanem.
jest prostopadłościanem.
Czy w przestrzeni trójwymiarowej można znaleźć takie punkty
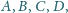 dla których spełnione są warunki:
dla których spełnione są warunki:

Dany jest czworościan
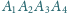 . Przez
. Przez
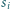 oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
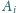 i kuli wpisanej w ten czworościan. Wiadomo, że
i kuli wpisanej w ten czworościan. Wiadomo, że
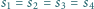 . Rozstrzygnąć, czy czworościan ten musi być
foremny.
. Rozstrzygnąć, czy czworościan ten musi być
foremny.
Sfera wpisana w czworościan jest styczna do dwóch ścian w środkach okręgów opisanych, a do trzeciej w ortocentrum. Dowieść, że czworościan ten jest foremny.
Czy mając dane promienie sfer dopisanych do czworościanu oraz promień sfery wpisanej w ten czworościan można wyznaczyć jego objętość?
Czworokąt
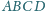 jest wpisany w okrąg. Boki
jest wpisany w okrąg. Boki
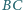 i
i
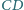 mają
jednakową długość. Na przedłużeniu odcinka
mają
jednakową długość. Na przedłużeniu odcinka
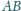 odkładamy odcinek
odkładamy odcinek
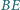 długości
długości
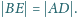 Dowieść, że
Dowieść, że
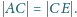
Każdy punkt płaszczyzny pomalowano na biało lub czarno. Rozstrzygnąć, czy istnieje niezdegenerowany do punktu odcinek jednokolorowy.
Udowodnij, że wśród dowolnych
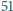 wierzchołków
wierzchołków
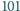 -kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.
-kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.
W trójkącie ostrokątnym
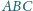 punkt
punkt
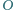 jest środkiem okręgu
opisanego, a dwusieczna kąta
jest środkiem okręgu
opisanego, a dwusieczna kąta
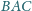 przecina bok
przecina bok
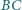 w punkcie
w punkcie
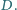 Niech
Niech
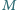 będzie takim punktem, że
będzie takim punktem, że
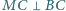 oraz
oraz
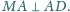 Proste
Proste
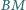 i
i
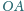 przecinają się w punkcie
przecinają się w punkcie
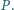 Wykazać, że okrąg o środku
Wykazać, że okrąg o środku
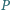 i przechodzący przez punkt
i przechodzący przez punkt
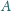 jest styczny do prostej
jest styczny do prostej
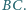

Dany jest nierównoramienny trójkąt prostokątny
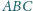 o kącie
prostym przy wierzchołku
o kącie
prostym przy wierzchołku
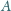 . Niech
. Niech
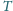 będzie środkiem
okręgu wpisanego, zaś
będzie środkiem
okręgu wpisanego, zaś
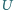 i
i
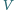 niech będą jego punktami
styczności odpowiednio z bokami
niech będą jego punktami
styczności odpowiednio z bokami
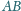 i
i
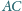 . Prosta
. Prosta
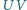 przecina w punkcie
przecina w punkcie
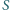 styczną do okręgu opisanego poprowadzoną
w punkcie
styczną do okręgu opisanego poprowadzoną
w punkcie
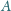 . Udowodnić, że proste
. Udowodnić, że proste
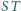 i
i
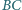 są równoległe.
są równoległe.
Udowodnij, że suma
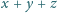 nie zależy od położenia punktu
nie zależy od położenia punktu
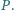
Punkt
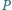 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
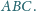 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
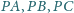 można zbudować
trójkąt.
można zbudować
trójkąt.
Wyznacz miary kątów trójkąta o bokach
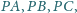 jeśli
jeśli
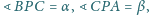
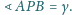
Punkt
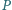 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
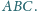 Wyznacz
pole trójkąta
Wyznacz
pole trójkąta
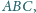 jeśli
jeśli
Punkt
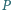 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
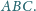 Udowodnij, że
Udowodnij, że
Czy na powierzchni każdego czworościanu można wskazać takie cztery punkty, które są wierzchołkami kwadratu, i z których żadne dwa nie leżą na jednej ścianie tego czworościanu? Odpowiedź uzasadnij.