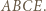Przez linie będziemy rozumieli odcinki łączące przeciwległe boki zadanego kwadratu 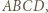 prostopadłe do nich i przebiegające przez punkty kratowe. Gdy długość boku jest liczbą nieparzystą, żądane pokolorowanie da się banalnie wykonać: malujemy każdą linię (w całości) pojedynczym kolorem; linie równoległe do
prostopadłe do nich i przebiegające przez punkty kratowe. Gdy długość boku jest liczbą nieparzystą, żądane pokolorowanie da się banalnie wykonać: malujemy każdą linię (w całości) pojedynczym kolorem; linie równoległe do 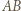 naprzemiennie, dwoma kolorami; linie równoległe do
naprzemiennie, dwoma kolorami; linie równoległe do 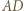 też naprzemiennie, dwoma pozostałymi kolorami.
też naprzemiennie, dwoma pozostałymi kolorami.
Gdy długość boku jest liczbą parzystą - pokolorowanie, o jakim mowa, też jest wykonalne. Niech 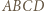 będzie, jak poprzednio, kwadratem o boku długości nieparzystej, z pokolorowaniem opisanym powyżej. Przedłużamy jego boki
będzie, jak poprzednio, kwadratem o boku długości nieparzystej, z pokolorowaniem opisanym powyżej. Przedłużamy jego boki 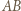 i
i 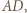 każdy o jednostkę, otrzymując odcinki
każdy o jednostkę, otrzymując odcinki 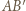 i
i 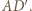 Niech punkt
Niech punkt 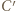 dopełnia kwadrat
dopełnia kwadrat 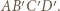 Poprzednie pokolorowanie odcinków
Poprzednie pokolorowanie odcinków 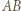 i
i 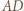 przedłużamy na całe linie
przedłużamy na całe linie 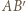 i
i 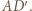 Bok
Bok 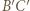 malujemy kolorem odcinka
malujemy kolorem odcinka 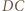 ; bok
; bok 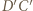 malujemy kolorem odcinka
malujemy kolorem odcinka 
W niewypukłym sześciokącie 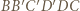 sposób malowania odcinków jednostkowych, równoległych do
sposób malowania odcinków jednostkowych, równoległych do 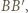 jest już wymuszony przez postawione warunki - zaczynamy od
jest już wymuszony przez postawione warunki - zaczynamy od 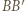 (który już ma kolor) i malujemy kolejne równoległe odcinki, kończąc na tym, który ma jeden koniec w punkcie
(który już ma kolor) i malujemy kolejne równoległe odcinki, kończąc na tym, który ma jeden koniec w punkcie 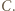 Podobnie postępujemy z odcinkami jednostkowymi, równoległymi do
Podobnie postępujemy z odcinkami jednostkowymi, równoległymi do 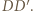 Dzięki założeniu o nieparzystości długości
Dzięki założeniu o nieparzystości długości 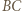 i
i 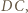 kwadracik o wierzchołkach
kwadracik o wierzchołkach 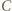 i
i 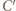 będzie miał brzeg czterobarwny.
będzie miał brzeg czterobarwny.
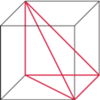
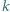 przecinamy płaszczyzną
przecinamy płaszczyzną 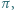 położoną w odległości
położoną w odległości 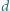 od środka sześcianu. Jaka jest maksymalna wartość
od środka sześcianu. Jaka jest maksymalna wartość 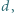 przy której płaszczyzna
przy której płaszczyzna 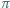 może mieć z każdą ścianą sześcianu co najmniej jeden punkt wspólny?
może mieć z każdą ścianą sześcianu co najmniej jeden punkt wspólny?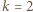 i ustalmy prostokątny układ współrzędnych, w którym wierzchołkami sześcianu są punkty
i ustalmy prostokątny układ współrzędnych, w którym wierzchołkami sześcianu są punkty 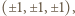 a rzutem prostokątnym punktu
a rzutem prostokątnym punktu 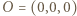 na płaszczyznę
na płaszczyznę 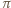 jest punkt
jest punkt 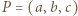 o współrzędnych
o współrzędnych 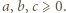 Zatem
Zatem 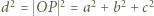 ; zaś płaszczyzna
; zaś płaszczyzna 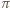 jest dana równaniem
jest dana równaniem 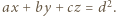
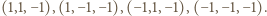 Każda z półprzestrzeni (
Każda z półprzestrzeni ( 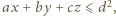
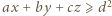 ) musi zawierać jeden z tych czterech wierzchołków. Zatem przy pewnym doborze znaków mamy nierówność
) musi zawierać jeden z tych czterech wierzchołków. Zatem przy pewnym doborze znaków mamy nierówność 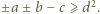 Skoro
Skoro 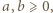 znaczy to, że
znaczy to, że 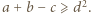
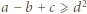 oraz
oraz 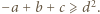 Dodajemy te trzy nierówności i otrzymujemy
Dodajemy te trzy nierówności i otrzymujemy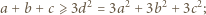
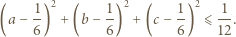
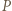 od punktu
od punktu 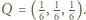 Tak więc
Tak więc 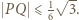 A ponieważ
A ponieważ 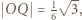 ostatecznie
ostatecznie 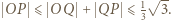
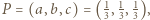 wszystkie nierówności stają się równościami; płaszczyzna o równaniu
wszystkie nierówności stają się równościami; płaszczyzna o równaniu 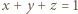 leży w odległości
leży w odległości 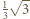 od
od  i spotyka wszystkie ściany. Dla
i spotyka wszystkie ściany. Dla 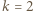 szukane maksimum wynosi więc
szukane maksimum wynosi więc 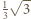 ; zaś w przypadku ogólnym - po przeskalowaniu - wynosi
; zaś w przypadku ogólnym - po przeskalowaniu - wynosi 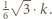
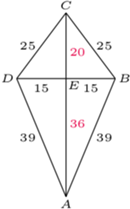
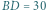
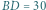
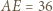 oraz
oraz 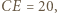 więc
więc 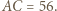
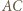 deltoidu może zawierać jego krótszą przekątną (rys. (b)). Wówczas
deltoidu może zawierać jego krótszą przekątną (rys. (b)). Wówczas 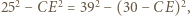 co prowadzi do równości
co prowadzi do równości 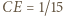 oraz
oraz 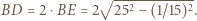
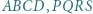 o równych polach i takie, że
o równych polach i takie, że 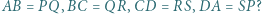

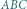
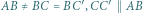
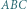
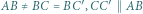
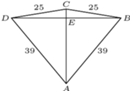
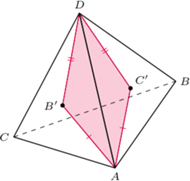
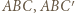 z rysunku mają równe pola i nie są przystające. Niech
z rysunku mają równe pola i nie są przystające. Niech 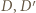 będą obrazami
będą obrazami 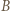 w symetrii odpowiednio względem
w symetrii odpowiednio względem 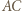 i
i 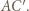 Wówczas deltoidy
Wówczas deltoidy 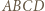 i
i 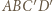 spełniają warunki zadania: mają równe pola i odpowiednie boki oraz nietrudno sprawdzić, że są nieprzystające i wypukłe.
spełniają warunki zadania: mają równe pola i odpowiednie boki oraz nietrudno sprawdzić, że są nieprzystające i wypukłe.
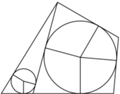
 będą punktami styczności sfery wpisanej w czworościan ze ścianami odpowiednio
będą punktami styczności sfery wpisanej w czworościan ze ścianami odpowiednio 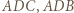 Wówczas
Wówczas 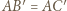 i
i 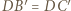 jako odcinki stycznych do tej sfery, więc
jako odcinki stycznych do tej sfery, więc 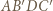 po rozpłaszczeniu jest deltoidem. Podobnie uzyskujemy pozostałe deltoidy.
po rozpłaszczeniu jest deltoidem. Podobnie uzyskujemy pozostałe deltoidy.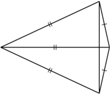
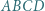 o osi symetrii
o osi symetrii 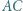 i kątach prostych przy
i kątach prostych przy 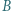 i
i 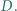 Bila wybita z wierzchołka
Bila wybita z wierzchołka 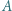 po odbiciu od boku
po odbiciu od boku 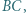 a następnie od
a następnie od 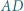 trafia w wierzchołek
trafia w wierzchołek 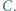 Wykaż, że środek drogi bili leży na
Wykaż, że środek drogi bili leży na 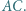
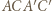 o środku w punkcie
o środku w punkcie 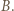 Oznaczmy przez
Oznaczmy przez 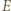 punkt przecięcia drogi bili z odcinkiem
punkt przecięcia drogi bili z odcinkiem 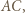 niech
niech 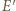 będzie obrazem
będzie obrazem 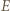 w symetrii względem
w symetrii względem 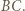 Wystarczy dowieść, że
Wystarczy dowieść, że 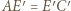 i że odcinki te są równe rozprostowanym odpowiednim fragmentom drogi bili. Przyda się fakt, iż kąt padania bili równy jest kątowi odbicia.
i że odcinki te są równe rozprostowanym odpowiednim fragmentom drogi bili. Przyda się fakt, iż kąt padania bili równy jest kątowi odbicia.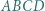 o osi symetrii
o osi symetrii 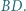 Punkty
Punkty 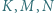 są odpowiednio punktami styczności okręgu wpisanego z bokami
są odpowiednio punktami styczności okręgu wpisanego z bokami 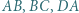 ; proste
; proste 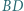 i
i 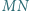 przecinają się w punkcie
przecinają się w punkcie 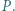 Wykaż, że punkty
Wykaż, że punkty 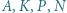 leżą na jednym okręgu.
leżą na jednym okręgu.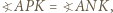 korzystając np. z
korzystając np. z 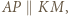 z równoramienności trójkąta
z równoramienności trójkąta 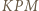 i z twierdzenia o stycznej i cięciwie.
i z twierdzenia o stycznej i cięciwie.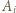 będzie wierzchołkiem kostki, odległym od stołu o
będzie wierzchołkiem kostki, odległym od stołu o 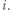 Oznaczmy długość krawędzi kostki przez
Oznaczmy długość krawędzi kostki przez  Łatwo zauważyć, że odcinki
Łatwo zauważyć, że odcinki 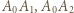 oraz
oraz 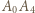 muszą być krawędziami sześcianu (wynika to z faktu, że jeśli krawędziami są
muszą być krawędziami sześcianu (wynika to z faktu, że jeśli krawędziami są 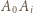 i
i 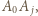 to
to 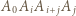 jest ścianą). Niech
jest ścianą). Niech 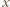 będzie długością krawędzi sześcianu. Dobierzmy układ współrzędnych tak, by
będzie długością krawędzi sześcianu. Dobierzmy układ współrzędnych tak, by 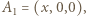
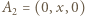 i
i 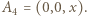 Oznaczmy przez
Oznaczmy przez 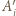 rzut prostokątny punktu
rzut prostokątny punktu 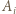 na prostą prostopadłą do stołu, przechodzącą przez
na prostą prostopadłą do stołu, przechodzącą przez 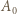 ; wówczas
; wówczas 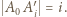 Przyjmijmy
Przyjmijmy 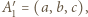 wtedy
wtedy 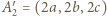 i
i 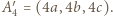 Korzystając z twierdzenia Pitagorasa dla trójkątów prostokątnych
Korzystając z twierdzenia Pitagorasa dla trójkątów prostokątnych 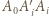 dla
dla 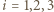 dostajemy
dostajemy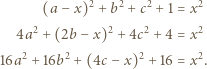
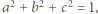 dostajemy
dostajemy 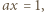
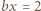 i
i 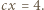 Po podniesieniu ostatnich trzech równości do kwadratu i zsumowaniu, otrzymamy
Po podniesieniu ostatnich trzech równości do kwadratu i zsumowaniu, otrzymamy 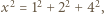 zatem
zatem 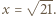

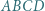 o równoległych podstawach
o równoległych podstawach 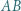 i
i 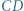 zachodzą równości:
zachodzą równości: 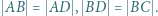 Okrąg opisany na trójkącie
Okrąg opisany na trójkącie 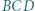 przecina przekątną
przecina przekątną 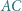 w punkcie
w punkcie 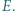 Dowieść, że prosta
Dowieść, że prosta 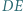 połowi bok
połowi bok 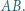

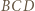 jest równoramienny; symetralna boku
jest równoramienny; symetralna boku 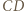 jest osią symetrii tego trójkąta, więc i okręgu na nim opisanego; prosta
jest osią symetrii tego trójkąta, więc i okręgu na nim opisanego; prosta 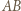 (równoległa do
(równoległa do 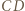 ) jest styczna do tego okręgu. Skoro
) jest styczna do tego okręgu. Skoro 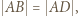 zatem prosta
zatem prosta 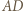 też jest styczna. Wynikają stąd równości kątów
też jest styczna. Wynikają stąd równości kątów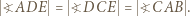
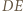 przecina
przecina 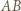 w punkcie, który nazwiemy
w punkcie, który nazwiemy 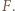 Niech
Niech 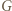 będzie punktem symetrycznym do
będzie punktem symetrycznym do 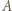 względem
względem 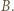 Widzimy trapez równoramienny
Widzimy trapez równoramienny 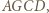 z równymi kątami:
z równymi kątami: 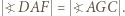 Stąd i z wcześniejszej równości (przepisanej jako
Stąd i z wcześniejszej równości (przepisanej jako 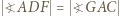 ) wynika podobieństwo trójkątów
) wynika podobieństwo trójkątów 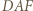 i
i 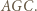 W konsekwencji
W konsekwencji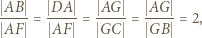
 jest środkiem odcinka
jest środkiem odcinka 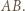
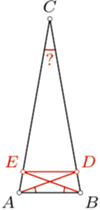
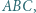 w którym
w którym 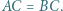 Punkty
Punkty 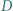 i
i 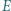 leżą odpowiednio na bokach
leżą odpowiednio na bokach 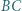 i
i 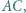 przy czym
przy czym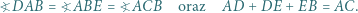
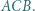
 i
i  będą punktami symetrycznymi do punktów
będą punktami symetrycznymi do punktów 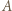 i
i 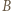 odpowiednio względem prostych
odpowiednio względem prostych 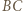 i
i 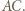 Z danych w treści zadania równości kątów wynika, że punkty
Z danych w treści zadania równości kątów wynika, że punkty 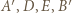 leżą na jednej prostej, a zatem
leżą na jednej prostej, a zatem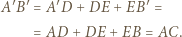
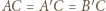 oznacza to, że trójkąt
oznacza to, że trójkąt 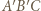 jest równoboczny. W konsekwencji, wobec równości kątów
jest równoboczny. W konsekwencji, wobec równości kątów 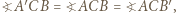 uzyskujemy
uzyskujemy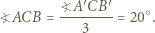
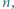 będącej liczbą naturalną, został podzielony prostymi poziomymi i pionowymi na
będącej liczbą naturalną, został podzielony prostymi poziomymi i pionowymi na 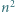 kwadracików jednostkowych. Powstała siatka, utworzona z
kwadracików jednostkowych. Powstała siatka, utworzona z 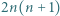 odcinków jednostkowych (boków tych kwadracików). Używając czterech barw, należy te odcinki pokolorować (każdy odcinek jednym kolorem) tak, żeby każdy kwadracik jednostkowy miał boki różnych kolorów oraz by każdy bok dużego kwadratu uzyskał jednolity kolor - ale każdy inny. Dla jakich liczb naturalnych
odcinków jednostkowych (boków tych kwadracików). Używając czterech barw, należy te odcinki pokolorować (każdy odcinek jednym kolorem) tak, żeby każdy kwadracik jednostkowy miał boki różnych kolorów oraz by każdy bok dużego kwadratu uzyskał jednolity kolor - ale każdy inny. Dla jakich liczb naturalnych 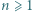 jest to wykonalne?
jest to wykonalne? prostopadłe do nich i przebiegające przez punkty kratowe. Gdy długość boku jest liczbą nieparzystą, żądane pokolorowanie da się banalnie wykonać: malujemy każdą linię (w całości) pojedynczym kolorem; linie równoległe do
prostopadłe do nich i przebiegające przez punkty kratowe. Gdy długość boku jest liczbą nieparzystą, żądane pokolorowanie da się banalnie wykonać: malujemy każdą linię (w całości) pojedynczym kolorem; linie równoległe do  naprzemiennie, dwoma kolorami; linie równoległe do
naprzemiennie, dwoma kolorami; linie równoległe do 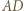 też naprzemiennie, dwoma pozostałymi kolorami.
też naprzemiennie, dwoma pozostałymi kolorami.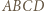 będzie, jak poprzednio, kwadratem o boku długości nieparzystej, z pokolorowaniem opisanym powyżej. Przedłużamy jego boki
będzie, jak poprzednio, kwadratem o boku długości nieparzystej, z pokolorowaniem opisanym powyżej. Przedłużamy jego boki 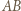 i
i 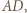 każdy o jednostkę, otrzymując odcinki
każdy o jednostkę, otrzymując odcinki 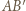 i
i 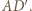 Niech punkt
Niech punkt 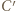 dopełnia kwadrat
dopełnia kwadrat 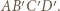 Poprzednie pokolorowanie odcinków
Poprzednie pokolorowanie odcinków 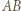 i
i 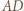 przedłużamy na całe linie
przedłużamy na całe linie 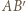 i
i 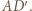 Bok
Bok 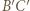 malujemy kolorem odcinka
malujemy kolorem odcinka 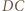 ; bok
; bok 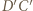 malujemy kolorem odcinka
malujemy kolorem odcinka 
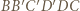 sposób malowania odcinków jednostkowych, równoległych do
sposób malowania odcinków jednostkowych, równoległych do 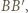 jest już wymuszony przez postawione warunki - zaczynamy od
jest już wymuszony przez postawione warunki - zaczynamy od 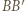 (który już ma kolor) i malujemy kolejne równoległe odcinki, kończąc na tym, który ma jeden koniec w punkcie
(który już ma kolor) i malujemy kolejne równoległe odcinki, kończąc na tym, który ma jeden koniec w punkcie 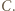 Podobnie postępujemy z odcinkami jednostkowymi, równoległymi do
Podobnie postępujemy z odcinkami jednostkowymi, równoległymi do 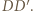 Dzięki założeniu o nieparzystości długości
Dzięki założeniu o nieparzystości długości 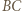 i
i 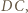 kwadracik o wierzchołkach
kwadracik o wierzchołkach 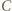 i
i 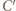 będzie miał brzeg czterobarwny.
będzie miał brzeg czterobarwny.
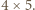 Jeśli jego szerokość 4 powiększyć o
Jeśli jego szerokość 4 powiększyć o 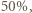 uzyskamy prostokąt o bokach
uzyskamy prostokąt o bokach 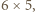 a więc o szerokości 5, czyli o
a więc o szerokości 5, czyli o 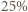 większej niż początkowa. Jeśli zaś długość 5 wyjściowego prostokąta zmniejszyć o
większej niż początkowa. Jeśli zaś długość 5 wyjściowego prostokąta zmniejszyć o 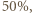 otrzymamy prostokąt rozmiaru
otrzymamy prostokąt rozmiaru 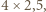 a więc o długości 4, czyli o
a więc o długości 4, czyli o 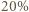 mniejszej niż pierwotna.
mniejszej niż pierwotna.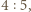 zatem uzyskana powyżej odpowiedź 20% jest jedyną możliwą.
zatem uzyskana powyżej odpowiedź 20% jest jedyną możliwą.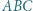 o boku
o boku 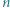 podzielony na
podzielony na 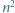 trójkątów równobocznych o boku
trójkątów równobocznych o boku 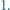 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 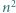 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.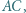 a dwa do
a dwa do 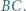
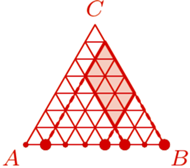
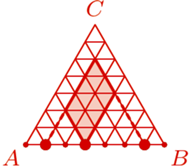
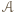 będzie zbiorem
będzie zbiorem 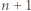 węzłów należących do boku
węzłów należących do boku 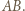
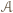 jednoznacznie wyznacza równoległobok o zadanych własnościach, którego punktami przecięcia z
jednoznacznie wyznacza równoległobok o zadanych własnościach, którego punktami przecięcia z 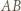 są te cztery punkty i którego "najniższy" wierzchołek nie leży na
są te cztery punkty i którego "najniższy" wierzchołek nie leży na 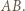 Z kolei każda trójka różnych punktów z
Z kolei każda trójka różnych punktów z 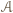 jednoznacznie wyznacza taki równoległobok, którego "najniższy" wierzchołek leży na
jednoznacznie wyznacza taki równoległobok, którego "najniższy" wierzchołek leży na 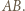
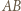 w trzech lub czterech punktach i są to punkty należące do
w trzech lub czterech punktach i są to punkty należące do 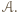 Stąd wniosek, że szukana liczba równoległoboków jest równa łącznej liczbie wyborów trzech lub czterech elementów zbioru
Stąd wniosek, że szukana liczba równoległoboków jest równa łącznej liczbie wyborów trzech lub czterech elementów zbioru 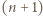 -elementowego, czyli
-elementowego, czyli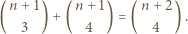
 o boku
o boku  podzielony na
podzielony na  trójkątów równobocznych o boku
trójkątów równobocznych o boku 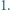 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 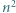 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.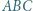 ).
).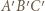 o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli
o wierzchołkach w węzłach nazwijmy czapeczką, jeżeli 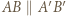 oraz punkty
oraz punkty 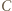 i
i 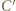 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 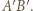
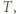 spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli
spełniającemu warunki zadania, przyporządkujmy najmniejszą zawierającą go czapeczkę. Precyzyjniej: jeżeli 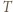 jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do
jest czapeczką, to przyporządkowujemy mu siebie samego, natomiast w przeciwnym przypadku - czapeczkę ograniczoną prostymi: równoległą do 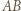 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 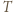 leżący najbliżej
leżący najbliżej 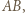 równoległą do
równoległą do 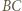 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 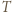 leżący najbliżej
leżący najbliżej 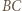 oraz równoległą do
oraz równoległą do 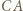 przechodzącą przez wierzchołek
przechodzącą przez wierzchołek 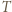 leżący najbliżej
leżący najbliżej 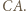
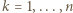 zostało w ten sposób przyporządkowanych dokładnie
zostało w ten sposób przyporządkowanych dokładnie 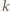 trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku
trójkątów spełniających warunki zadania. Co więcej, liczba czapeczek o boku 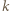 jest równa
jest równa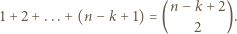
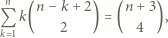
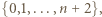 którego drugim co do wielkości elementem jest
którego drugim co do wielkości elementem jest 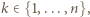 można wybrać na dokładnie
można wybrać na dokładnie 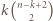 sposobów (wybierając najmniejszy element spośród
sposobów (wybierając najmniejszy element spośród 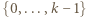 oraz dwa większe od
oraz dwa większe od 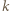 spośród
spośród 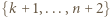 ). Sumując po wszystkich możliwych
). Sumując po wszystkich możliwych 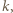 uzyskujemy liczbę sposobów wyboru
uzyskujemy liczbę sposobów wyboru 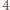 spośród
spośród 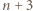 elementów.
elementów.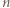 ) oraz w poprzednim (dla trójkąta o boku
) oraz w poprzednim (dla trójkąta o boku 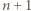 ).
). w którym
w którym 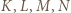 są punktami styczności sfery wpisanej i ścian leżących odpowiednio naprzeciw wierzchołków
są punktami styczności sfery wpisanej i ścian leżących odpowiednio naprzeciw wierzchołków 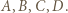
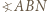 oraz
oraz 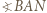 w zależności od miar kątów wewnętrznych ścian czworościanu (które są dane, gdy dana jest siatka).
w zależności od miar kątów wewnętrznych ścian czworościanu (które są dane, gdy dana jest siatka).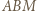 i
i 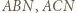 i
i 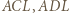 i
i 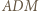 to pary trójkątów przystających; oznaczmy kąty wewnętrzne przy wierzchołku
to pary trójkątów przystających; oznaczmy kąty wewnętrzne przy wierzchołku 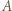 w poszczególnych z nich odpowiednio przez
w poszczególnych z nich odpowiednio przez 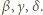 Wówczas
Wówczas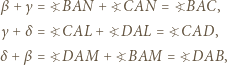
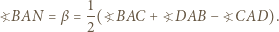
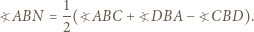
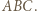 Dla pozostałych ścian konstrukcja jest w pełni analogiczna.
Dla pozostałych ścian konstrukcja jest w pełni analogiczna.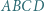 jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek
jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek 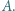 Zakładamy, że proste
Zakładamy, że proste 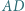 i
i 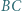 przecinają się w punkcie
przecinają się w punkcie 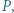 zaś proste
zaś proste 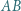 i
i 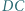 przecinają się w punkcie
przecinają się w punkcie 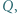 przy czym
przy czym 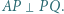 Niech
Niech 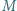 będzie środkiem przekątnej
będzie środkiem przekątnej 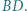 Wykazać, że
Wykazać, że 
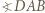 jest najmniejszym kątem czworokąta
jest najmniejszym kątem czworokąta 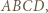 nietrudno wywnioskować, że punkt
nietrudno wywnioskować, że punkt 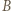 leży między
leży między 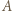 i
i 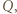 a punkt
a punkt 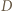 między
między 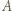 i
i 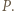 Weźmy pod uwagę okrąg o średnicy
Weźmy pod uwagę okrąg o średnicy 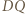 ; ów okrąg przechodzi przez punkt
; ów okrąg przechodzi przez punkt 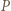 (bo
(bo 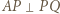 ) oraz przecina odcinek
) oraz przecina odcinek 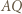 w punkcie, który nazwiemy
w punkcie, który nazwiemy 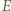 ; zatem
; zatem 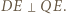
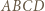 i
i 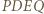 ma okrąg opisany. Wynikają stąd równości kątów
ma okrąg opisany. Wynikają stąd równości kątów 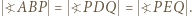 Zatem trójkąt
Zatem trójkąt 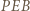 jest równoramienny.
jest równoramienny.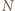 będzie środkiem odcinka
będzie środkiem odcinka 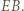 Skoro
Skoro 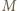 jest środkiem odcinka
jest środkiem odcinka 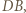 prosta
prosta 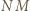 jest równoległa do prostej
jest równoległa do prostej 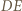 - która jest prostopadła do
- która jest prostopadła do 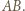 To znaczy, że prosta
To znaczy, że prosta 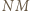 jest symetralną podstawy
jest symetralną podstawy 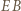 trójkąta równoramiennego
trójkąta równoramiennego 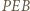 ; przechodzi więc przez punkt
; przechodzi więc przez punkt 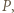 i mamy tezę
i mamy tezę 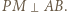
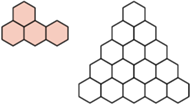
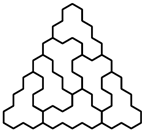
 oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei
oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei  -trójkątem nazwiemy trójkątny układ tworzony przez
-trójkątem nazwiemy trójkątny układ tworzony przez 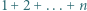 sześciokątów foremnych o boku
sześciokątów foremnych o boku 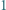 (na rysunku pokazano
(na rysunku pokazano 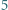 -trójkąt). Znaleźć wszystkie dodatnie liczby całkowite
-trójkąt). Znaleźć wszystkie dodatnie liczby całkowite 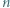 o tej własności, że z pewnej liczby płytek można ułożyć
o tej własności, że z pewnej liczby płytek można ułożyć 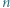 -trójkąt.
-trójkąt.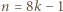 lub
lub 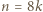 dla
dla 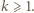
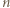 -trójkąt można ułożyć z płytek, to jest on złożony z podzielnej przez
-trójkąt można ułożyć z płytek, to jest on złożony z podzielnej przez 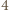 liczby sześciokątów foremnych o boku
liczby sześciokątów foremnych o boku 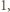 co oznacza, że liczba
co oznacza, że liczba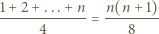
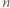 daje resztę 0 lub
daje resztę 0 lub 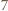 przy dzieleniu przez
przy dzieleniu przez 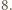
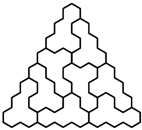
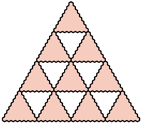
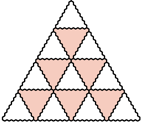
 -trójkąt oraz
-trójkąt oraz 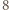 -trójkąt można ułożyć z płytek. Ponadto dla każdego
-trójkąt można ułożyć z płytek. Ponadto dla każdego 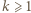 z
z 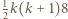 -trójkątów oraz
-trójkątów oraz 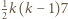 -trójkątów można ułożyć
-trójkątów można ułożyć 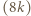 -trójkąt, a z
-trójkąt, a z 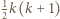
 -trójkątów oraz
-trójkątów oraz 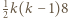 -trójkątów można ułożyć
-trójkątów można ułożyć 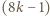 -trójkąt (rysunki 3 i 4;
-trójkąt (rysunki 3 i 4; 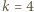 ).
). znajduje się wielokąt wypukły
znajduje się wielokąt wypukły  o polu większym od
o polu większym od 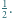 Wykazać, że wewnątrz wielokąta
Wykazać, że wewnątrz wielokąta 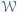 można wskazać odcinek o długości
można wskazać odcinek o długości  równoległy do boku kwadratu
równoległy do boku kwadratu 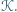
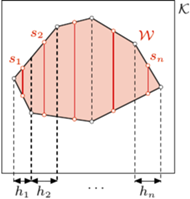
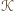 przez wszystkie wierzchołki wielokąta
przez wszystkie wierzchołki wielokąta 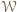 - dzielą one
- dzielą one 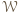 na pewną liczbę trapezów i trójkątów
na pewną liczbę trapezów i trójkątów 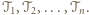 Niech
Niech 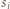 będzie odcinkiem łączącym środki tych boków wielokąta
będzie odcinkiem łączącym środki tych boków wielokąta 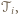 które nie są równoległe do poprowadzonych prostych, a
które nie są równoległe do poprowadzonych prostych, a 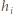 - wysokością
- wysokością 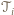 prostopadłą do
prostopadłą do 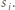 Wówczas
Wówczas![[𝒯i] = sihi](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/10x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-dm-66,57,43-FF,FF,FF.gif)
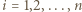 oraz
oraz![n [𝒲] = Q [𝒯 ], i 1 i](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/12x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-dm-66,57,43-FF,FF,FF.gif)
![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/13x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-im-66,57,43-FF,FF,FF.gif) oznacza pole figury
oznacza pole figury 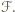 Zauważmy, że gdyby każdy z odcinków
Zauważmy, że gdyby każdy z odcinków 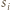 miał długość nie większą od
miał długość nie większą od 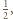 to uzyskalibyśmy nierówność
to uzyskalibyśmy nierówność![n n [𝒲] = Q sihi ⩽ 12Q hi⩽ 12, i 1 i 1](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/17x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-dm-66,57,43-FF,FF,FF.gif)
![1 [𝒲] > 2.](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/29/zm-1573/18x-ff85c30cb93a572ba81f1b5dc5d84dc2709e5266-im-66,57,43-FF,FF,FF.gif) Wobec tego dla pewnego
Wobec tego dla pewnego 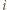 mamy
mamy 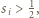 czyli
czyli 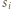 zawiera odcinek o postulowanej własności.
zawiera odcinek o postulowanej własności.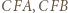 mają podstawy równe
mają podstawy równe 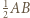 i wspólną wysokość z
i wspólną wysokość z 
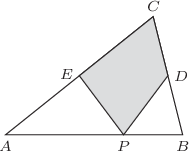
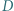 i
i 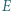 są środkami odpowiednio boków
są środkami odpowiednio boków 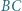 i
i 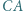 trójkąta
trójkąta 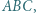 punkt
punkt 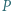 leży na boku
leży na boku 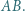 Wyznacz możliwe wartości
Wyznacz możliwe wartości ![CE] [A[PBDC].](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/8x-d6b862d2b936660f4e232be0352df6872ed9f71a-im-2C,6B,73-FF,FF,FF.gif)
![CE] [A[PBDC]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/1x-9b079c3bf7a5dc64ff2af43400eb31797dce6989-im-66,57,43-FF,FF,FF.gif) gdyż
gdyż ![C]=[PDB] [PD](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/2x-9b079c3bf7a5dc64ff2af43400eb31797dce6989-im-66,57,43-FF,FF,FF.gif) oraz
oraz ![[PEC]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-2/3x-9b079c3bf7a5dc64ff2af43400eb31797dce6989-im-66,57,43-FF,FF,FF.gif)
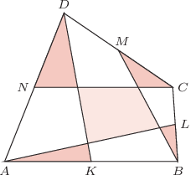
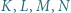 są środkami boków czworokąta wypukłego
są środkami boków czworokąta wypukłego 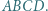 Wykaż, że suma pól ciemnych trójkątów równa jest polu jasnego czworokąta.
Wykaż, że suma pól ciemnych trójkątów równa jest polu jasnego czworokąta.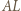 i
i 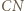 są środkowymi odpowiednio w trójkątach
są środkowymi odpowiednio w trójkątach 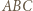 i
i 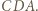 Stąd i z zadania 1 mamy
Stąd i z zadania 1 mamy ![1 ]=2[ABC][ABL] |](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-3/5x-af34f27462a93ab081e24def42194e47a65f46aa-im-66,57,43-FF,FF,FF.gif) Podobnie
Podobnie ![K]+[BDM]=12[ABCD].[BD](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-3/6x-af34f27462a93ab081e24def42194e47a65f46aa-im-66,57,43-FF,FF,FF.gif) Zatem
Zatem ![]=[BMDK], [ABL]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-3/7x-af34f27462a93ab081e24def42194e47a65f46aa-im-66,57,43-FF,FF,FF.gif) co, po odjęciu od obu stron ich części wspólnej, kończy dowód.
co, po odjęciu od obu stron ich części wspólnej, kończy dowód.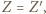 gdyż
gdyż 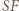 jest środkową w trójkącie
jest środkową w trójkącie 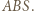 Analogicznie
Analogicznie 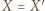 i
i 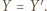 Ale także
Ale także 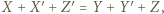 bo
bo 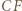 jest środkową trójkąta
jest środkową trójkąta 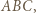 co wobec powyższego daje
co wobec powyższego daje 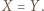 Podobnie
Podobnie 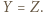
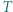 należy do wnętrza trójkąta
należy do wnętrza trójkąta 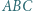 oraz
oraz 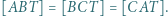 Wykaż, że
Wykaż, że 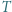 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 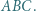
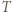 leży wewnątrz lub na brzegu trójkąta
leży wewnątrz lub na brzegu trójkąta 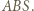 Wtedy jeśli
Wtedy jeśli 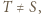 to
to 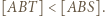 Z treści zadania wynika, że
Z treści zadania wynika, że 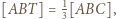 a z zadania 4 wiemy, że
a z zadania 4 wiemy, że ![|[ABS]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-5/6x-4d0410538dd904420200c91e9bf3d520281bcf04-im-66,57,43-FF,FF,FF.gif) Stąd
Stąd 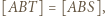 więc
więc 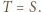
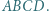 Punkty
Punkty 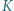 i
i 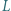 są środkami boków
są środkami boków 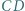 i
i 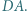 Proste
Proste 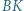 i
i 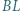 przecinają przekątną
przecinają przekątną 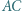 odpowiednio w punktach
odpowiednio w punktach 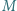 i
i 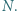 Wykaż, że
Wykaż, że ![1 ]+[BMN]+[CKM]=3[ABCD] |[ALN](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/11x-a985b0af3fbf2b8f27676b5a2afc831fe04a782f-im-2C,6B,73-FF,FF,FF.gif) oraz że
oraz że 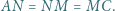
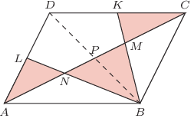
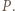 Odcinki
Odcinki 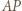 i
i 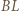 oraz
oraz 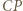 i
i 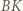 są zatem środkowymi odpowiednio w trójkątach
są zatem środkowymi odpowiednio w trójkątach 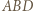 i
i 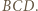 Trójkąty te mają pola równe
Trójkąty te mają pola równe ![1[ABCD] 2](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/8x-2283c17e109d15591b0d245c4473eb753c39dc9e-im-66,57,43-FF,FF,FF.gif) i na mocy zadania 4 ich środkowe dzielą każdy z nich na sześć trójkątów o równych polach. Stąd
i na mocy zadania 4 ich środkowe dzielą każdy z nich na sześć trójkątów o równych polach. Stąd ![12111 ]+[BMN]+[CKM]=(6+6+6)⋅2[ABCD]=3[ABCD] [ALN .](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/9x-2283c17e109d15591b0d245c4473eb753c39dc9e-im-66,57,43-FF,FF,FF.gif) Ponadto
Ponadto 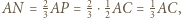 podobnie
podobnie 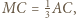 więc też
więc też 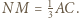
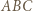 o
o 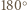 wokół punktu
wokół punktu 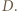 Boki trójkąta
Boki trójkąta 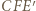 mają długości
mają długości 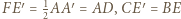 oraz
oraz 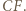
 Obróćmy trójkąt
Obróćmy trójkąt  o
o  wokół punktu
wokół punktu 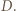 Trójkąt
Trójkąt 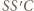 ma wówczas boki o długościach
ma wówczas boki o długościach 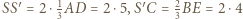 oraz
oraz 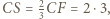 jest więc prostokątny. Stąd jego pole równe jest
jest więc prostokątny. Stąd jego pole równe jest 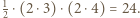 Jednocześnie na mocy zadania 4 wiemy, że pole to równe jest
Jednocześnie na mocy zadania 4 wiemy, że pole to równe jest 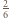 pola trójkąta
pola trójkąta 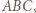 zatem
zatem ![|[ABC] .](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-8/11x-8282951b1e1d6cfb55ae221251f78463d5dae986-im-66,57,43-FF,FF,FF.gif)
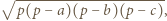
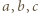 to boki,
to boki, 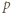 - połowa obwodu.
- połowa obwodu.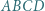 podstawa
podstawa 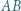 jest dwa razy dłuższa od podstawy
jest dwa razy dłuższa od podstawy 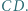 Punkt
Punkt 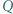 jest środkiem przekątnej
jest środkiem przekątnej 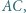 a prosta
a prosta 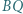 przecina bok
przecina bok 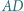 w punkcie
w punkcie 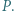 Wyznacz
Wyznacz ![[PQCD]](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-9/9x-59beed1787f722ef146fe03a4f1f01fb55efe3fb-im-2C,6B,73-FF,FF,FF.gif)