Zadanie ZM-19.06-KPO-8
o zadaniu...
- Publikacja w Delcie: czerwiec 2019
- Publikacja elektroniczna: 31 maja 2019
W czworościanie 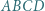 wszystkie wewnętrzne kąty dwuścienne są ostre. Punkt
wszystkie wewnętrzne kąty dwuścienne są ostre. Punkt 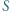 leży wewnątrz tego czworościanu, a jego odległość od każdej z płaszczyzn
leży wewnątrz tego czworościanu, a jego odległość od każdej z płaszczyzn 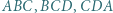 i
i 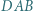 jest większa niż
jest większa niż 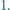 Dowieść, że przynajmniej dwa spośród odcinków
Dowieść, że przynajmniej dwa spośród odcinków 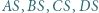 mają długość większą niż
mają długość większą niż 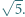

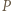 na płaszczyznę
na płaszczyznę 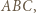 otrzymamy punkt
otrzymamy punkt 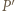 leżący wewnątrz trójkąta
leżący wewnątrz trójkąta 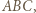 którego odległość od każdego z boków tego trójkąta jest większa od
którego odległość od każdego z boków tego trójkąta jest większa od 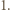 Któryś z kątów trójkąta
Któryś z kątów trójkąta 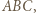 powiedzmy kąt
powiedzmy kąt 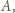 ma miarę nieprzekraczającą
ma miarę nieprzekraczającą 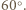 Stąd
Stąd 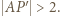 Mamy też
Mamy też 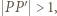 więc z twierdzenia Pitagorasa dla trójkąta
więc z twierdzenia Pitagorasa dla trójkąta 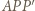 otrzymamy
otrzymamy 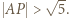 Powtarzając to rozumowanie dla płaszczyzny
Powtarzając to rozumowanie dla płaszczyzny 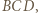 otrzymamy tezę.
otrzymamy tezę.