Zadanie ZM-1503
o zadaniu...
- Publikacja w Delcie: sierpień 2016
- Publikacja elektroniczna: 31 lipca 2016
Punkty 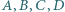 leżą kolejno na okręgu
leżą kolejno na okręgu 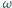 w taki sposób, że cięciwy
w taki sposób, że cięciwy 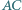 i
i 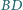 przecinają się pod kątem prostym. Obliczyć promień
przecinają się pod kątem prostym. Obliczyć promień  okręgu
okręgu 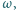 jeśli cięciwy
jeśli cięciwy 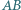 i
i 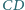 mają odpowiednio długości
mają odpowiednio długości 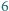 i
i 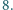
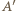 będzie punktem symetrycznym do
będzie punktem symetrycznym do 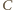 względem środka okręgu. Wówczas
względem środka okręgu. Wówczas 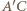 jest średnicą okręgu, więc cięciwa
jest średnicą okręgu, więc cięciwa 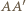 jest prostopadła do odcinka
jest prostopadła do odcinka 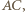 a więc również równoległa do odcinka
a więc również równoległa do odcinka 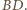 W takim razie
W takim razie 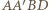 jest trapezem równoramiennym, w szczególności
jest trapezem równoramiennym, w szczególności 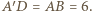 Z twierdzenia Pitagorasa dla trójkąta
Z twierdzenia Pitagorasa dla trójkąta 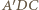 otrzymujemy
otrzymujemy 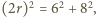 a stąd
a stąd 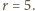
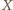 i
i 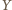 oznaczają odpowiednio punkty przecięcia prostych
oznaczają odpowiednio punkty przecięcia prostych 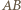 z
z 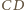 oraz
oraz 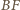 z
z 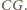 Wówczas każdy z punktów
Wówczas każdy z punktów 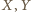 należy do obu płaszczyzn rozważanych powyżej ścian, a więc też do ich wspólnej prostej. Jednak punkty
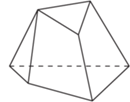
należy do obu płaszczyzn rozważanych powyżej ścian, a więc też do ich wspólnej prostej. Jednak punkty 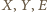 nie są współliniowe, zatem rysunek nie przedstawia wielościanu.
nie są współliniowe, zatem rysunek nie przedstawia wielościanu.
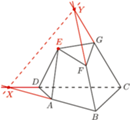
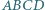 przecięto płaszczyzną, uzyskując w przekroju czworokąt
przecięto płaszczyzną, uzyskując w przekroju czworokąt 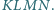 Na rysunku obok wyznacz punkt
Na rysunku obok wyznacz punkt  posługując się jedynie linijką.
posługując się jedynie linijką.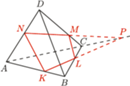
 punkt przecięcia prostych
punkt przecięcia prostych 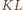 i
i 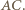 Punkt ten leży w płaszczyźnie przekroju, zatem leży w niej też prosta
Punkt ten leży w płaszczyźnie przekroju, zatem leży w niej też prosta  Stąd brakujący punkt
Stąd brakujący punkt  to punkt przecięcia prostych
to punkt przecięcia prostych 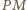 i
i 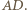
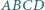 podstawa
podstawa 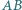 ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt
ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt 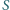 jest wierzchołkiem ostrosłupa o podstawie
jest wierzchołkiem ostrosłupa o podstawie  w którym
w którym  Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.
Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.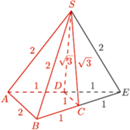
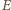 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 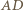 i
i 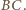 Z kształtu trapezu
Z kształtu trapezu 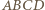 wynika, że
wynika, że 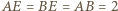 oraz że jego pole to
oraz że jego pole to 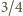 pola trójkąta
pola trójkąta 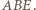
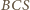 wnioskujemy, że jest on połową trójkąta równobocznego o krawędzi 2. Ponieważ
wnioskujemy, że jest on połową trójkąta równobocznego o krawędzi 2. Ponieważ 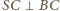 oraz
oraz 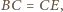 więc
więc 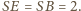
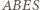 jest foremny o krawędzi 2. Jego objętość jest zatem 8-krotnie większa od objętości czworościanu foremnego o krawędzi 1, więc szukany stosunek objętości równy jest
jest foremny o krawędzi 2. Jego objętość jest zatem 8-krotnie większa od objętości czworościanu foremnego o krawędzi 1, więc szukany stosunek objętości równy jest 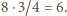
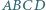 nie będący trapezem. Proste
nie będący trapezem. Proste 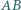 i
i 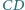 przecinają się w punkcie
przecinają się w punkcie  Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu
Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu  od płaszczyzny podstawy ostrosłupa.
od płaszczyzny podstawy ostrosłupa.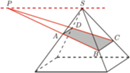
 leży w płaszczyźnie przedniej ściany ostrosłupa z rysunku, a prosta
leży w płaszczyźnie przedniej ściany ostrosłupa z rysunku, a prosta 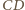 w płaszczyźnie tylnej ściany, więc punkt
w płaszczyźnie tylnej ściany, więc punkt 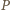 należy do obydwu tych płaszczyzn. Ich częścią wspólną jest prosta równoległa do podstawy ostrosłupa (gdyż jest on prawidłowy) i przechodząca przez wierzchołek
należy do obydwu tych płaszczyzn. Ich częścią wspólną jest prosta równoległa do podstawy ostrosłupa (gdyż jest on prawidłowy) i przechodząca przez wierzchołek 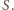 Stąd jedyną wartością, jaką może przyjąć odległość punktu
Stąd jedyną wartością, jaką może przyjąć odległość punktu 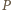 od płaszczyzny podstawy, jest wysokość ostrosłupa równa
od płaszczyzny podstawy, jest wysokość ostrosłupa równa 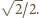
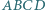 i krawędziach bocznych
i krawędziach bocznych 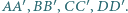 Wyznacz miarę kąta dwuściennego między płaszczyznami
Wyznacz miarę kąta dwuściennego między płaszczyznami 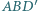 i
i 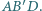
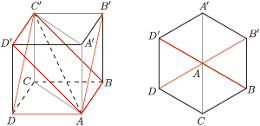
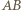 i
i 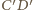 są równoległe, leżą więc w jednej płaszczyźnie
są równoległe, leżą więc w jednej płaszczyźnie 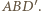 Stąd punkt
Stąd punkt 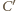 też do niej należy; podobnie należy on także do
też do niej należy; podobnie należy on także do 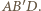 Punkty
Punkty 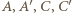 również leżą w jednej płaszczyźnie.
również leżą w jednej płaszczyźnie. i każda z nich zawiera inną z trzech krawędzi wychodzących z wierzchołka
i każda z nich zawiera inną z trzech krawędzi wychodzących z wierzchołka 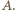 Oznacza to, że płaszczyzny te tworzą równe kąty dwuścienne, czyli kąty po
Oznacza to, że płaszczyzny te tworzą równe kąty dwuścienne, czyli kąty po 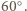
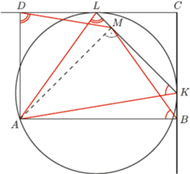
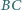 i
i 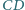 prostokąta
prostokąta 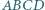 są styczne odpowiednio w punktach
są styczne odpowiednio w punktach 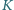 i
i 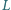 do okręgu przechodzącego przez
do okręgu przechodzącego przez 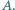 Na odcinku
Na odcinku 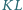 leży taki punkt
leży taki punkt 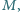 że proste
że proste 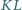 i
i 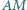 są prostopadłe. Obliczyć pole prostokąta
są prostopadłe. Obliczyć pole prostokąta 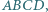 wiedząc, że odcinek
wiedząc, że odcinek 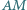 ma długość
ma długość 
 jest prostopadła do
jest prostopadła do  więc jest nachylona do boków prostokąta pod kątem
więc jest nachylona do boków prostokąta pod kątem 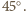 Ponadto kąt środkowy oparty na cięciwie
Ponadto kąt środkowy oparty na cięciwie 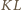 jest prosty, a stąd
jest prosty, a stąd 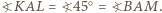
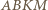 jest opisany na okręgu o średnicy
jest opisany na okręgu o średnicy 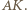 W takim razie kąty
W takim razie kąty 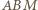 i
i 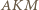 są równe.
są równe.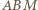 i
i 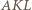 są podobne. Analogicznie trójkąty
są podobne. Analogicznie trójkąty 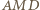 i
i 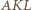 są podobne. W takim razie mamy podobieństwo trójkątów
są podobne. W takim razie mamy podobieństwo trójkątów 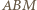 i
i 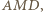 a stąd
a stąd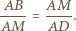
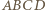 jest równe
jest równe 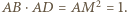
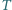 rozcięto wzdłuż odcinka na dwa trójkąty
rozcięto wzdłuż odcinka na dwa trójkąty 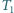 i
i 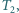 a trójkąt
a trójkąt 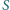 - na trójkąty
- na trójkąty 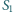 i
i 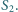 Okazało się, że trójkąt
Okazało się, że trójkąt 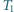 jest przystający do trójkąta
jest przystający do trójkąta 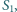 a trójkąt
a trójkąt 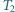 jest przystający do trójkąta
jest przystający do trójkąta 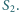 Czy wynika z tego, że trójkąty
Czy wynika z tego, że trójkąty 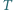 i
i 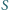 są przystające?
są przystające?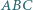 i
i 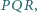 przy czym
przy czym 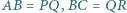 oraz
oraz 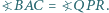 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?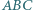 i
i 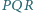 mają równe pola oraz
mają równe pola oraz 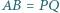 i
i 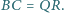 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?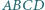 i
i 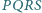 mają równe pola oraz
mają równe pola oraz 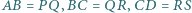 i
i 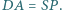 Czy wynika z tego, że czworokąty te są przystające?
Czy wynika z tego, że czworokąty te są przystające?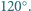 Czy wynika z tego, że jest on foremny?
Czy wynika z tego, że jest on foremny? leży wewnątrz trójkąta ostrokątnego
leży wewnątrz trójkąta ostrokątnego 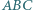 oraz
oraz 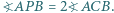 Czy wynika z tego, że
Czy wynika z tego, że 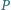 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 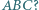
 boków. Czy wynika z tego, że ściana ta graniczy z
boków. Czy wynika z tego, że ściana ta graniczy z  innymi ścianami tego wielościanu?
innymi ścianami tego wielościanu?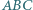 kąt przy wierzchołku
kąt przy wierzchołku 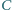 ma miarę
ma miarę 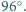 Wewnątrz trójkąta leży taki punkt
Wewnątrz trójkąta leży taki punkt 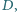 że
że 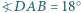 i
i 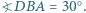 Wyznaczyć miarę kąta
Wyznaczyć miarę kąta 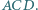
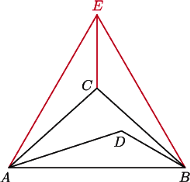
 że punkt
że punkt  leży w jego wnętrzu. Wówczas punkty
leży w jego wnętrzu. Wówczas punkty 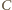 i
i 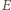 leżą na symetralnej odcinka
leżą na symetralnej odcinka 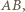 więc
więc 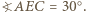 Ponadto
Ponadto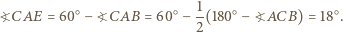
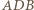 i
i 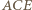 są przystające, w szczególności
są przystające, w szczególności 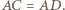 Stąd łatwo otrzymujemy
Stąd łatwo otrzymujemy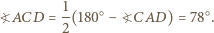
 trójkąta
trójkąta 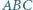 leżą punkty
leżą punkty  w których okręgi dopisane do trójkąta są styczne do tych boków. Niech
w których okręgi dopisane do trójkąta są styczne do tych boków. Niech 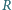 i
i  będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów
będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów 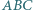 i
i 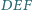 wynosi
wynosi 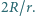
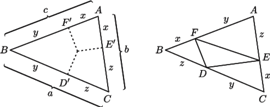
 są położone na bokach
są położone na bokach  symetrycznie (względem środków owych boków) do punktów
symetrycznie (względem środków owych boków) do punktów  w których okrąg wpisany jest do boków styczny. Przyjmijmy oznaczenia:
w których okrąg wpisany jest do boków styczny. Przyjmijmy oznaczenia: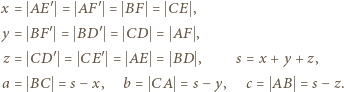
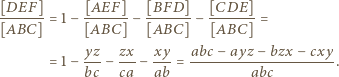
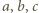 przez
przez 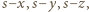 otrzymujemy po krótkim rachunku wzór
otrzymujemy po krótkim rachunku wzór![EF] [D----- 2xyz- [ABC]= abc .](/math/temat/matematyka/geometria/planimetria/zadania/2016/05/01/zm-k44-721/4x-a024003798da1c7ac2b5aca0bcab255a844a5624-dm-66,57,43-FF,FF,FF.gif)
 i
i 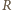 to promienie okręgów wpisanego i opisanego):
to promienie okręgów wpisanego i opisanego):![[ABC]](/math/temat/matematyka/geometria/planimetria/zadania/2016/05/01/zm-k44-721/7x-a024003798da1c7ac2b5aca0bcab255a844a5624-dm-66,57,43-FF,FF,FF.gif)
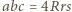 oraz
oraz 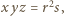 które po wprowadzeniu do równości
które po wprowadzeniu do równości 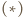 dają tezę zadania.
dają tezę zadania.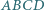 wpisanego w okrąg o środku
wpisanego w okrąg o środku 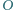 przecinają się w punkcie
przecinają się w punkcie 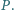 Niech
Niech 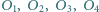 będą środkami okręgów opisanych odpowiednio na trójkątach
będą środkami okręgów opisanych odpowiednio na trójkątach 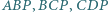 i
i 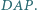 Wykazać, że proste
Wykazać, że proste 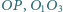 i
i 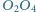 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
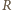 będzie punktem przecięcia prostej
będzie punktem przecięcia prostej 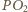 z prostą
z prostą 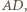 a
a 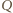 różnym od
różnym od 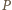 punktem przecięcia tej prostej z okręgiem opisanym na trójkącie
punktem przecięcia tej prostej z okręgiem opisanym na trójkącie 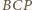 (rysunek). Wówczas
(rysunek). Wówczas 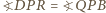 oraz
oraz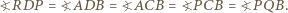
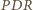 i
i 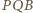 są podobne, w szczególności
są podobne, w szczególności 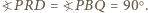 Stąd prosta
Stąd prosta 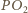 jest prostopadła do
jest prostopadła do 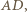 a więc również równoległa do
a więc również równoległa do 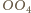 - symetralnej
- symetralnej 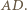 Analogicznie proste
Analogicznie proste 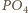 i
i 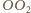 są równoległe. W takim razie odcinki
są równoległe. W takim razie odcinki 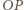 i
i 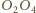 przecinają się w połowie jako przekątne równoległoboku.
przecinają się w połowie jako przekątne równoległoboku.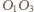 przechodzi przez środek odcinka
przechodzi przez środek odcinka 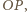 co daje tezę.
co daje tezę.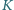 i
i 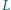 są środkami odpowiednio boków
są środkami odpowiednio boków 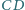 i
i 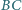 równoległoboku
równoległoboku 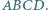 Udowodnij, że odcinki
Udowodnij, że odcinki 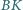 i
i 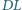 przecinają się na przekątnej
przecinają się na przekątnej 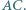

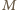 będzie punktem przecięcia przekątnych danego równoległoboku. Wówczas
będzie punktem przecięcia przekątnych danego równoległoboku. Wówczas 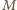 jest środkiem odcinka
jest środkiem odcinka 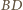 i odcinki
i odcinki 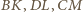 przecinają się w jednym punkcie jako środkowe trójkąta
przecinają się w jednym punkcie jako środkowe trójkąta 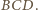
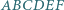 jest wpisany w okrąg i
jest wpisany w okrąg i 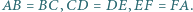 Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
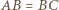 wynika, że punkt
wynika, że punkt 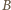 jest środkiem łuku
jest środkiem łuku 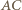 danego okręgu i kąty wpisane
danego okręgu i kąty wpisane 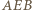 i
i 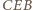 są równe. Prosta
są równe. Prosta 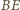 jest więc dwusieczną kąta
jest więc dwusieczną kąta 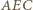 w trójkącie
w trójkącie 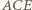 ; analogicznie proste
; analogicznie proste 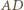 i
i 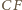 są dwusiecznymi pozostałych kątów tego trójkąta.
są dwusiecznymi pozostałych kątów tego trójkąta.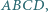 w którym
w którym 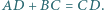 Dwusieczne kątów
Dwusieczne kątów 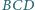 i
i 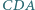 przecinają się w punkcie
przecinają się w punkcie 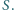 Udowodnij, że
Udowodnij, że 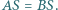

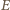 będzie takim punktem boku
będzie takim punktem boku 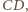 że
że 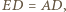 wtedy
wtedy 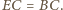 Wówczas punkty
Wówczas punkty 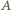 i
i 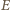 są symetryczne względem dwusiecznej kąta
są symetryczne względem dwusiecznej kąta 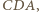 zatem prosta
zatem prosta 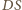 jest symetralną odcinka
jest symetralną odcinka 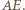 Analogicznie prosta
Analogicznie prosta 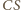 jest symetralną odcinka
jest symetralną odcinka 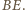 Symetralne boków trójkąta
Symetralne boków trójkąta 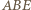 przecinają się w punkcie
przecinają się w punkcie 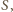 a stąd
a stąd 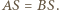
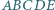 są równe. Symetralne odcinków
są równe. Symetralne odcinków 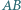 i
i  przecinają się w punkcie
przecinają się w punkcie 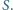 Wykaż, że proste
Wykaż, że proste 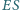 i
i 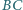 są prostopadłe.
są prostopadłe.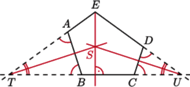
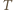 i
i 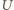 będą punktami przecięcia prostej
będą punktami przecięcia prostej 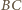 odpowiednio z prostymi
odpowiednio z prostymi 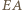 i
i 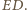 Wobec równości kątów, trójkąty
Wobec równości kątów, trójkąty 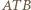 i
i 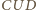 są równoramienne i podobne, a stąd
są równoramienne i podobne, a stąd 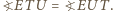 Symetralna boku
Symetralna boku 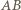 jest jednocześnie dwusieczną kąta przy wierzchołku
jest jednocześnie dwusieczną kąta przy wierzchołku 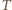 w trójkącie
w trójkącie 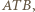 a więc także w trójkącie
a więc także w trójkącie 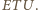 Podobnie symetralna odcinka
Podobnie symetralna odcinka 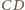 jest dwusieczną kąta
jest dwusieczną kąta 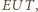 zatem
zatem 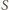 jest punktem przecięcia dwusiecznych trójkąta równoramiennego
jest punktem przecięcia dwusiecznych trójkąta równoramiennego 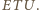 Dwusieczna
Dwusieczna 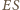 jest więc prostopadła do podstawy
jest więc prostopadła do podstawy 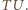
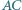 i
i 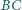 trójkąta
trójkąta 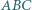 zbudowano, na zewnątrz, kwadraty
zbudowano, na zewnątrz, kwadraty 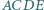 i
i 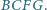 Udowodnij, że proste
Udowodnij, że proste 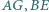 oraz wysokość
oraz wysokość 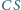 trójkąta
trójkąta 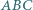 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.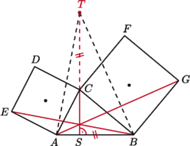
 o
o 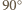 wokół środka tak, by punkt
wokół środka tak, by punkt 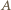 przeszedł na punkt
przeszedł na punkt 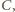 natomiast kwadrat
natomiast kwadrat 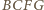 o
o 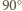 wokół swojego środka tak, by punkt
wokół swojego środka tak, by punkt 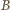 przeszedł na punkt
przeszedł na punkt 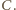 Przy obydwu tych obrotach odcinek
Przy obydwu tych obrotach odcinek 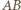 przechodzi na ten sam odcinek o końcu w punkcie
przechodzi na ten sam odcinek o końcu w punkcie 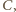 prostopadły do
prostopadły do 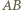 i równy
i równy 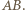 Nazwijmy drugi jego koniec
Nazwijmy drugi jego koniec 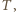 wówczas punkty
wówczas punkty 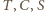 są współliniowe.
są współliniowe.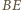 przechodzi na
przechodzi na 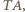 stąd
stąd 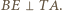 Przy drugim obrocie odcinek
Przy drugim obrocie odcinek 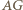 przechodzi na
przechodzi na 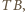 zatem
zatem 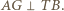 Wobec tego proste
Wobec tego proste 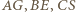 są wysokościami trójkąta
są wysokościami trójkąta 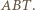
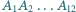 przekątne
przekątne 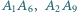 i
i 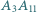 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.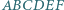 jest równa
jest równa 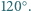 Udowodnij, że symetralne odcinków
Udowodnij, że symetralne odcinków 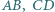 i
i 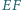 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.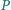 leży wewnątrz trójkąta
leży wewnątrz trójkąta 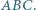 Punkty
Punkty 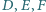 to punkty symetryczne do punktu
to punkty symetryczne do punktu 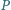 odpowiednio względem prostych
odpowiednio względem prostych 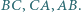 Wykaż, że jeśli trójkąt
Wykaż, że jeśli trójkąt 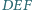 jest równoboczny, to proste
jest równoboczny, to proste 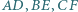 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.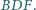
 jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że
jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że 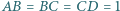 oraz
oraz 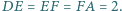
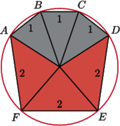
 jak na rysunku.
jak na rysunku.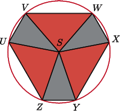
 oznacza środek okręgu opisanego na sześciokącie
oznacza środek okręgu opisanego na sześciokącie  Z przystawania czworokątów
Z przystawania czworokątów 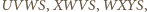
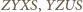 i
i 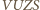 wiemy, że kąty wewnętrzne sześciokąta są przystające, mają więc po
wiemy, że kąty wewnętrzne sześciokąta są przystające, mają więc po 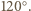 Z twierdzenia cosinusów dla trójkąta
Z twierdzenia cosinusów dla trójkąta 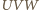 otrzymujemy
otrzymujemy 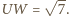 Trójkąt
Trójkąt 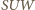 jest trójkątem równoramiennym o kącie
jest trójkątem równoramiennym o kącie 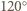 w wierzchołku
w wierzchołku 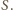 Stąd możemy obliczyć szukany promień, równy
Stąd możemy obliczyć szukany promień, równy 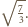
 Proste zawierające dwusieczne kątów wewnętrznych
Proste zawierające dwusieczne kątów wewnętrznych 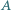 i
i 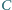 przecinają się w punkcie
przecinają się w punkcie 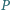 leżącym wewnątrz czworokąta
leżącym wewnątrz czworokąta 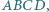 a proste zawierające dwusieczne kątów wewnętrznych
a proste zawierające dwusieczne kątów wewnętrznych 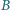 i
i 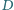 przecinają się w punkcie
przecinają się w punkcie 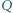 na zewnątrz czworokąta. Udowodnij, że jeżeli kąt
na zewnątrz czworokąta. Udowodnij, że jeżeli kąt 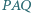 jest prosty, to również kąt
jest prosty, to również kąt 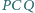 jest prosty.
jest prosty.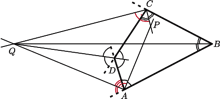
 jest prosty, to
jest prosty, to  jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta  czworokąta. Z kolei aby dowieść, że kąt
czworokąta. Z kolei aby dowieść, że kąt 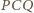 jest prosty, wystarczy wykazać, że
jest prosty, wystarczy wykazać, że 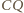 jest dwusieczną kąta przyległego do kąta
jest dwusieczną kąta przyległego do kąta 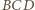 czworokąta.
czworokąta.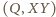 odległość punktu
odległość punktu 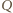 od prostej
od prostej 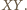 Zachodzą równości
Zachodzą równości 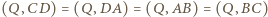 oraz
oraz 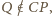 co kończy dowód.
co kończy dowód.