Zadanie ZM-1623
o zadaniu...
- Publikacja w Delcie: grudzień 2019
- Publikacja elektroniczna: 30 listopada 2019
Dany jest kwadrat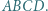 
Punkty 
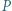i 
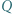leżące odpowiednio wewnątrz trójkątów 
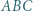i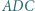 
mają tę własność, że 
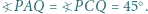Wykazać, że
gdzie ![[ℱ]](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/8x-36c19e6efa8cca90b4ecde58a9ea9c818585cc21-im-2C,6B,73-FF,FF,FF.gif)
oznacza pole figury 
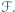
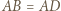oraz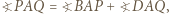 
to istnieje punkt jednocześnie symetryczny do 
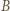względem 
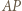i do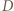 
względem 
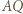; nazwijmy go 
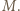Skoro ![|[ABP P]](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/8x-9b94bf9272daebe741e8a2a4d8c739547e0d607b-im-66,57,43-FF,FF,FF.gif)
oraz ![QQ]], |[AD](/math/temat/matematyka/geometria/planimetria/zadania/2019/11/29/zm-1623/9x-9b94bf9272daebe741e8a2a4d8c739547e0d607b-im-66,57,43-FF,FF,FF.gif)
to lewa strona dowodzonej równości przybiera postać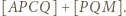 
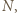jednocześnie symetryczny do 
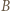względem 
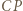oraz do 
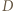względem 
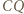i podobnie prawą stronę dowodzonej równości można przepisać jako 
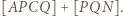Do zakończenia rozwiązania wystarczy zauważyć, że trójkąty 
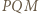oraz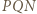 
są przystające (cecha bok-bok-bok).