Twierdzenie Menelaosa»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Twierdzenie Menelaosa
- Publikacja w Delcie: marzec 2011
- Publikacja elektroniczna: 02-03-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (71 KB)
Wykaż, że złożenie jednokładności o środku
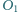 i skali
i skali
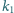 z jednokładnością o środku
z jednokładnością o środku
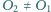 i skali
i skali
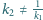 jest
jednokładnością o środku na prostej
jest
jednokładnością o środku na prostej
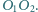
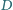
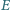
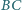
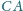
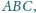
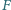
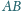
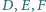
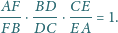
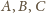 na prostą
na prostą
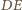 i zastosuj twierdzenie
Talesa.
i zastosuj twierdzenie
Talesa.
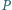 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
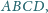 przy czym
środek odcinka
przy czym
środek odcinka
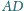 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
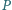 i
i
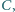 a środek odcinka
a środek odcinka
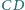 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
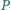 i
i
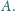 Punkt
Punkt
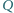 jest środkiem odcinka
jest środkiem odcinka
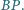 Wykazać, że
Wykazać, że
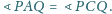
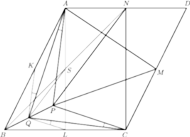
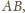
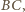
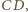
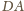 odpowiednio przez
odpowiednio przez
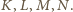 W myśl założenia,
W myśl założenia,
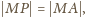
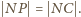 Niech
Niech
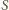 będzie wspólnym środkiem przekątnych
będzie wspólnym środkiem przekątnych
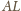 i
i
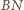 równoległoboku
równoległoboku
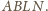 Odcinek
Odcinek
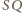 łączy środki
dwóch boków trójkąta
łączy środki
dwóch boków trójkąta
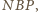 więc
więc
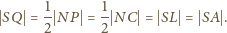
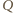 leży na okręgu o średnicy
leży na okręgu o średnicy
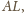 wobec czego kąt
wobec czego kąt
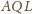 jest prosty. Analogicznie, kąt
jest prosty. Analogicznie, kąt
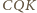 jest prosty. Stąd
wynika, że
jest prosty. Stąd
wynika, że
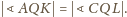 Punkty
Punkty
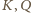 są środkami
dwóch boków trójkąta
są środkami
dwóch boków trójkąta
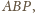 więc
więc
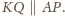 Analogicznie,
Analogicznie,
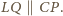 Stąd, ostatecznie,
Stąd, ostatecznie,
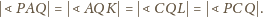
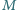 jest środkiem boku
jest środkiem boku
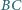 trójkąta ostrokątnego
trójkąta ostrokątnego
 Punkt
Punkt
 leży na boku
leży na boku
 i spełnia warunek
i spełnia warunek
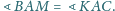 Na odcinku
Na odcinku
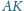 wybrano taki punkt
wybrano taki punkt
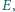 że
że
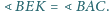 Dowieść, że
Dowieść, że
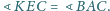
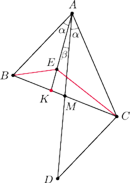
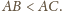 Oznaczmy
Oznaczmy
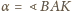 oraz
oraz
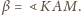 Niech
Niech
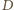 będzie takim punktem, że czworokąt
będzie takim punktem, że czworokąt
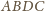 jest
równoległobokiem (
jest
równoległobokiem (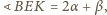 więc
więc
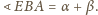 Oznacza to, że
Oznacza to, że
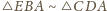 i
i
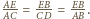 Ponadto
Ponadto
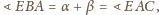 co oznacza, że
co oznacza, że
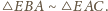 Stąd
Stąd
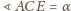 i
i
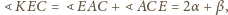 co należało
wykazać. Zauważamy jeszcze, że gdy
co należało
wykazać. Zauważamy jeszcze, że gdy
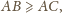 rozumowanie jest
analogiczne.
rozumowanie jest
analogiczne.
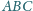 obrano punkt
obrano punkt
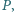 taki że
taki że
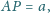

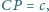 gdzie
gdzie
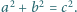 Wyznaczyć długość boku trójkąta
Wyznaczyć długość boku trójkąta
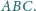
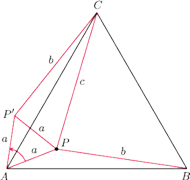
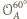 oraz punkt
oraz punkt
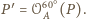 Zauważmy, że
Zauważmy, że
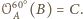 Tak więc
Tak więc
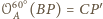 i w szczególności
i w szczególności
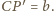 Trójkąt
Trójkąt
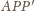 jest równoboczny, więc
jest równoboczny, więc
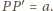 Z założeń wynika, iż
Z założeń wynika, iż
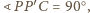 czyli
czyli
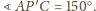 Stosując twierdzenie kosinusów
do trójkąta
Stosując twierdzenie kosinusów
do trójkąta
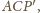 uzyskujemy
uzyskujemy
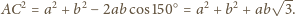
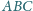 i
i
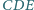 (mające wspólny wierzchołek
(mające wspólny wierzchołek
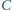 ) oraz punkty
) oraz punkty
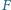 i
i
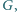 takie
że
takie
że
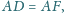
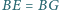 i
i
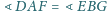 (jako kąty
skierowane). Wykazać, że trójkąt
(jako kąty
skierowane). Wykazać, że trójkąt
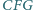 jest równoboczny.
jest równoboczny.
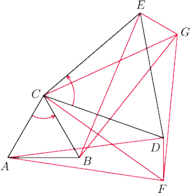
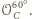 Zauważmy, że
Zauważmy, że
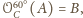
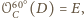 czyli
czyli
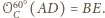 Stąd w szczególności
Stąd w szczególności
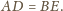 Na podstawie założeń (
Na podstawie założeń (
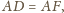
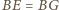 oraz
oraz
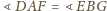 ) trójkąty
) trójkąty
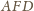 i
i
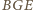 są przystające.
Tak więc
są przystające.
Tak więc
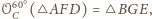 czyli
czyli
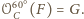
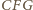 jest zatem równoboczny.
jest zatem równoboczny.
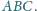 Rozważamy wszystkie takie
trójkąty równoboczne
Rozważamy wszystkie takie
trójkąty równoboczne
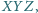 że punkty
że punkty
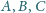 są punktami
wewnętrznymi odcinków
są punktami
wewnętrznymi odcinków
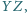
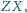
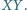 Dowieść, że
środki ciężkości wszystkich rozważanych trójkątów leżą na jednym
okręgu.
Dowieść, że
środki ciężkości wszystkich rozważanych trójkątów leżą na jednym
okręgu.
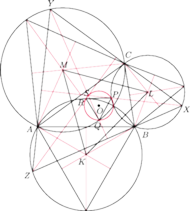
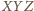 spełniający warunki zadania. Niech
spełniający warunki zadania. Niech
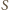 będzie jego środkiem ciężkości. Zauważmy, że bok
będzie jego środkiem ciężkości. Zauważmy, że bok
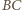 jest
widziany z punktu
jest
widziany z punktu
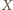 pod kątem
pod kątem
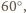 a więc
a więc
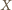 leży
na okręgu opisanym na trójkącie równobocznym zbudowanym zewnętrznie
na boku
leży
na okręgu opisanym na trójkącie równobocznym zbudowanym zewnętrznie
na boku
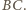 Analogicznie
Analogicznie
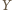 i
i
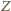 leżą na okręgach
opisanych na trójkątach równobocznych zbudowanych odpowiednio
na bokach
leżą na okręgach
opisanych na trójkątach równobocznych zbudowanych odpowiednio
na bokach
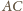 i
i
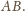
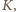
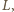
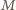 kolejne środki tych okręgów.
Z twierdzenia Napoleona (patrz np. Delta 6/2004) wynika, że trójkąt
kolejne środki tych okręgów.
Z twierdzenia Napoleona (patrz np. Delta 6/2004) wynika, że trójkąt
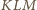 jest równoboczny. Niech
jest równoboczny. Niech
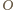 oznacza jego środek
ciężkości. Proste
oznacza jego środek
ciężkości. Proste
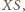
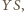
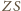 (jako dwusieczne kątów
wewnętrzych trójkąta
(jako dwusieczne kątów
wewnętrzych trójkąta
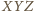 ) przecinają w połowie krótsze łuki
) przecinają w połowie krótsze łuki
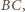
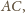
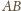 narysowanych okręgów. Środki tych
łuków oznaczmy kolejno przez
narysowanych okręgów. Środki tych
łuków oznaczmy kolejno przez
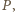
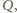
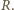 Zauważmy,
że
Zauważmy,
że
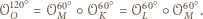
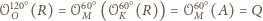
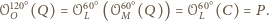
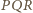 jest równoboczny
i jego środkiem ciężkości jest punkt
jest równoboczny
i jego środkiem ciężkości jest punkt
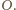 Pozostaje wykazać, iż
Pozostaje wykazać, iż
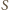 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie
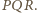 W tym celu,
ponieważ
W tym celu,
ponieważ
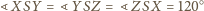
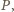
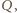
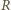 należą odpowiednio do prostych
należą odpowiednio do prostych
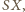
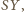
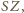 wystarczy zauważyć, że
wystarczy zauważyć, że
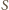 nie jest punktem
wewnętrznym trójkąta
nie jest punktem
wewnętrznym trójkąta
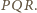 W przeciwnym razie, boki trójkąta
W przeciwnym razie, boki trójkąta
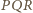 są widziane z punktu
są widziane z punktu
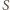 pod kątem
pod kątem
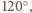 a więc
a więc
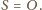 Wtedy punkt
Wtedy punkt
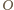 leży na zewnątrz okręgów opisanych
na „dobudowanych” na początku trójkątach równobocznych. Oznacza to, że
każdy z kątów
leży na zewnątrz okręgów opisanych
na „dobudowanych” na początku trójkątach równobocznych. Oznacza to, że
każdy z kątów
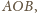
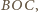
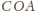 ma miarę mniejszą od
ma miarę mniejszą od
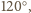 co jest niemożliwe.
co jest niemożliwe.
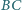 i
i
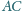 trójkąta
trójkąta
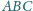 są jednocześnie bokami
kwadratów
są jednocześnie bokami
kwadratów
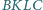 i
i
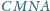 (leżących na zewnątrz trójkąta
(leżących na zewnątrz trójkąta
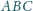 ). Punkty
). Punkty
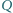 i
i
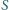 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
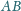 i
i
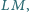 a
a
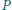 i
i
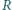 środkami kwadratów
środkami kwadratów
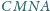 i
i
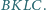 Wykazać, że czworokąt
Wykazać, że czworokąt
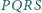 jest
kwadratem.
jest
kwadratem.
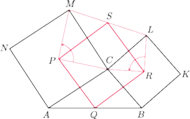
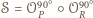 będące złożeniem dwóch
obrotów o kąt
będące złożeniem dwóch
obrotów o kąt
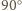 wokół punktów
wokół punktów
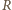 i
i
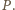 Na podstawie
Na podstawie
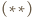
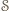 jest symetrią środkową względem punktu
jest symetrią środkową względem punktu
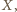 takiego
że
takiego
że
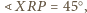
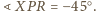 Z drugiej strony zauważmy,
że
Z drugiej strony zauważmy,
że
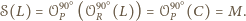
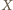 symetrii
symetrii
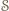 pokrywa się ze środkiem
pokrywa się ze środkiem
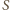 odcinka
odcinka
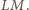 W szczególności
W szczególności
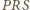 jest równoramiennym
trójkątem prostokątnym. Rozważając analogicznie złożenie obrotów
jest równoramiennym
trójkątem prostokątnym. Rozważając analogicznie złożenie obrotów
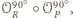 dowodzimy, że
dowodzimy, że
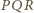 jest również równoramiennym
trójkątem prostokątnym. Tak więc czworokąt
jest również równoramiennym
trójkątem prostokątnym. Tak więc czworokąt
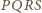 jest kwadratem.
jest kwadratem.
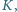
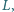
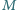 są środkami kwadratów zbudowanych
zewnętrznie na bokach
są środkami kwadratów zbudowanych
zewnętrznie na bokach
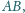
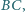
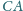 trójkąta
trójkąta
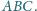 Wykazać, że
Wykazać, że
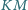 i
i
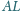 są prostopadłe,
są prostopadłe,
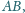
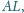
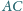 i
i
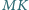 są
wierzchołkami kwadratu.
są
wierzchołkami kwadratu.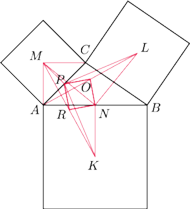
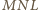 jest prostokątnym
trójkątem równoramiennym, przy czym
jest prostokątnym
trójkątem równoramiennym, przy czym
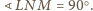 Zauważmy, że
Zauważmy, że
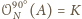 oraz
oraz
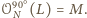 Tak więc
Tak więc
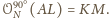 W szczególności odcinki
W szczególności odcinki
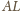 i
i
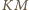 są prostopadłe.
są prostopadłe.
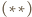 wiemy, że
wiemy, że
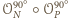 jest symetrią
środkową
jest symetrią
środkową
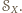 Ponieważ
Ponieważ
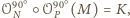 więc
środek
więc
środek
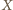 tej symetrii pokrywa się ze środkiem
tej symetrii pokrywa się ze środkiem
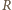 odcinka
odcinka
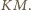 Ponadto z
Ponadto z
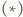 wynika również, że
wynika również, że
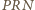 jest
prostokątnym trójkątem równoramiennym. Z zadania 4 wynika, że
jest
prostokątnym trójkątem równoramiennym. Z zadania 4 wynika, że
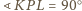 oraz
oraz
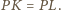 Tak więc
Tak więc
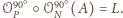 Stąd
Stąd
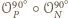 jest symetrią środkową względem środka
jest symetrią środkową względem środka
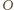 odcinka
odcinka
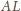 oraz tak jak poprzednio
oraz tak jak poprzednio
 jest prostokątnym
trójkątem równoramiennym. Ostatecznie czworokąt
jest prostokątnym
trójkątem równoramiennym. Ostatecznie czworokąt
 jest
kwadratem.
jest
kwadratem.
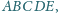 w którym
w którym
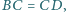
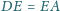 oraz
oraz
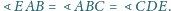 Wykazać, że
w pięciokąt
Wykazać, że
w pięciokąt
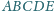 można wpisać okrąg.
można wpisać okrąg.
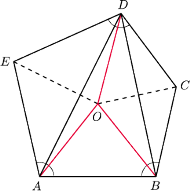
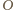 punkt przecięcia dwusiecznych kątów
punkt przecięcia dwusiecznych kątów
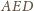 i
i
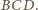
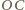 i
i
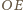 są symetralnymi odpowiednio odcinków
są symetralnymi odpowiednio odcinków
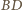 i
i
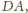 a więc punkt
a więc punkt
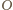 jest środkiem okręgu
opisanego na trójkącie
jest środkiem okręgu
opisanego na trójkącie
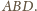 Zatem
Zatem
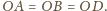 Wobec tego trójkąty
Wobec tego trójkąty
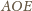 i
i
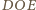 są przystające (cecha
bok-bok-bok), skąd
są przystające (cecha
bok-bok-bok), skąd
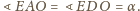 Analogicznie otrzymujemy
Analogicznie otrzymujemy
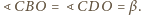 Ponadto
Ponadto
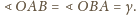 Stąd
korzystając z danych w treści zadania równości kątów, wnioskujemy, że
Stąd
korzystając z danych w treści zadania równości kątów, wnioskujemy, że
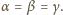 Zależności te z kolei dowodzą, że punkt
Zależności te z kolei dowodzą, że punkt
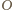 leży na
dwusiecznych kątów
leży na
dwusiecznych kątów
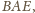
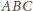 i
i
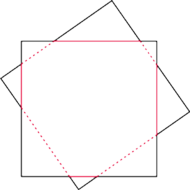
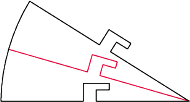
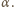 Oznaczając sumę długości
kolorowych odcinków ciągłych przez
Oznaczając sumę długości
kolorowych odcinków ciągłych przez
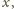 a przerywanych przez
a przerywanych przez
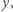 widać, że obwód jednego kwadratu jest równy
widać, że obwód jednego kwadratu jest równy
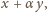 a drugiego
a drugiego
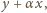 co po przyrównaniu daje
co po przyrównaniu daje
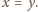
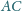 i
i
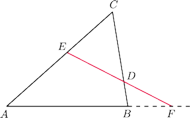
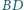 czworokąta wypukłego
czworokąta wypukłego
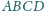 przecinają
się w punkcie
przecinają
się w punkcie
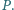 Punkt
Punkt
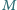 jest środkiem boku
jest środkiem boku
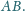 Prosta
Prosta
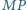 przecina bok
przecina bok
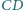 w punkcie
w punkcie
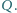 Udowodnij, że
stosunek pól trójkątów
Udowodnij, że
stosunek pól trójkątów
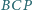 i
i
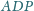 jest równy stosunkowi
długości odcinków
jest równy stosunkowi
długości odcinków
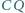 i
i
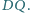
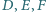 należą odpowiednio do boków
należą odpowiednio do boków
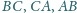 trójkąta ostrokątnego
trójkąta ostrokątnego
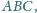 przy czym
przy czym
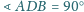 oraz
oraz
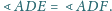 Wykaż, że proste
Wykaż, że proste
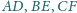 przecinają się
w jednym punkcie.
przecinają się
w jednym punkcie.
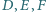 są punktami styczności okręgów dopisanych do trójkąta
są punktami styczności okręgów dopisanych do trójkąta
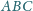 odpowiednio do boków
odpowiednio do boków
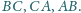 Wykaż, że
proste
Wykaż, że
proste
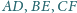 przecinają się w jednym punkcie (tzw. punkcie
Nagela).
przecinają się w jednym punkcie (tzw. punkcie
Nagela).
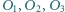 o środkach
odpowiednio
o środkach
odpowiednio
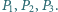 Te dwie styczne do obu okręgów
Te dwie styczne do obu okręgów
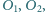 które rozdzielają te okręgi, przecinają się w punkcie
które rozdzielają te okręgi, przecinają się w punkcie
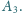 Punkty
Punkty
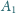 i
i
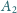 zdefiniowane są analogicznie. Wykaż, że proste
zdefiniowane są analogicznie. Wykaż, że proste
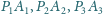 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
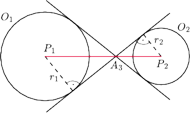
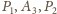 są współliniowe i z twierdzenia Talesa
są współliniowe i z twierdzenia Talesa
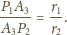
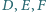 należą odpowiednio do boków
należą odpowiednio do boków
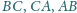 trójkąta
trójkąta
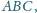 proste
proste
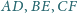 przecinają się w jednym
punkcie. Proste
przecinają się w jednym
punkcie. Proste
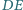 i
i
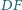 przecinają prostą równoległą do
przecinają prostą równoległą do
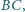 przechodzącą przez punkt
przechodzącą przez punkt
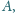 odpowiednio w punktach
odpowiednio w punktach
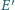 i
i
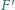 . Udowodnij, że punkt
. Udowodnij, że punkt
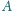 jest środkiem odcinka
jest środkiem odcinka
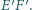
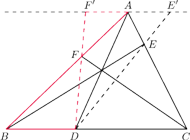
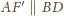 , to
, to
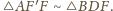 Stąd
Stąd

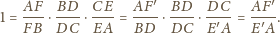
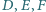 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt
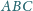 odpowiednio do boków
odpowiednio do boków
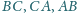 . Wykaż, że
proste
. Wykaż, że
proste
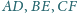 przecinają się w jednym punkcie (tzw. punkcie
Gergonne’a).
przecinają się w jednym punkcie (tzw. punkcie
Gergonne’a).
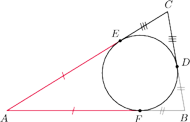
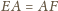 ,
,
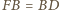 ,
,
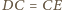 . Stąd
. Stąd
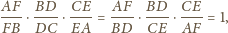
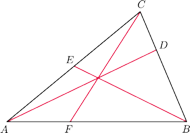
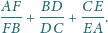
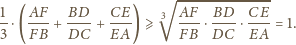
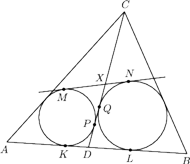
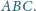 Rozważamy punkt
Rozważamy punkt
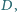 zmieniający swoje
położenie na boku
zmieniający swoje
położenie na boku
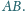 Prosta styczna do okręgów wpisanych
w trójkąty
Prosta styczna do okręgów wpisanych
w trójkąty
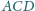 i
i
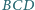 , rozłączna z odcinkiem
, rozłączna z odcinkiem
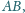 przecina odcinek
przecina odcinek
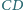 w punkcie
w punkcie
 Udowodnić, że wszystkie
uzyskane w ten sposób punkty
Udowodnić, że wszystkie
uzyskane w ten sposób punkty
 leżą na pewnym okręgu.
leżą na pewnym okręgu.
 i
i
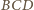 są
styczne do boku
są
styczne do boku
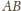 odpowiednio w punktach
odpowiednio w punktach
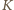 i
i
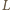 ;
do prostej przechodzącej przez
;
do prostej przechodzącej przez
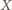 – odpowiednio w punktach
– odpowiednio w punktach
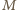 i
i
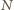 ; zaś do odcinka
; zaś do odcinka
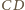 – odpowiednio w punktach
– odpowiednio w punktach
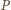 i
i
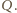
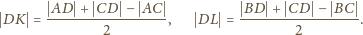
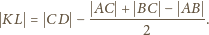
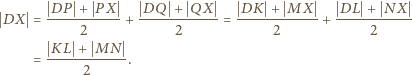
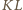 i
i
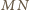 są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
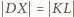 .
.
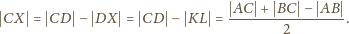
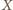 leży na okręgu o środku
leży na okręgu o środku
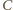 i promieniu
zależnym jedynie od trójkąta
i promieniu
zależnym jedynie od trójkąta
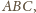 a nie od położenia punktu
a nie od położenia punktu
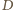 na boku
na boku
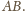
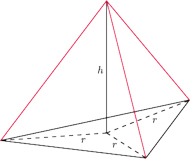
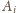 oraz
długość krawędzi wychodzących z wierzchołka
oraz
długość krawędzi wychodzących z wierzchołka
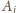 przez
przez
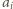 ,
gdzie
,
gdzie
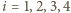 . Wtedy krawędź
. Wtedy krawędź
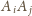 , gdzie
, gdzie
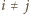 ,
wychodzi z wierzchołka
,
wychodzi z wierzchołka
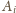 oraz z wierzchołka
oraz z wierzchołka
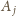 . Oznacza to,
że
. Oznacza to,
że
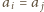 , a więc czworościan jest foremny.
, a więc czworościan jest foremny.
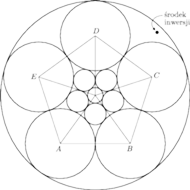
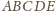 i rysujemy pięć
okręgów o środkach w jego wierzchołkach, o jednakowym promieniu
i rysujemy pięć
okręgów o środkach w jego wierzchołkach, o jednakowym promieniu
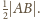 Niech
Niech
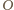 będzie środkiem pięciokąta. W trójkącie
będzie środkiem pięciokąta. W trójkącie
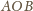 umieszczamy okrąg styczny do odcinków
umieszczamy okrąg styczny do odcinków
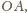
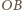 oraz do
narysowanych już okręgów o środkach
oraz do
narysowanych już okręgów o środkach
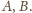 Podobne okręgi umieszczamy
w trójkątach
Podobne okręgi umieszczamy
w trójkątach
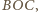
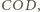
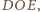
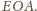 Wreszcie
rysujemy dwa okręgi o środku
Wreszcie
rysujemy dwa okręgi o środku
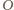 : mały, styczny zewnętrznie do pięciu
okręgów, narysowanych przed chwilą – oraz duży, styczny do pięciu okręgów,
narysowanych na początku i zawierający je wewnątrz.
: mały, styczny zewnętrznie do pięciu
okręgów, narysowanych przed chwilą – oraz duży, styczny do pięciu okręgów,
narysowanych na początku i zawierający je wewnątrz.
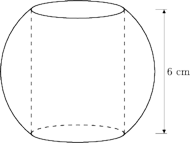

 (licząc
od wierzchołków) leżą na jednej sferze.
(licząc
od wierzchołków) leżą na jednej sferze.
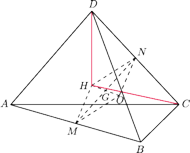
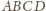 niech
niech
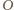 będzie
środkiem sfery opisanej, a
będzie
środkiem sfery opisanej, a
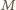 i
i
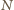 – środkami krawędzi
– środkami krawędzi
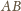 i
i
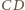 . Przez
. Przez
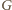 oznaczmy środek odcinka
oznaczmy środek odcinka
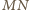 ,
czyli środek ciężkości czworościanu
,
czyli środek ciężkości czworościanu
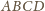 . Niech
. Niech
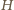 będzie
punktem symetrycznym do
będzie
punktem symetrycznym do
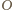 względem
względem
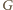 (rysunek). Punkty
(rysunek). Punkty
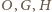 leżą wtedy na jednej prostej, a
leżą wtedy na jednej prostej, a
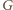 jest środkiem
odcinka
jest środkiem
odcinka
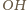 . Wobec tego chcemy wykazać, że
. Wobec tego chcemy wykazać, że
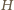 jest
ortocentrum czworościanu
jest
ortocentrum czworościanu
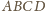 .
.
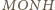 jest równoległobokiem.
W szczególności proste
jest równoległobokiem.
W szczególności proste
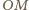 i
i
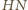 są równoległe. Z definicji
punktów
są równoległe. Z definicji
punktów
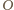 i
i
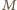 wynika, że odcinki
wynika, że odcinki
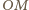 i
i
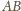 są
prostopadłe, więc również
są
prostopadłe, więc również
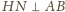 . Stąd i z prostopadłości
prostych
. Stąd i z prostopadłości
prostych
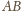 i
i
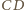 (
(
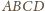 jest ortocentryczny!)
wynika, że płaszczyzna
jest ortocentryczny!)
wynika, że płaszczyzna
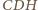 jest prostopadła do prostej
jest prostopadła do prostej
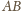 .
W takim razie prosta
.
W takim razie prosta
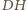 jest prostopadła do prostej
jest prostopadła do prostej
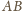 .
Analogicznie dowodzimy, że
.
Analogicznie dowodzimy, że
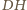 jest prostopadła również do
prostej
jest prostopadła również do
prostej
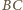 .
.
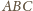 , czyli
stanowi wysokość czworościanu
, czyli
stanowi wysokość czworościanu
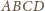 . Podobnie dowodzimy, że
proste
. Podobnie dowodzimy, że
proste
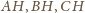 są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
są wysokościami rozpatrywanego czworościanu, co
kończy dowód.
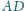 czworościanu
czworościanu
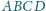 jest prostopadła do
płaszczyzny
jest prostopadła do
płaszczyzny
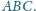 Wykazać, że rzut prostokątny ortocentrum
trójkąta
Wykazać, że rzut prostokątny ortocentrum
trójkąta
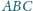 na płaszczyznę
na płaszczyznę
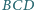 jest ortocentrum trójkąta
jest ortocentrum trójkąta