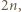Niech liczba boków wielokąta będzie równa a jego wierzchołkami będą kolejno 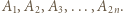Dla 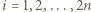niech

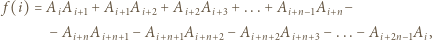
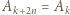gdzie dla 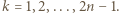Innymi słowy, 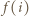jest różnicą długości części, na które dzielą obwód wielokąta punkty 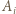oraz 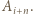Ponieważ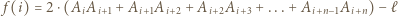

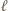(gdzie jest obwodem danego wielokąta), to 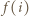jest liczbą parzystą. Ponadto mamy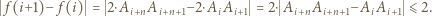

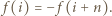Zachodzi także równość Stąd wynika, że ciąg liczb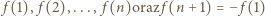

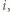składa się z liczb parzystych, a jego kolejne wyrazy różnią się nie więcej niż o 2. Zatem istnieje takie że 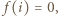czyli punkty 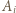oraz 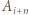dzielą obwód danego wielokąta na dwie części o jednakowej długości.