Zadania z matematyki - IV 2020»Zadanie 1635
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - IV 2020
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Prostokąt nazwiemy parzystym, jeśli każdy z jego wymiarów jest parzystą liczbą całkowitą. Kwadrat 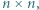 gdzie
gdzie 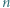 jest liczbą nieparzystą, podzielono na części, z których każda jest parzystym prostokątem lub kwadratem
jest liczbą nieparzystą, podzielono na części, z których każda jest parzystym prostokątem lub kwadratem 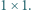 Znaleźć najmniejszą możliwą liczbę kwadratów
Znaleźć najmniejszą możliwą liczbę kwadratów 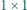 uzyskanych w takim podziale.
uzyskanych w takim podziale.

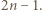
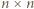 na
na 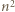 kwadratów jednostkowych, zwanych dalej polami, i wyróżnijmy pola znajdujące się na przecięciach wierszy i kolumn o parzystych numerach. Takich pól jest
kwadratów jednostkowych, zwanych dalej polami, i wyróżnijmy pola znajdujące się na przecięciach wierszy i kolumn o parzystych numerach. Takich pól jest 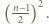
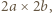 a więc o polu
a więc o polu 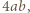 zawiera dokładnie
zawiera dokładnie 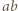 wyróżnionych pól. Wobec tego łączne pole części podziału będących parzystymi prostokątami jest równe co najwyżej
wyróżnionych pól. Wobec tego łączne pole części podziału będących parzystymi prostokątami jest równe co najwyżej 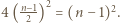 Łączne pole kwadratów jednostkowych jest zatem równe co najmniej
Łączne pole kwadratów jednostkowych jest zatem równe co najmniej 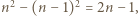 skąd wniosek, że jest co najmniej tyle takich kwadratów.
skąd wniosek, że jest co najmniej tyle takich kwadratów.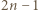 kwadratów jednostkowych, jest możliwy - wystarczy wyciąć kwadrat o boku
kwadratów jednostkowych, jest możliwy - wystarczy wyciąć kwadrat o boku 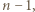 a pozostałą część podzielić na kwadraty jednostkowe.
a pozostałą część podzielić na kwadraty jednostkowe.