Równoległobok»Zadanie 7
o zadaniu...
- Zadanie pochodzi z artykułu Równoległobok
- Publikacja w Delcie: czerwiec 2020
- Publikacja elektroniczna: 31 maja 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (346 KB)
Niech 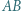 będzie krótszym łukiem okręgu
będzie krótszym łukiem okręgu 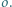 Na łuku
Na łuku 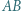 wybieramy punkt
wybieramy punkt 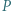 różny od
różny od 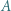 i
i 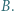 Punkt
Punkt 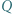 leży na prostej
leży na prostej 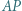 i spełnia równość
i spełnia równość 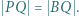 Punkt
Punkt 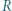 leży na prostej
leży na prostej 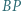 i spełnia warunek
i spełnia warunek 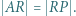 Wreszcie punkt
Wreszcie punkt 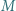 jest środkiem odcinka
jest środkiem odcinka 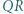 i przez
i przez 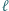 oznaczamy prostą
oznaczamy prostą 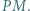 Dowieść, że wszystkie otrzymane w ten sposób proste
Dowieść, że wszystkie otrzymane w ten sposób proste 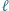 (dla różnych punktów
(dla różnych punktów 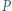 ) mają punkt wspólny.
) mają punkt wspólny.

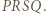 Jest oczywiste, że prosta
Jest oczywiste, że prosta 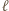 przechodzi przez punkt
przechodzi przez punkt 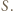 Okrąg opisany na trójkącie
Okrąg opisany na trójkącie 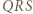 przechodzi przez punkty
przechodzi przez punkty 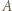 i
i 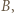 ponadto
ponadto 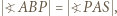 więc prosta
więc prosta 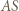 jest styczna do okręgu
jest styczna do okręgu 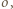 analogicznie prosta
analogicznie prosta 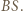 Położenie punktu
Położenie punktu 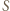 nie zależy zatem od wyboru punktu
nie zależy zatem od wyboru punktu