Potęga punktu względem okręgu»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Potęga punktu względem okręgu
- Publikacja w Delcie: listopad 2019
- Publikacja elektroniczna: 31 października 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (417 KB)
Odrobina klasyki:
- (a)
- W kąt o wierzchołku
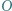 wpisano dwa okręgi:
wpisano dwa okręgi: 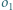 styczny do ramion kąta w punktach
styczny do ramion kąta w punktach 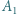 i
i 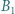 oraz
oraz 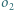 - w punktach
- w punktach 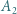 i
i 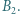 Wykazać, że okręgi te wyznaczają cięciwy jednakowej długości na ich wspólnej siecznej
Wykazać, że okręgi te wyznaczają cięciwy jednakowej długości na ich wspólnej siecznej 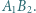
- (b)
- Na każdej wspólnej stycznej dwóch rozłącznych zewnętrznie okręgów zaznaczono odcinek łączący punkty styczności. Dowieść, że środki wszystkich czterech zaznaczonych odcinków leżą na jednej prostej.
- (c)
- Okręgi
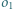 i
i 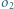 przecinają się w punktach
przecinają się w punktach 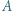 i
i 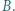 Z punktu
Z punktu 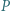 leżącego na prostej
leżącego na prostej 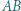 poprowadzono styczną do
poprowadzono styczną do 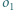 w punkcie
w punkcie 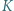 i do
i do 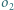 w punkcie
w punkcie 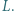 Udowodnić, że trójkąt
Udowodnić, że trójkąt 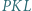 jest równoramienny.
jest równoramienny.
