Koła, półkola i pola»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Koła, półkola i pola
- Publikacja w Delcie: luty 2018
- Publikacja elektroniczna: 1 lutego 2018
- Artykuł źródłowy w wersji do druku [application/pdf]: (111 KB)
Wewnątrz trójkąta 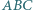 leży punkt
leży punkt 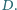 Proste
Proste 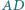 i
i 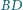 przecinają boki
przecinają boki  i
i 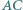 odpowiednio w punktach
odpowiednio w punktach 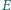 i
i 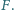 Udowodnić, że jeśli
Udowodnić, że jeśli 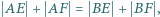 to
to 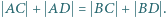
Dany jest okrąg 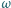 o średnicy
o średnicy 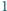 oraz łamana
oraz łamana  o końcach należących do tego okręgu, której długość jest mniejsza od
o końcach należących do tego okręgu, której długość jest mniejsza od  Udowodnić, że istnieje średnica okręgu
Udowodnić, że istnieje średnica okręgu 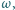 która jest rozłączna z
która jest rozłączna z 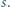
Trójkąt równoboczny o boku długości 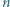 został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 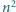 trójkątów o boku 1 (trójkątów jednostkowych). Wierzchołkom powstałej siatki zostały przyporządkowane różne liczby rzeczywiste (
trójkątów o boku 1 (trójkątów jednostkowych). Wierzchołkom powstałej siatki zostały przyporządkowane różne liczby rzeczywiste ( 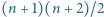 różnych liczb). Trójkąt jednostkowy nazwiemy zorientowanym dodatnio, jeśli - idąc wzdłuż jego brzegu, w kierunku wzrastania liczb przy wierzchołkach (tj. startując od najmniejszej i idąc przez średnią do największej) - mamy jego wnętrze po lewej stronie. Dla ustalonej liczby naturalnej
różnych liczb). Trójkąt jednostkowy nazwiemy zorientowanym dodatnio, jeśli - idąc wzdłuż jego brzegu, w kierunku wzrastania liczb przy wierzchołkach (tj. startując od najmniejszej i idąc przez średnią do największej) - mamy jego wnętrze po lewej stronie. Dla ustalonej liczby naturalnej  wyznaczyć najmniejszą i największą możliwą wartość liczby trójkątów jednostkowych zorientowanych dodatnio.
wyznaczyć najmniejszą i największą możliwą wartość liczby trójkątów jednostkowych zorientowanych dodatnio.
Trójkąt 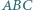 jest opisany na okręgu o środku
jest opisany na okręgu o środku 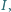 stycznym do boków
stycznym do boków 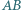 i
i 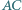 w punktach
w punktach 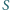 i
i 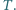 Na boku
Na boku  leży taki punkt
leży taki punkt 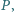 że
że 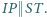 Proste
Proste 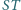 i
i 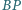 przecinają się w punkcie
przecinają się w punkcie 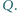 Dowieść, że
Dowieść, że 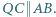
Mamy dwa ziemniaki. Wykaż, że istnieje taka krzywa zamknięta w przestrzeni trójwymiarowej, którą da się narysować na powierzchni każdego z tych ziemniaków.
Czy istnieje w przestrzeni taka łamana zwyczajna zamknięta, której żaden z rzutów na płaszczyzny w ustalonych trzech wzajemnie prostopadłych kierunkach nie zawiera łamanej zamkniętej?
Pewnego poranka o godzinie 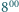 turysta wyruszył z domu u podnóża góry i o
turysta wyruszył z domu u podnóża góry i o 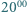 dotarł do schroniska na szczycie. O
dotarł do schroniska na szczycie. O 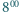 następnego dnia wyruszył ze szczytu tą samą trasą i o
następnego dnia wyruszył ze szczytu tą samą trasą i o 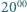 wrócił do domu. Udowodnij, że istnieje taki punkt, w którym turysta był w oba dni dokładnie o tej samej godzinie.
wrócił do domu. Udowodnij, że istnieje taki punkt, w którym turysta był w oba dni dokładnie o tej samej godzinie.
W przestrzeni dana jest łamana zwyczajna zamknięta złożona z sześciu równej długości odcinków, przy czym odcinki pierwszy i czwarty, drugi i piąty oraz trzeci i szósty są parami równoległe. Ponadto każde dwie proste zawierające kolejne odcinki łamanej tworzą kąty płaskie równe  Czy łamana ta musi być sześciokątem foremnym?
Czy łamana ta musi być sześciokątem foremnym?
Robaczek wgryzł się w idealnie kuliste jabłko o średnicy 1, wydrążył w nim cieniutki tunelik o długości 0,9 i o sobie tylko znanym kształcie i wyszedł na powierzchnię w innym punkcie. Wykaż, że można to jabłko tak przeciąć na pół, by w jednej z połówek nie było śladów bytności robaczka.
Punkt 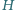 jest ortocentrum trójkąta ostrokątnego
jest ortocentrum trójkąta ostrokątnego 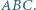 Wykaż, że okręgi opisane na trójkątach
Wykaż, że okręgi opisane na trójkątach  i
i 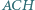 są przystające.
są przystające.
Trójkąt prostokątny 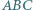 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 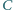 obrócono wokół prostej
obrócono wokół prostej  otrzymując dwa stożki obrotowe o wspólnej podstawie, której brzegiem jest okrąg
otrzymując dwa stożki obrotowe o wspólnej podstawie, której brzegiem jest okrąg  Sfera
Sfera 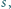 do której należy punkt
do której należy punkt 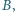 jest styczna do sfery
jest styczna do sfery 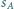 o środku
o środku 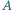 i promieniu
i promieniu 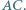 Sfery
Sfery 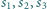 są styczne do sfery
są styczne do sfery  oraz do sfery
oraz do sfery  w pewnych punktach należących do okręgu
w pewnych punktach należących do okręgu 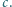 Udowodnić, że sfery
Udowodnić, że sfery 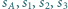 mają wspólną płaszczyznę styczną.
mają wspólną płaszczyznę styczną.
Na obwodzie trójkąta 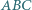 leżą cztery różne punkty
leżą cztery różne punkty  : punkty
: punkty 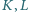 na boku
na boku 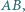 punkty
punkty 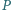 i
i 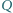 odpowiednio na bokach
odpowiednio na bokach 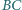 i
i 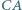 ; przy tym odcinki
; przy tym odcinki 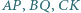 i
i 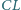 mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.
mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.
Rozstrzygnij, czy istnieje takich 100 punktów na płaszczyźnie, z których każde trzy są wierzchołkami trójkąta rozwartokątnego.
Podziel kwadrat na 8 trójkątów ostrokątnych.
Zadanie 4 jest modyfikacją zadania z XXV Olimpiady Matematycznej. Więcej o nim m.in. w Delcie 5/1986.
W czworościanie 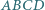 krawędź
krawędź  jest prostopadła do krawędzi
jest prostopadła do krawędzi 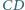 i
i 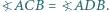 Rozstrzygnij, czy oznacza to, że płaszczyzna wyznaczona przez krawędź
Rozstrzygnij, czy oznacza to, że płaszczyzna wyznaczona przez krawędź  i środek krawędzi
i środek krawędzi 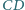 jest prostopadła do krawędzi
jest prostopadła do krawędzi 
Skonstruuj trójkąt  mając dane punkty
mając dane punkty 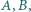 kąt przy wierzchołku
kąt przy wierzchołku 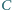 oraz długość środkowej
oraz długość środkowej 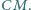 Ile rozwiązań może mieć to zadanie?
Ile rozwiązań może mieć to zadanie?
Punkty  i
i  należą do wnętrza kąta ostrego
należą do wnętrza kąta ostrego 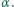 Skonstruuj taki trójkąt równoramienny, aby punkty
Skonstruuj taki trójkąt równoramienny, aby punkty 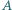 i
i 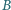 należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta
należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta 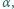 a wierzchołek należał do drugiego z ramion.
a wierzchołek należał do drugiego z ramion.
Udowodnij stwierdzenia z drugiego akapitu niniejszego artykułu.
Punkt 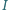 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt  Prosta
Prosta 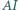 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie  w punktach
w punktach  i
i 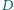 ; prosta
; prosta 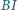 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 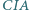 w punktach
w punktach  i
i 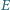 ; prosta
; prosta  przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie  w punktach
w punktach 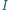 i
i 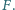 Wyznaczyć największą możliwą wartość iloczynu
Wyznaczyć największą możliwą wartość iloczynu 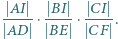
Niech  będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać
będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać  -kąta foremnego.
-kąta foremnego.
Znaleźć największą liczbę naturalną 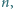 dla której
dla której  jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
W dwa trójkąty, o bokach odpowiednio 17, 25, 26 i 17, 25, 28, wpisujemy koła. Które z wpisanych kół ma większy promień?
Dwa okręgi, styczne zewnętrznie w punkcie  są styczne do prostej
są styczne do prostej 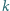 w punktach
w punktach 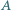 i
i 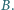 Wykaż, że trójkąt
Wykaż, że trójkąt 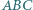 jest prostokątny.
jest prostokątny.
Wykaż, że jeżeli przekątne pewnego trapezu są prostopadłe, to suma długości podstaw tego trapezu jest nie większa od sumy długości jego ramion.