Nigdy Cię nie zobaczę?
- Hop, hop, jest tam kto? - krzyczy 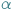 otoczona tłumem.
otoczona tłumem.
- Hop, hop, spójrz tutaj. - odpowiada 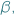 który co prawda słyszy
który co prawda słyszy 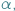 ale zupełnie jej nie widzi.
ale zupełnie jej nie widzi.
- Jakie "tutaj"? Przecież dookoła nie ma żywej duszy. - 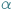 otoczona tłumem po raz kolejny usiłuje dostrzec
otoczona tłumem po raz kolejny usiłuje dostrzec 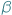 pośród otaczającej pustki.
pośród otaczającej pustki.



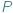 będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez
będzie wielościanem wypukłym o trójkątnych ścianach. Oznaczmy przez 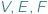 odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki
odpowiednio liczbę jego wierzchołków, krawędzi i ścian. Jakie trójki 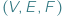 liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości:
liczb naturalnych możemy w ten sposób uzyskać? Bez trudu możemy wypisać dwie równości: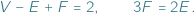

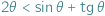 dla dowolnego kąta ostrego
dla dowolnego kąta ostrego 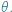 Podaną nierówność można łatwo udowodnić, używając rachunku różniczkowego. Można jednak zadać pytanie: czy da się tego uniknąć, czy można ją wykazać krócej, używając przy tym jedynie elementarnej geometrii. Okazuje się, że tak.
Podaną nierówność można łatwo udowodnić, używając rachunku różniczkowego. Można jednak zadać pytanie: czy da się tego uniknąć, czy można ją wykazać krócej, używając przy tym jedynie elementarnej geometrii. Okazuje się, że tak.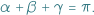
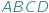 i
i 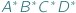 takie, że każdemu bokowi jednego odpowiada pewien równoległy doń bok drugiego, a każdej przekątnej - równoległa przekątna. Na pierwszy rzut oka wydawać by się mogło, że takie czworokąty muszą być podobne, jest jednak druga możliwość - wówczas czworokąty te są bliźniacze...
takie, że każdemu bokowi jednego odpowiada pewien równoległy doń bok drugiego, a każdej przekątnej - równoległa przekątna. Na pierwszy rzut oka wydawać by się mogło, że takie czworokąty muszą być podobne, jest jednak druga możliwość - wówczas czworokąty te są bliźniacze...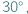 to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
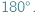 Jednakże wszystkie takie sprawdzenia tego i innych twierdzeń geometrii euklidesowej możemy wykonać jedynie w pewnym otoczeniu Ziemi, którego promień jest wyznaczony zasięgiem naszych teleskopów...
Jednakże wszystkie takie sprawdzenia tego i innych twierdzeń geometrii euklidesowej możemy wykonać jedynie w pewnym otoczeniu Ziemi, którego promień jest wyznaczony zasięgiem naszych teleskopów...
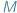 ) przypiszemy odległość, zwaną także metryką (oznaczamy ją przez
) przypiszemy odległość, zwaną także metryką (oznaczamy ją przez 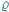 ), to powstanie przestrzeń metryczna
), to powstanie przestrzeń metryczna 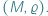


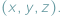 Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych
Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych 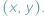 Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej
Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej 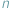 -wymiarową, używamy zestawu
-wymiarową, używamy zestawu 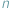 liczb
liczb 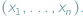


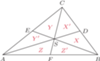
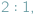 licząc od wierzchołka trójkąta (rys. obok).
licząc od wierzchołka trójkąta (rys. obok).