Zadanie ZM-1608
o zadaniu...
- Publikacja w Delcie: lipiec 2019
- Publikacja elektroniczna: 1 lipca 2019
Dana jest triangulacja pewnego  -kąta, przy czym
-kąta, przy czym 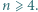 Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego
Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego  -kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego
-kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego  -kąta. Wykazać, że liczba czarnych trójkątów jest o
-kąta. Wykazać, że liczba czarnych trójkątów jest o 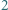 większa od liczby białych trójkątów.
większa od liczby białych trójkątów.

 -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 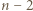 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).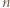 -kąta i oznaczmy przez
-kąta i oznaczmy przez 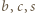 odpowiednio liczby białych, czarnych i szarych trójkątów.
odpowiednio liczby białych, czarnych i szarych trójkątów.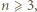 to nie istnieje trójkąt, którego wszystkie boki są także bokami danego
to nie istnieje trójkąt, którego wszystkie boki są także bokami danego  -kąta, więc każdy z
-kąta, więc każdy z 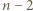 trójkątów został pomalowany dokładnie jednym kolorem, czyli
trójkątów został pomalowany dokładnie jednym kolorem, czyli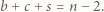
 -kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd
-kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd