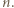Nazwijmy trójkąt wyznaczony przez trzy spośród wierzchołków danego 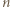 -kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.
-kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.
Przypuśćmy, że istnieją dwa różne trójkąty czadowe o tych samych kolorach boków. Z konstrukcji kolorowania odcinków wynika więc, że mają one parami równoległe boki, a więc są jednokładne. Skoro są wpisane w ten sam okrąg (opisany na danym 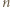 -kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego
-kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego 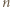 -kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że
-kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że 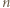 jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.
jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.
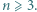 Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 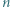 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 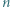 -kąta.
-kąta.
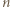 -kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.
-kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.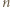 -kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego
-kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego 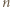 -kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że
-kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że 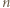 jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.
jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.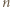 -kąta kolejnymi resztami z dzielenia przez
-kąta kolejnymi resztami z dzielenia przez 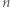 i zauważmy, że odcinki
i zauważmy, że odcinki 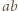 oraz
oraz 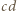 mają ten sam kolor wtedy i tylko wtedy, gdy
mają ten sam kolor wtedy i tylko wtedy, gdy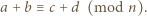
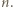
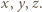 Trójkąt
Trójkąt 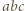 ma boki
ma boki 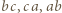 odpowiednio w tych kolorach wtedy i tylko wtedy, gdy
odpowiednio w tych kolorach wtedy i tylko wtedy, gdy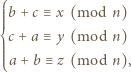
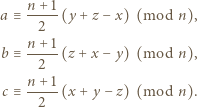
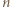 jest liczbą nieparzystą, więc trójka
jest liczbą nieparzystą, więc trójka 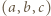 jest wyznaczona jednoznacznie z dokładnością do reszty z dzielenia przez
jest wyznaczona jednoznacznie z dokładnością do reszty z dzielenia przez