Środek ciężkości II»Zadanie 7
o zadaniu...
- Zadanie pochodzi z artykułu Środek ciężkości II
- Publikacja w Delcie: grudzień 2011
- Publikacja elektroniczna: 01-12-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (105 KB)
Punkty
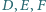 należą odpowiednio do boków
należą odpowiednio do boków
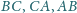 trójkąta
trójkąta
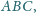 proste
proste
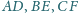 przecinają się w punkcie
przecinają się w punkcie
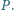 Wykaż,
że
Wykaż,
że
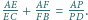
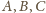 takie masy
takie masy
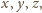 by
by
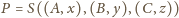 (czy zawsze się da?). Wtedy
(czy zawsze się da?). Wtedy
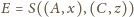 (bo
(bo
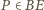 ), zatem
), zatem
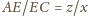 i analogicznie
i analogicznie
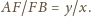
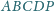 jest równoległobok
jest równoległobok
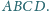 Punkty
Punkty
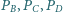 na krawędziach
na krawędziach
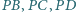 spełniają warunki:
spełniają warunki:
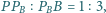
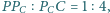
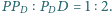 Płaszczyzna
Płaszczyzna
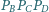 przecina krawędź
przecina krawędź
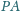 w punkcie
w punkcie
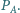 Wyznacz
Wyznacz
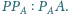
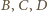 masy odpowiednio
masy odpowiednio
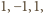 a w punkcie
a w punkcie
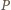 trzy masy:
trzy masy:
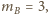
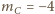 i
i
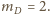 Wtedy
Wtedy
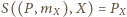 dla
dla
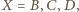 więc środek ciężkości
więc środek ciężkości
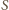 układu
układu
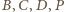 leży na płaszczyźnie
leży na płaszczyźnie
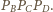 Ponadto
Ponadto
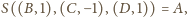 bo
bo
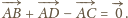 Skoro
Skoro
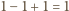 oraz
oraz
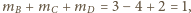 to
to
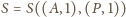 jest środkiem odcinka
jest środkiem odcinka
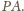 Stąd
i z wcześniejszego
Stąd
i z wcześniejszego
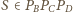 wynika
wynika
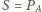 i
i
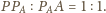
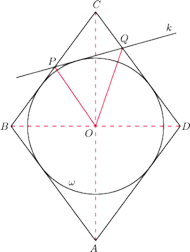
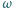 jest wpisany w romb
jest wpisany w romb
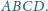 Prosta
Prosta
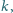 styczna do
okręgu
styczna do
okręgu
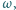 przecina odcinki
przecina odcinki
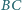 i
i
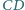 odpowiednio
w punktach
odpowiednio
w punktach
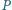 i
i
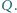 Wykaż, że wartość iloczynu
Wykaż, że wartość iloczynu
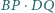 nie zależy od wyboru stycznej
nie zależy od wyboru stycznej
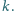
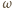 jest wpisany w romb
jest wpisany w romb
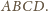 Prosta
Prosta
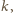 styczna do
okręgu
styczna do
okręgu
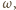 przecina odcinki
przecina odcinki
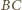 i
i
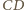 odpowiednio
w punktach
odpowiednio
w punktach
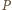 i
i
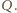 Wykaż, że wartość iloczynu
Wykaż, że wartość iloczynu
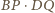 nie zależy od wyboru stycznej
nie zależy od wyboru stycznej
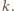
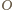 oznacza środek okręgu
oznacza środek okręgu
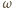 (jest to jednocześnie
punkt przecięcia przekątnych rombu).
(jest to jednocześnie
punkt przecięcia przekątnych rombu).
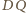 i
i
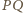 są styczne do okręgu
są styczne do okręgu
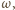 więc
więc
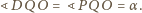
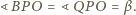
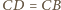 otrzymujemy również, że
otrzymujemy również, że
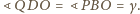 Sumując kąty czworokąta
Sumując kąty czworokąta
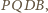 otrzymujemy
otrzymujemy
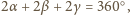 skąd
skąd
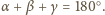 W takim razie
W takim razie
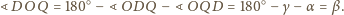
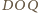 i
i
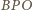 są podobne, skąd mamy
są podobne, skąd mamy
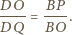
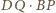 jest stały i wynosi
jest stały i wynosi
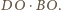
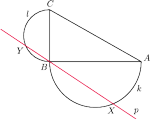
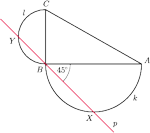
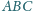 , na przyprostokątnych
, na przyprostokątnych
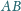 i
i
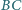 jako na średnicach, zbudowano półokręgi
jako na średnicach, zbudowano półokręgi
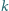 i
i
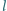 , odpowiednio. Prosta
, odpowiednio. Prosta
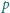 przechodząca przez
punkt
przechodząca przez
punkt
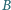 przecina łuki
przecina łuki
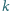 i
i
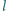 w punktach
w punktach
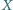 i
i
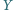 .
Znaleźć położenie tej prostej, dla którego obwód czworokąta
.
Znaleźć położenie tej prostej, dla którego obwód czworokąta
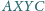 jest maksymalny.
jest maksymalny.
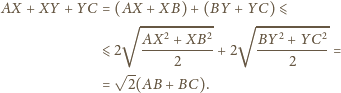
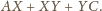 Powyżej zachodzi równość wtedy i tylko wtedy, gdy
Powyżej zachodzi równość wtedy i tylko wtedy, gdy
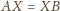 i
i
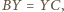 czyli wtedy i tylko wtedy, gdy prosta
czyli wtedy i tylko wtedy, gdy prosta
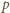 tworzy z półprostą
tworzy z półprostą
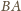 kąt
kąt
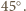
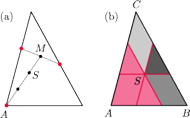
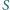 wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
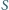 ?
?
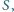 zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
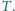 Wykaż, że wszystkie tak wyznaczone
proste
Wykaż, że wszystkie tak wyznaczone
proste
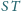 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
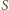 jego wierzchołków, bo obrazem
jego wierzchołków, bo obrazem
 w symetrii względem takiej
osi jest on sam.
w symetrii względem takiej
osi jest on sam.
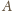 trójkąta. Środek ciężkości pozostałych dwóch
much jest w środku
trójkąta. Środek ciężkości pozostałych dwóch
much jest w środku
 odcinka pomiędzy nimi (
odcinka pomiędzy nimi (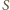 wszystkich much jest na odcinku
wszystkich much jest na odcinku
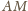 oraz
oraz
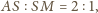 czyli
czyli
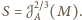 Stąd
Stąd
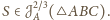
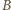 i
i
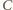 prowadzi do
wniosku, że jedynym możliwym położeniem
prowadzi do
wniosku, że jedynym możliwym położeniem
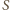 jest środek
ciężkości trójkąta (
jest środek
ciężkości trójkąta (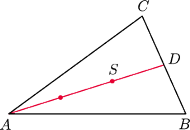
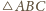 równe masy
równe masy
 Wtedy
Wtedy
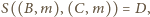 gdzie
gdzie
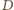 to środek
to środek
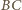 . Środek
ciężkości trójkąta
. Środek
ciężkości trójkąta
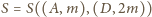 leży na środkowej
leży na środkowej
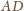 ; analogicznie leży na pozostałych środkowych. Ponadto
; analogicznie leży na pozostałych środkowych. Ponadto
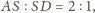 czyli środkowe dzielą się w stosunku
czyli środkowe dzielą się w stosunku
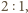 licząc
od wierzchołka.
licząc
od wierzchołka.
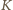 na boku
na boku
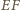 trójkąta
trójkąta
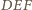 spełnia
spełnia
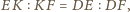 to jest
spodkiem dwusiecznej
to jest
spodkiem dwusiecznej
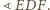
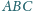 umieszczono masy
odpowiednio
umieszczono masy
odpowiednio
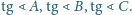 Wykaż, że ich środkiem
ciężkości jest ortocentrum
Wykaż, że ich środkiem
ciężkości jest ortocentrum
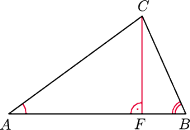
 jest wysokością
jest wysokością
 to
to
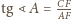 i
i
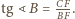 Stąd
Stąd
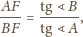
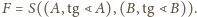 Szukany środek ciężkości
leży więc na
Szukany środek ciężkości
leży więc na
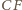 i analogicznie na wysokościach z
i analogicznie na wysokościach z
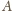 i z
i z
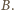
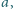
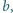
 środkowa
poprowadzona do boku
środkowa
poprowadzona do boku
 ma długość
ma długość
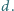 Wykazać, że dla
każdej liczby dodatniej
Wykazać, że dla
każdej liczby dodatniej
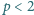 zachodzi nierówność
zachodzi nierówność

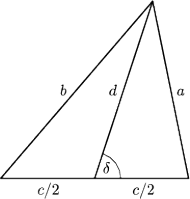
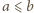 i oznaczmy przez
i oznaczmy przez
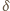 miarę kąta ostrego (lub
prostego), jaki zadana środkowa tworzy z prostą, zawierającą bok
miarę kąta ostrego (lub
prostego), jaki zadana środkowa tworzy z prostą, zawierającą bok
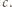 Jest to
kąt wewnętrzny w trójkącie o bokach długości
Jest to
kąt wewnętrzny w trójkącie o bokach długości
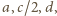 przeciwległy
bokowi
przeciwległy
bokowi
 Ze wzoru kosinusów:
Ze wzoru kosinusów:
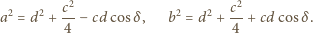
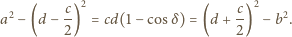
 jest funkcją ściśle wklęsłą (w pewnym przedziale)
i jeśli
jest funkcją ściśle wklęsłą (w pewnym przedziale)
i jeśli
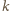 jest stałą dodatnią, to funkcja
jest stałą dodatnią, to funkcja
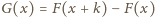 jest
ściśle malejąca. Zastosujmy tę własność do funkcji
jest
ściśle malejąca. Zastosujmy tę własność do funkcji
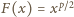 (ściśle
wklęsłej w przedziale
(ściśle
wklęsłej w przedziale
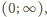 skoro
skoro
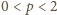 ) oraz do
stałej dodatniej
) oraz do
stałej dodatniej
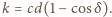 Tworzymy funkcję malejącą
Tworzymy funkcję malejącą
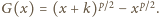
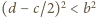 (równoważnie:
(równoważnie:
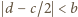 ; jest
to nierówność dla boków jednego z trójkątów, na które środkowa
dzieli trójkąt wyjściowy). Zatem
; jest
to nierówność dla boków jednego z trójkątów, na które środkowa
dzieli trójkąt wyjściowy). Zatem
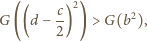
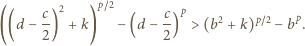
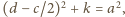
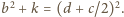 Otrzymujemy
nierówność
Otrzymujemy
nierówność
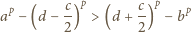
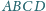 i
i
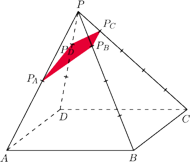
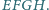 Płaszczyzna
przecina jego krawędzie boczne
Płaszczyzna
przecina jego krawędzie boczne
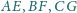 i
i
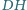 odpowiednio
w punktach
odpowiednio
w punktach
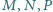 i
i
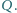 Wykaż, że
Wykaż, że

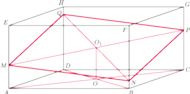
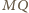 i
i
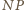 zawierają się w jednej płaszczyźnie
i jednocześnie zawierają się w płaszczyznach równoległych, więc są to odcinki
równoległe. Analogicznie równoległe są odcinki
zawierają się w jednej płaszczyźnie
i jednocześnie zawierają się w płaszczyznach równoległych, więc są to odcinki
równoległe. Analogicznie równoległe są odcinki
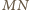 i
i
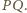 Stąd
czworokąt
Stąd
czworokąt
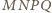 jest równoległobokiem.
jest równoległobokiem.
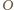 będzie punktem przecięcia przekątnych
będzie punktem przecięcia przekątnych
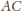 i
i
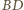 podstawy
podstawy
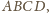 a
a
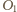 – punktem
przecięcia przekątnych
– punktem
przecięcia przekątnych
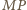 i
i
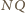 równoległoboku
równoległoboku
 Zauważmy, że odcinek
Zauważmy, że odcinek
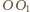 jest odcinkiem
łączącym środki nierównoległych boków trapezów
jest odcinkiem
łączącym środki nierównoległych boków trapezów
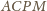 i
i
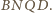 Jest on równoległy do boków równoległych tych trapezów
oraz
Jest on równoległy do boków równoległych tych trapezów
oraz
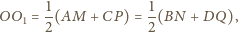
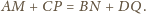
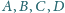 , że
, że
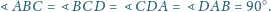
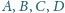 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
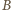 i
i
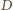 należą do sfery
należą do sfery
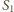 o średnicy
o średnicy
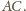 Podobnie, punkty
Podobnie, punkty
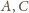 należą do sfery
należą do sfery
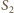 o średnicy
o średnicy
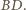 Ale sfera jest
jednoznacznie wyznaczona przez cztery niewspółpłaszczyznowe punkty, więc
Ale sfera jest
jednoznacznie wyznaczona przez cztery niewspółpłaszczyznowe punkty, więc
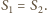 Dwie średnice ustalonej sfery leżą w jednej płaszczyźnie, więc
w szczególności odcinki
Dwie średnice ustalonej sfery leżą w jednej płaszczyźnie, więc
w szczególności odcinki
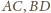 leżą w jednej płaszczyźnie, co
daje tezę.
leżą w jednej płaszczyźnie, co
daje tezę.
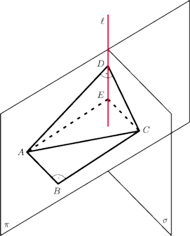
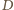 ? Wobec
? Wobec
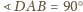 leży on na
płaszczyźnie
leży on na
płaszczyźnie
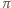 prostopadłej do
prostopadłej do
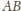 i przechodzącej przez
i przechodzącej przez
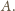 Podobnie wnioskujemy, że punkt
Podobnie wnioskujemy, że punkt
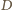 leży na płaszczyźnie
leży na płaszczyźnie
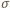 prostopadłej do prostej
prostopadłej do prostej
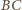 i przechodzącej przez
i przechodzącej przez
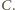 Punkt
Punkt
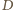 leży więc na prostej
leży więc na prostej
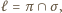 która
przechodzi przez punkt
która
przechodzi przez punkt
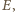 uzupełniający trójkąt
uzupełniający trójkąt
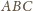 do
prostokąta
do
prostokąta
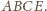
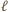 jest rzutem prostokątnym prostej
jest rzutem prostokątnym prostej
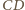 na płaszczyznę
na płaszczyznę
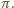 Ponieważ
Ponieważ
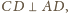 to z twierdzenia o trzech prostopadłych
to z twierdzenia o trzech prostopadłych
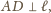 więc
więc
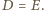 Punkty
Punkty
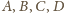 leżą więc na jednej
płaszczyźnie.
leżą więc na jednej
płaszczyźnie.
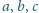 są długościami boków trójkąta, to
zachodzi nierówność
są długościami boków trójkąta, to
zachodzi nierówność
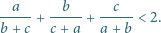
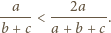

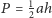
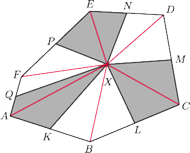
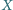 leży wewnątrz sześciokąta wypukłego
leży wewnątrz sześciokąta wypukłego
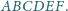 Punkty
Punkty
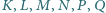 są odpowiednio
środkami boków
są odpowiednio
środkami boków
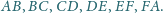 Wykaż, że
Wykaż, że
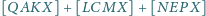 nie zależy od wyboru punktu
nie zależy od wyboru punktu
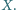
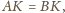 to
to
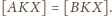 Podobnie
Podobnie
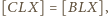
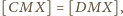
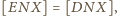
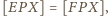
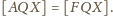 Dodając
stronami, uzyskujemy
Dodając
stronami, uzyskujemy
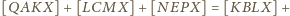
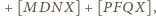 czyli
czyli
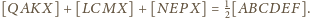
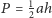
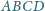 o polu 1. Punkt
o polu 1. Punkt
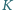 jest
symetryczny do punktu
jest
symetryczny do punktu
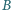 względem punktu
względem punktu
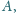 punkt
punkt
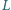 jest
symetryczny do punktu
jest
symetryczny do punktu
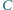 względem punktu
względem punktu
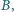 punkt
punkt
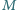 jest symetryczny do punktu
jest symetryczny do punktu
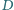 względem punktu
względem punktu
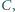 punkt
punkt
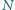 jest symetryczny do punktu
jest symetryczny do punktu
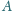 względem
punktu
względem
punktu
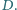 Oblicz
Oblicz
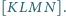
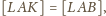 bo trójkąty te mają równe
podstawy
bo trójkąty te mają równe
podstawy
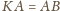 i wspólną wysokość z
i wspólną wysokość z
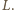 Ponadto
Ponadto
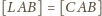 (ponieważ
(ponieważ
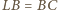 ). Analogicznie
). Analogicznie
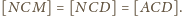 Stąd
Stąd
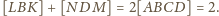 Podobnie
Podobnie
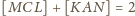 i ostatecznie
i ostatecznie
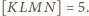
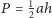
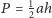
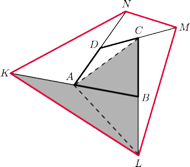
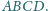 Punkty
Punkty
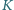 i
i
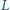 należą
do boku
należą
do boku
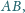 przy czym
przy czym
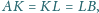 a punkty
a punkty
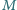 i
i
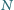 należą do boku
należą do boku
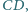 przy czym
przy czym
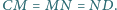 Wykaż,
że
Wykaż,
że
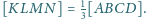
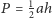
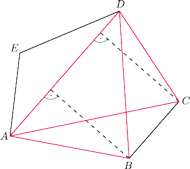
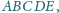 w którym pola trójkątów
w którym pola trójkątów
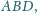
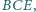
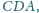
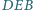 i
i
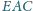 są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Udowodnij, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
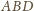 i
i
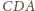 mają wspólną podstawę
mają wspólną podstawę
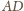 i równe
pola, więc też równe wysokości. Punkty
i równe
pola, więc też równe wysokości. Punkty
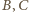 są po tej samej stronie
prostej
są po tej samej stronie
prostej
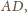 stąd
stąd
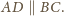 Dla pozostałych przekątnych dowód
jest analogiczny.
Dla pozostałych przekątnych dowód
jest analogiczny.
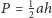
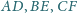 sześciokąta wypukłego
sześciokąta wypukłego
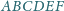 dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
dzieli go na dwa czworokąty o równych polach. Wykaż, że
trójkąty
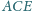 i
i
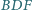 są podobne.
są podobne.
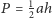
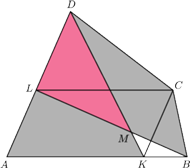
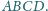 Punkty
Punkty
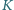 i
i
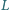 należą
odpowiednio do odcinków
należą
odpowiednio do odcinków
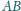 i
i
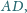 przy czym czworokąt
przy czym czworokąt
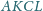 jest równoległobokiem. Odcinki
jest równoległobokiem. Odcinki
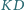 i
i
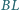 przecinają
się w punkcie
przecinają
się w punkcie
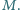 Wykaż, że
Wykaż, że
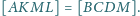
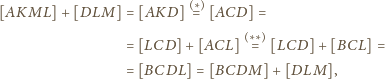
 wynika z równoległości
wynika z równoległości
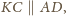 a
a
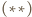 z
z
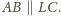
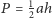
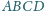 przecinają się w punkcie
przecinają się w punkcie
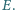 Wyznacz
Wyznacz
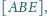 jeśli
jeśli
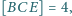
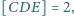
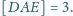
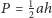
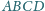 o podstawach
o podstawach
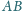 i
i
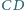 przecinają się
w punkcie
przecinają się
w punkcie
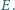 Dane są
Dane są
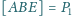 i
i
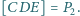 Wyznacz
Wyznacz
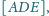
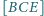 oraz
oraz
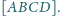
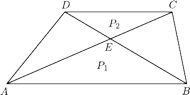
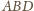 i
i
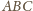 mają wspólną podstawę i równe
wysokości, więc też równe pola. Stąd
mają wspólną podstawę i równe
wysokości, więc też równe pola. Stąd
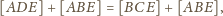
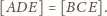
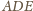 i
i
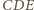 mają wspólną wysokość z
mają wspólną wysokość z
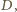 więc
więc
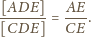
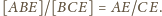 Stąd
Stąd
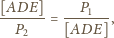
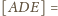
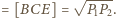 Wobec tego
Wobec tego
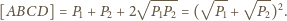
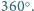
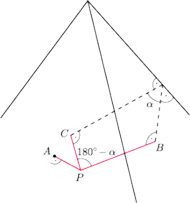
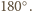
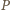 będzie
dowolnym punktem leżącym wewnątrz danego kąta trójściennego, a
będzie
dowolnym punktem leżącym wewnątrz danego kąta trójściennego, a
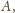
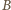 i
i
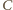 jego rzutami prostokątnymi na płaszczyzny
zawierające ściany danego kąta trójściennego. Jeśli
jego rzutami prostokątnymi na płaszczyzny
zawierające ściany danego kąta trójściennego. Jeśli
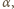
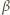 i
i
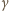 oznaczają miary kątów dwuściennych,
to miary kątów płaskich
oznaczają miary kątów dwuściennych,
to miary kątów płaskich
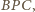
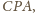
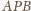 są równe
są równe
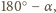
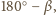
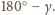
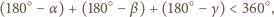
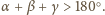
 jest środkiem sfery wpisanej w czworościan
jest środkiem sfery wpisanej w czworościan
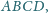 przy czym prosta
przy czym prosta
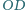 jest prostopadła do krawędzi
jest prostopadła do krawędzi
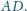 Znaleźć miarę kąta dwuściennego między płaszczyznami
Znaleźć miarę kąta dwuściennego między płaszczyznami
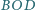 i
i
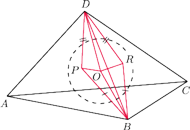
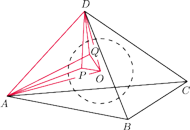
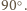 Niech
Niech
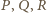 będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
będą
punktami styczności sfery wpisanej odpowiednio ze ścianami
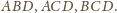 Z równości
Z równości
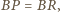
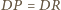 i
i
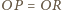 wnioskujemy, że czworościany
wnioskujemy, że czworościany
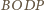 i
i
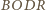 są przystające (
są przystające (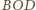 i
i
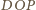 jest równy kątowi dwuściennemu
między płaszczyznami
jest równy kątowi dwuściennemu
między płaszczyznami
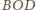 i
i
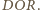 Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
Analogicznie dowodzimy, że
kąt dwuścienny między płaszczyznami
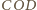 i
i
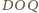 jest
równy kątowi dwuściennemu między płaszczyznami
jest
równy kątowi dwuściennemu między płaszczyznami
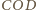 i
i
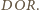 Wykażemy, że punkty
Wykażemy, że punkty
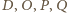 leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
leżą na jednej
płaszczyźnie. Wtedy, korzystając z poprzednich obserwacji, łatwo obliczyć, że
kąt dwuścienny między płaszczyznami
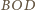 i
i
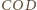 ma miarę
ma miarę
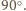
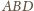 jest prostopadła do prostej
jest prostopadła do prostej
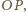 to
to
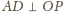 (
(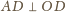 dostajemy
dostajemy
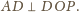 Analogicznie udowodnimy, że
Analogicznie udowodnimy, że
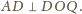 Zatem punkty
Zatem punkty
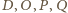 leżą na jednej
płaszczyźnie prostopadłej do krawędzi
leżą na jednej
płaszczyźnie prostopadłej do krawędzi
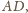 co kończy dowód.
co kończy dowód.