Jego Wysokości (II)»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Jego Wysokości (II)
- Publikacja w Delcie: październik 2020
- Publikacja elektroniczna: 30 września 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (374 KB)
Odcinki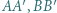 
i 
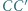są wysokościami trójkąta różnobocznego 
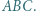Niech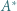 
oznacza punkt przecięcia prostych 
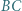i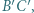 
analogicznie definiujemy punkty 
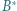i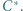 
Wykazać, że punkty 
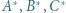leżą na prostej prostopadłej do prostej Eulera trójkąta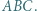 
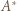Wskazówka
Potęgi punktu 
względem okręgów: 
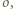okręgu o średnicy 
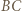oraz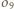 
są równe, więc punkt 
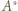leży na osi potęgowej okręgów 
i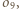 
czyli prostej prostopadłej do 
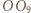(prostej Eulera). Analogicznie postępujemy z punktam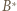i 
i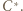 
(O potędze punktu względem okręgu można przeczytać w kąciku nr 11).