Składanie inwersji z symetrią»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Składanie inwersji z symetrią
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (390 KB)
Punkt 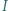 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 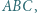 zaś
zaś  jest okręgiem opisanym na tym trójkącie. Okrąg
jest okręgiem opisanym na tym trójkącie. Okrąg 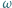 styczny do odcinków
styczny do odcinków 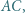
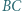 jest styczny do okręgu
jest styczny do okręgu  w punkcie
w punkcie 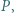 a
a 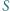 jest środkiem tego łuku
jest środkiem tego łuku 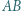 okręgu
okręgu 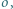 na którym leży punkt
na którym leży punkt 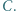 Wykazać, że punkty
Wykazać, że punkty 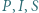 są współliniowe.
są współliniowe.

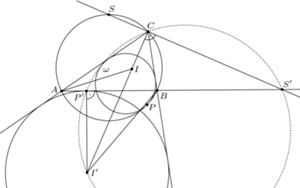
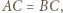 to punkty
to punkty 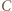 i
i 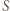 pokrywają się i punkty
pokrywają się i punkty 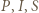 leżą na dwusiecznej
leżą na dwusiecznej 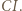 Dalej zakładamy, że
Dalej zakładamy, że 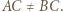 Wówczas punkty
Wówczas punkty 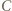 i
i 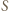 są różne, zaś proste
są różne, zaś proste 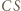 i
i 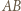 nie są równoległe. Rozważmy złożenie inwersji o środku
nie są równoległe. Rozważmy złożenie inwersji o środku 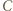 i promieniu
i promieniu 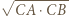 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 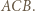 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 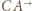 i
i 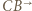 oraz prostą
oraz prostą 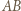 z okręgiem
z okręgiem 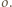 Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu
Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu 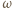 jest okrąg dopisany do trójkąta
jest okrąg dopisany do trójkąta 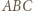 styczny do boku
styczny do boku 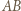 w punkcie
w punkcie 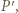 który jest obrazem punktu
który jest obrazem punktu 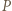 w tym przekształceniu. Ponieważ
w tym przekształceniu. Ponieważ 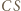 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 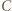 trójkąta
trójkąta 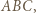 to proste
to proste 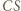 i
i 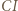 są prostopadłe. W takim razie obrazem punktu
są prostopadłe. W takim razie obrazem punktu 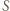 jest punkt
jest punkt 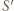 przecięcia prostej
przecięcia prostej 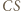 (która jest swoim własnym obrazem) z prostą
(która jest swoim własnym obrazem) z prostą 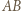 (która jest obrazem okręgu
(która jest obrazem okręgu  ). Niech
). Niech 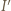 będzie obrazem punktu
będzie obrazem punktu 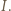 Wtedy z definicji inwersji mamy
Wtedy z definicji inwersji mamy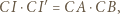
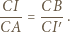
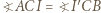 (bo inwersja zachowuje kąty) otrzymujemy, że trójkąty
(bo inwersja zachowuje kąty) otrzymujemy, że trójkąty 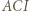 i
i 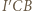 są podobne. W takim razie
są podobne. W takim razie 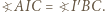 Ponieważ
Ponieważ 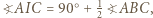 to mamy
to mamy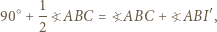
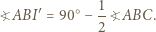
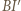 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 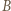 trójkąta
trójkąta 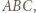 więc
więc 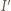 jest środkiem okręgu dopisanego do trójkąta
jest środkiem okręgu dopisanego do trójkąta 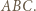 W takim razie
W takim razie 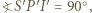 co wraz z równością
co wraz z równością 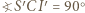 (bo
(bo 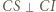 ) oznacza, że punkty
) oznacza, że punkty 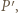
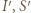 i
i 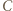 leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty
leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty 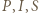 są współliniowe.
są współliniowe.