Nic nie może przecież wiecznie trwać»Zadanie 7
o zadaniu...
- Zadanie pochodzi z artykułu Nic nie może przecież wiecznie trwać
- Publikacja w Delcie: sierpień 2020
- Publikacja elektroniczna: 1 sierpnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)
Na tablicy napisano trzy nieujemne liczby całkowite. Wybieramy z tej trójki dwie liczby 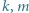 i zastępujemy je liczbami
i zastępujemy je liczbami 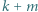 i
i 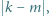 a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.
a trzecia liczba pozostaje bez zmiany. Z otrzymaną trójką postępujemy tak samo. Rozstrzygnąć, czy z każdej początkowej trójki liczb całkowitych nieujemnych można w ten sposób otrzymać trójkę, w której co najmniej dwie liczby są zerami.

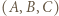 zapiszemy w postaci
zapiszemy w postaci 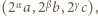 w której
w której 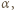
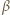 i
i 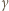 są całkowite nieujemne, zaś
są całkowite nieujemne, zaś 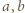 i
i  są nieparzyste lub równe
są nieparzyste lub równe 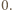 Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki
Jeśli w tej trójce jest najwyżej jedno zero, to stosując operacje z zadania, można doprowadzić do trójki 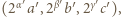 w której
w której 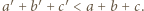 W tym celu przydatne są równości
W tym celu przydatne są równości 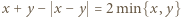 i
i 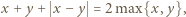 dzięki którym z trójki
dzięki którym z trójki 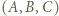 otrzymamy trójkę
otrzymamy trójkę