Jeżeli wszystkie wybrane punkty są białe, nie ma czego dowodzić. Przyjmijmy
więc, że tak nie jest. Ustalmy kierunek obiegu (orientację) okręgu; każdy łuk
ma wtedy początek i koniec.
Punkt biały nazwijmy fajnym, jeżeli każdy łuk okręgu, mający początek w tym
punkcie, zawiera więcej punktów białych niż czerwonych. Wybierzmy dowolną
parę punktów sąsiadujących, różnych kolorów, w której punkt biały jest
wcześniejszy niż punkt czerwony (bezpośrednio go poprzedza). Usuńmy tę
parę. Zauważmy, że wszystkie białe punkty, które nie były fajne, pozostają
niefajnymi w nowej sytuacji.
Powtarzamy to postępowanie, dopóki czerwone punkty nie znikną. Przyjmijmy,
że na starcie było
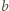 punktów białych oraz
punktów białych oraz
 czerwonych.
Po wykonaniu
czerwonych.
Po wykonaniu
 ruchów zostaje
ruchów zostaje
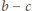 punktów, wszystkie białe,
oczywiście fajne (w tej końcowej sytuacji). One zatem były fajne już na
starcie; oznaczmy ich zbiór przez
punktów, wszystkie białe,
oczywiście fajne (w tej końcowej sytuacji). One zatem były fajne już na
starcie; oznaczmy ich zbiór przez
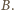
Zmieniamy orientację i powtarzamy rozumowanie. Otrzymujemy zbiór
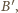 złożony z
złożony z
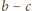 białych punktów, które już na starcie były
„fajne przy zmienionej orientacji”. Dla uzyskania tezy zadania należy
wykazać, że pewien punkt biały znajduje się w części wspólnej zbiorów
białych punktów, które już na starcie były
„fajne przy zmienionej orientacji”. Dla uzyskania tezy zadania należy
wykazać, że pewien punkt biały znajduje się w części wspólnej zbiorów
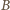 i
i
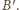 Do tego wystarczy, żeby zachodziła nierówność
Do tego wystarczy, żeby zachodziła nierówność
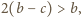 czyli
czyli
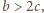 a to jest dane w założeniu.
a to jest dane w założeniu.
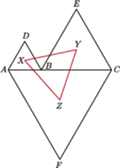
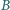 należy do odcinka
należy do odcinka 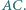 Punkty
Punkty 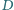 i
i 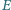 leżą po jednej stronie prostej
leżą po jednej stronie prostej 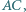 a punkt
a punkt 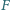 po drugiej, przy czym trójkąty
po drugiej, przy czym trójkąty 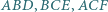 są równoboczne o ortocentrach odpowiednio
są równoboczne o ortocentrach odpowiednio 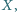
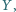
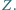 Udowodnić, że trójkąt
Udowodnić, że trójkąt 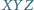 jest równoboczny.
jest równoboczny.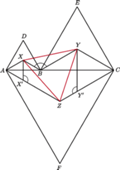
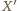 będzie takim punktem na odcinku
będzie takim punktem na odcinku 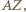 że
że 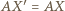 oraz niech
oraz niech 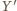 będzie takim punktem na odcinku
będzie takim punktem na odcinku 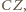 że
że 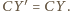
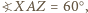 więc trójkąt
więc trójkąt 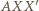 jest równoboczny. Podobnie trójkąt
jest równoboczny. Podobnie trójkąt 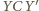 jest równoboczny. Zauważmy, że
jest równoboczny. Zauważmy, że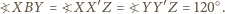
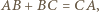 to
to 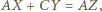 więc
więc 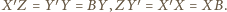 Zatem trójkąty
Zatem trójkąty 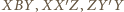 są przystające (cecha bkb). W szczególności
są przystające (cecha bkb). W szczególności 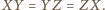
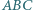 jest styczny do boków
jest styczny do boków 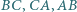 odpowiednio w punktach
odpowiednio w punktach 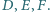 Udowodnij, że punkty
Udowodnij, że punkty 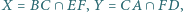
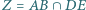 leżą na jednej prostej.
leżą na jednej prostej.
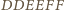 punkty
punkty 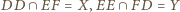 oraz
oraz 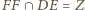 są współliniowe.
są współliniowe.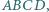 który nie jest trapezem, opisano okrąg. Wykaż, że punkty
który nie jest trapezem, opisano okrąg. Wykaż, że punkty 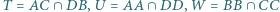 leżą na jednej prostej.
leżą na jednej prostej.
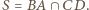 Z Twierdzenia Pascala dla sześciokąta
Z Twierdzenia Pascala dla sześciokąta 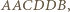 punkt
punkt 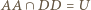 leży na prostej wyznaczonej przez punkty
leży na prostej wyznaczonej przez punkty 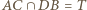 oraz
oraz 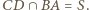 Z kolei z Twierdzenia Pascala dla
Z kolei z Twierdzenia Pascala dla 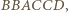 punkt
punkt 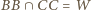 także leży na prostej wyznaczonej przez punkty
także leży na prostej wyznaczonej przez punkty 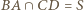 oraz
oraz 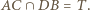
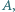
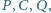
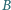 leżą w tej kolejności na łuku okręgu
leżą w tej kolejności na łuku okręgu 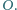 Na odcinkach
Na odcinkach 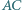 i
i 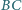 wybrano takie punkty odpowiednio
wybrano takie punkty odpowiednio 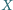 i
i 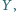 że
że 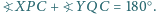 Wykaż, że wszystkie otrzymane w ten sposób proste
Wykaż, że wszystkie otrzymane w ten sposób proste 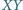 (przy ustalonych punktach
(przy ustalonych punktach 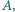
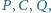
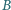 ) mają punkt wspólny.
) mają punkt wspólny.
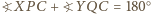 wynika, że punkt
wynika, że punkt 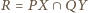 leży na okręgu
leży na okręgu 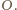 Z Twierdzenia Pascala dla sześciokąta
Z Twierdzenia Pascala dla sześciokąta 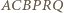 uzyskujemy współliniowość punktów
uzyskujemy współliniowość punktów 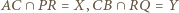 oraz niezależnego od
oraz niezależnego od 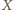 i
i 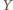 punktu
punktu 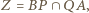 co kończy dowód.
co kończy dowód.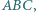 w którym
w którym 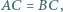 i takie punkty
i takie punkty 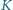 i
i 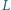 w jego wnętrzu, że
w jego wnętrzu, że 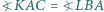 oraz
oraz 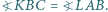 Udowodnij, że punkty
Udowodnij, że punkty 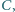
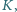
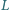 są współliniowe.
są współliniowe.
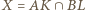 oraz
oraz 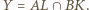 Z równoramienności trójkąta
Z równoramienności trójkąta 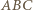 oraz danych równości kątów wynika, że
oraz danych równości kątów wynika, że 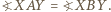 Ponieważ oba punkty
Ponieważ oba punkty 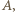
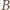 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 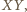 oznacza to, że punkty
oznacza to, że punkty 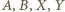 leżą na jednym okręgu.
leżą na jednym okręgu.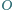 jest styczny do okręgu
jest styczny do okręgu 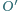 opisanego na trójkącie
opisanego na trójkącie 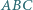 w punkcie
w punkcie 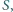 a do boków
a do boków 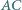 i
i 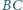 odpowiednio w punktach
odpowiednio w punktach 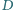 i
i 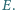 Wykaż, że środek okręgu wpisanego w trójkąt
Wykaż, że środek okręgu wpisanego w trójkąt 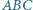 jest środkiem odcinka
jest środkiem odcinka 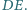
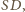
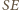 przecinają okrąg
przecinają okrąg 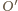 odpowiednio w drugich punktach
odpowiednio w drugich punktach 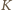 i
i 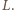 Warto rozważyć Twierdzenia Pascala dla sześciokąta
Warto rozważyć Twierdzenia Pascala dla sześciokąta 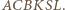
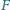 leży na boku
leży na boku 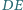 pięciokąta wypukłego
pięciokąta wypukłego 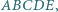 przy czym
przy czym 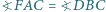 oraz
oraz 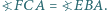 Wykaż, że
Wykaż, że 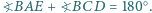
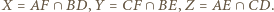
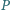 będzie pewnym wielościanem. Udowodnić, że istnieje stała
dodatnia
będzie pewnym wielościanem. Udowodnić, że istnieje stała
dodatnia
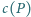 o następującej własności: jeśli pewnych
o następującej własności: jeśli pewnych
 kul
o sumie objętości
kul
o sumie objętości
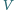 pokrywa wszystkie ściany (czyli każdy
punkt każdej ściany
pokrywa wszystkie ściany (czyli każdy
punkt każdej ściany
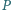 należy do co najmniej jednej z nich),
to
należy do co najmniej jednej z nich),
to
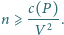
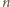 kul o promieniach
kul o promieniach
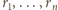 spełnia
podaną własność (pokrywa wszystkie ściany
spełnia
podaną własność (pokrywa wszystkie ściany
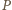 ). Wówczas
). Wówczas
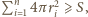 gdzie
gdzie
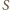 to pole powierzchni bocznej
to pole powierzchni bocznej
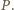 Ponadto
Ponadto
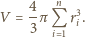
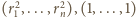 i wag
i wag
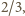
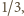 otrzymujemy
otrzymujemy
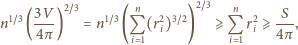
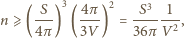
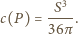
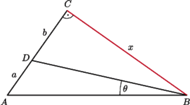
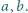 Rozważmy trójkąty prostokątne
Rozważmy trójkąty prostokątne
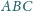 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku
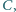 dla których
dla których
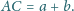 Niech
Niech
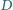 będzie punktem na
będzie punktem na
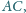 dla którego
dla którego
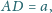
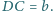 Znaleźć długość boku
Znaleźć długość boku
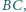 dla
której kąt
dla
której kąt
 jest maksymalny.
jest maksymalny.
 na dwa sposoby, mamy
na dwa sposoby, mamy
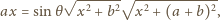
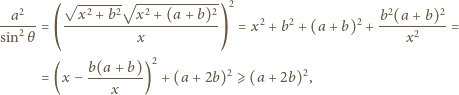
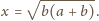 Kąt
Kąt
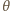 jest ostry, więc ma maksymalną wartość,
gdy
jest ostry, więc ma maksymalną wartość,
gdy
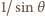 ma minimalną wartość, którą wyznaczyliśmy powyżej.
Zatem kąt
ma minimalną wartość, którą wyznaczyliśmy powyżej.
Zatem kąt
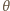 jest maksymalny dla
jest maksymalny dla
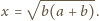
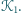 Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
Na jednym z jego boków, na zewnątrz,
zbudowano trzy sąsiadujące kolejno kwadraty
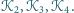 Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
Udowodnić,
że odcinki łączące odpowiednio środki kwadratów
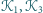 oraz
oraz
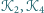 są prostopadłe.
są prostopadłe.
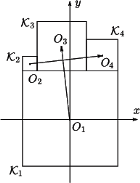
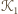 ma długość
ma długość
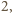 a kwadratów
a kwadratów
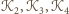 – odpowiednio
– odpowiednio
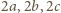 (stąd
(stąd
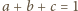 ).
Niech środek układu współrzędnych będzie ustawiony w środku
kwadratu
).
Niech środek układu współrzędnych będzie ustawiony w środku
kwadratu
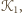 a osie niech będą równoległe do jego boków (jak na
rysunku). Oznaczmy środek kwadratu
a osie niech będą równoległe do jego boków (jak na
rysunku). Oznaczmy środek kwadratu
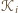 przez
przez
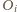 dla
dla
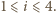
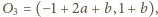 więc
więc
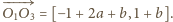 Podobnie,
skoro
Podobnie,
skoro
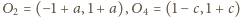 oraz
oraz
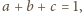 to otrzymujemy
to otrzymujemy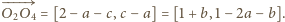 Stąd w oczywisty sposób
dostajemy
Stąd w oczywisty sposób
dostajemy
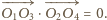
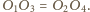
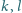 są styczne do okręgu
są styczne do okręgu
 w punktach
w punktach
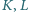 i przecinają
się w punkcie
i przecinają
się w punkcie
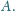 Punkt
Punkt
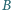 jest środkiem odcinka
jest środkiem odcinka
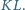 Wykazać, że punkty
Wykazać, że punkty
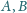 są symetryczne względem okręgu
są symetryczne względem okręgu
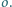
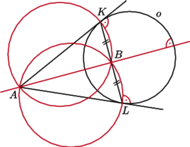
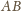 jest prostopadła do
jest prostopadła do
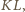 to jako bloki z definicji
można przyjąć okręgi o średnicach
to jako bloki z definicji
można przyjąć okręgi o średnicach
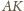 i
i
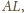 gdyż są
prostopadłe do
gdyż są
prostopadłe do
 i przechodzą przez
i przechodzą przez
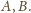 Oczywiście, sama
prosta
Oczywiście, sama
prosta
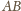 też się do tego celu nadaje.
też się do tego celu nadaje.
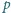 i
i
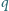 przecinają się w punktach
przecinają się w punktach
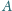 i
i
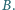 Prosta
Prosta
 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
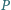 i
i
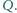 Punkt
Punkt
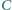 jest środkiem odcinka
jest środkiem odcinka
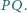 Wykazać,
że punkty
Wykazać,
że punkty
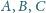 są współliniowe.
są współliniowe.

 będzie okręgiem o średnicy
będzie okręgiem o średnicy
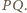 Okręgi
Okręgi
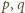 są
do niego prostopadłe, a zatem punkty
są
do niego prostopadłe, a zatem punkty
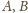 są symetryczne względem
są symetryczne względem
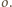 Stąd już wynika, że są współliniowe z punktem
Stąd już wynika, że są współliniowe z punktem
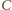 jako
środkiem tego okręgu – prosta poprowadzona z
jako
środkiem tego okręgu – prosta poprowadzona z
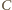 do punktu
do punktu
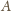 jest prostopadła do
jest prostopadła do
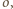 więc musi przechodzić przez punkt
więc musi przechodzić przez punkt
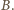
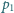 i
i
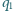 przecinają się w punktach
przecinają się w punktach
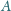 i
i
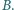 Prosta
Prosta
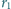 jest styczna do tych okręgów w punktach odpowiednio
jest styczna do tych okręgów w punktach odpowiednio
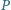 i
i
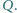 Punkt
Punkt
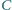 jest symetryczny do punktu
jest symetryczny do punktu
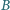 względem prostej
względem prostej
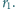 Okrąg
Okrąg
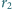 jest opisany na trójkącie
jest opisany na trójkącie
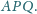 Proste
Proste
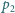 i
i
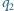 styczne do
styczne do
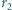 w punktach
odpowiednio
w punktach
odpowiednio
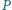 i
i
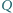 przecinają się w punkcie
przecinają się w punkcie
 Wykazać,
że punkty
Wykazać,
że punkty
 są współliniowe.
są współliniowe.
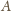 ; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
; obraz każdej z figur oznaczmy przez dodanie znaku prim. Na
podstawie własności 1 możemy zauważyć, że figury z zadania
zamieniły się rolami: okręgi
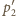 i
i
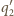 przecinają się w punktach
przecinają się w punktach
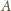 i
i
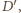 prosta
prosta
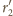 jest styczna do tych okręgów w punktach
jest styczna do tych okręgów w punktach
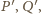 okrąg
okrąg
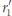 jest opisany na trójkącie
jest opisany na trójkącie
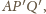 proste
proste
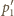 i
i
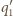 są styczne do
są styczne do
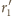 w punktach
w punktach
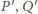 oraz
przecinają się w punkcie
oraz
przecinają się w punkcie
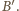
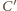 jest symetryczny do punktu
jest symetryczny do punktu
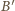 względem okręgu
względem okręgu
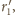 co na mocy zadania 1 oznacza, że jest
środkiem odcinka
co na mocy zadania 1 oznacza, że jest
środkiem odcinka
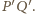 W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
W ten sposób otrzymaliśmy konfigurację
z zadania 2, a zatem punkty
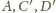 są współliniowe. Obrazem prostej
są współliniowe. Obrazem prostej
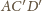 jest prosta
jest prosta
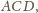 co kończy rozwiązanie.
co kończy rozwiązanie.
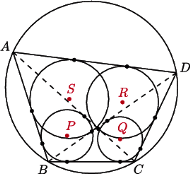
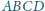 jest wpisany w okrąg. W trójkąty
jest wpisany w okrąg. W trójkąty
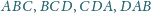 wpisano okręgi. Wykazać, że środki
wpisano okręgi. Wykazać, że środki
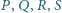 tych okręgów są wierzchołkami prostokąta.
tych okręgów są wierzchołkami prostokąta.
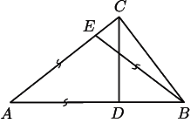
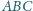 o przeciwprostokątnej
o przeciwprostokątnej
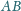 punkt
punkt
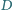 jest spodkiem wysokości opuszczonej
z wierzchołka
jest spodkiem wysokości opuszczonej
z wierzchołka
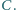 Wyznaczyć stosunek
Wyznaczyć stosunek
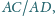 jeśli
wiadomo, że okrąg o środku
jeśli
wiadomo, że okrąg o środku
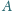 i promieniu
i promieniu
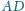 oraz
okrąg o środku
oraz
okrąg o środku
 i tym samym promieniu przecinają się
w punkcie
i tym samym promieniu przecinają się
w punkcie
 na przyprostokątnej
na przyprostokątnej
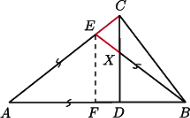
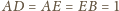 i oznaczmy punkt przecięcia
odcinków
i oznaczmy punkt przecięcia
odcinków
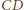 i
i
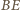 przez
przez
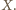 Niech
Niech
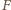 będzie
rzutem prostokątnym punktu
będzie
rzutem prostokątnym punktu
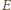 na odcinek
na odcinek
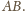
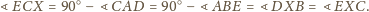
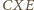 jest równoramienny, oznaczmy
jest równoramienny, oznaczmy
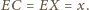 Z twierdzenia Pitagorasa mamy
Z twierdzenia Pitagorasa mamy
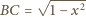
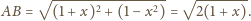
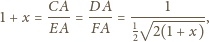
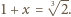 Zatem
Zatem
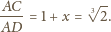
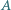 i
i 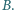 Punkt
Punkt 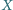 leży na jednym z tych okręgów, punkt
leży na jednym z tych okręgów, punkt 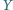 na drugim, przy czym prosta
na drugim, przy czym prosta 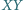 nie przechodzi ani przez
nie przechodzi ani przez 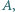 ani przez
ani przez 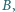 ani przez środek odcinka
ani przez środek odcinka 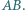 Punkt
Punkt 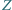 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 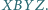 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 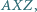
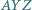 są przystające do dwóch danych okręgów.
są przystające do dwóch danych okręgów.
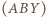 przez
przez 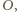 środek okręgu
środek okręgu 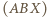 przez
przez 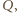 i niech
i niech 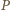 będzie punktem symetrycznym do
będzie punktem symetrycznym do 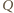 względem prostej
względem prostej 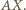 Czworokąty
Czworokąty 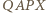 i
i 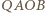 są rombami. Zatem
są rombami. Zatem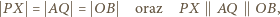
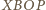 jest równoległobokiem. Również czworokąt
jest równoległobokiem. Również czworokąt 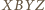 jest (z założenia) równoległobokiem. Stąd - jak przed chwilą - wnosimy, że równoległobokiem jest także czworokąt
jest (z założenia) równoległobokiem. Stąd - jak przed chwilą - wnosimy, że równoległobokiem jest także czworokąt 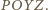 Wobec tego
Wobec tego 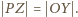
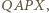 pokazuje, że odległość punktu
pokazuje, że odległość punktu 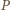 od każdego z trójki punktów
od każdego z trójki punktów 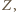
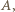
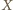 jest równa promieniowi dwóch danych okręgów. Inaczej mówiąc,
jest równa promieniowi dwóch danych okręgów. Inaczej mówiąc, 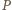 jest środkiem okręgu przystającego do nich i przechodzącego przez punkty
jest środkiem okręgu przystającego do nich i przechodzącego przez punkty 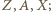 to jest pierwsza część tezy. Druga część tezy, dotycząca okręgu opisanego na trójkącie
to jest pierwsza część tezy. Druga część tezy, dotycząca okręgu opisanego na trójkącie  wynika z pierwszej przez symetrię (logiczną).
wynika z pierwszej przez symetrię (logiczną).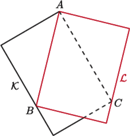
 i
i
 niekoniecznie o tych samych
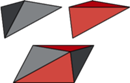
wymiarach, położono jak na rysunku. Czy kartka
niekoniecznie o tych samych
wymiarach, położono jak na rysunku. Czy kartka
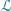 przykrywa ponad
połowę kartki
przykrywa ponad
połowę kartki
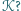
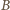 i
i
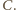 Kartka
Kartka
 przykrywa
cały trójkąt
przykrywa
cały trójkąt
 i jeszcze kawałek kartki
i jeszcze kawałek kartki
 – łącznie ponad
połowę.
– łącznie ponad
połowę.
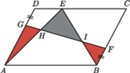
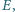
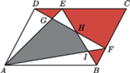
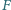 i
i
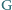 należą odpowiednio
do boków
należą odpowiednio
do boków
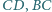 i
i
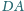 równoległoboku
równoległoboku
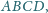 przy czym
przy czym
 Odcinek
Odcinek
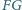 przecina odcinki
przecina odcinki
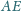 i
i
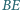 odpowiednio w punktach
odpowiednio w punktach
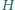 i
i
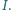 Wykaż,
że
Wykaż,
że
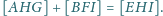
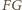 dzieli równoległobok
dzieli równoległobok
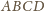 na dwie figury
przystające. Wobec tego i na mocy twierdzenia (*), mamy
na dwie figury
przystające. Wobec tego i na mocy twierdzenia (*), mamy
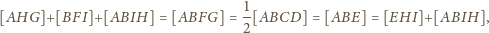
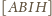 daje tezę.
daje tezę.
 należy do boku
należy do boku
 równoległoboku
równoległoboku
 punkt
punkt
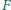 – do boku
– do boku
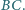 Odcinek
Odcinek
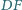 przecina odcinki
przecina odcinki
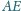 i
i
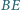 odpowiednio w punktach
odpowiednio w punktach
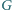 i
i
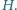 Odcinki
Odcinki
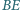 i
i
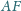 przecinają się
w punkcie
przecinają się
w punkcie
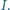 Wykaż, że
Wykaż, że
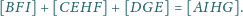
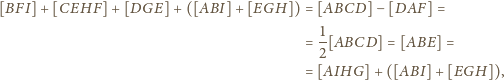
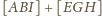 daje tezę.
daje tezę.
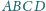 oraz punkt
oraz punkt
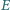 należący do boku
należący do boku
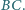 Przez punkt
Przez punkt
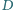 prowadzimy prostą
prowadzimy prostą
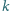 równoległą
do prostej
równoległą
do prostej
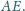 Na prostej
Na prostej
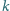 obieramy takie punkty
obieramy takie punkty
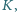
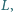 że czworokąt
że czworokąt
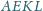 jest równoległobokiem. Udowodnij, że
równoległoboki
jest równoległobokiem. Udowodnij, że
równoległoboki
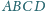 i
i
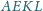 mają równe pola.
mają równe pola.
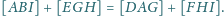
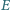 należy do boku
należy do boku
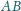 równoległoboku
równoległoboku
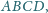 punkt
punkt
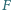 – do boku
– do boku
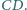 Odcinki
Odcinki
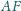 i
i
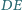 przecinają się w punkcie
przecinają się w punkcie
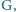 odcinki
odcinki
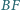 i
i
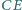 przecinają się w punkcie
przecinają się w punkcie
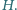 Wykaż,
że
Wykaż,
że

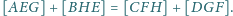

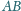 i liczba dodatnia
i liczba dodatnia
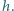 Wśród
trójkątów
Wśród
trójkątów
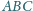 o podstawie
o podstawie
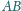 i wysokości opuszczonej
z wierzchołka
i wysokości opuszczonej
z wierzchołka
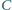 długości
długości
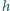 znaleźć taki, dla którego iloczyn
długości wszystkich trzech wysokości jest maksymalny.
znaleźć taki, dla którego iloczyn
długości wszystkich trzech wysokości jest maksymalny.
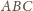 o wysokości opuszczonej
z wierzchołka
o wysokości opuszczonej
z wierzchołka
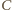 długości
długości
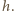 Oznaczmy długości wysokości
opuszczonych z wierzchołków
Oznaczmy długości wysokości
opuszczonych z wierzchołków
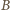 i
i
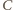 odpowiednio
przez
odpowiednio
przez
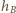 i
i
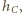 a jego pole przez
a jego pole przez
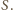 Wiemy, że
Wiemy, że
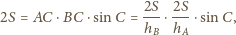
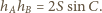
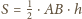 jest ustalone, to iloczyn
jest ustalone, to iloczyn
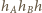 jest maksymalny wtedy i tylko wtedy, gdy
jest maksymalny wtedy i tylko wtedy, gdy
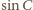 ma
maksymalną wartość. Oczywiście, kąt
ma
maksymalną wartość. Oczywiście, kąt
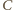 ma maksymalną wartość
(oznaczmy ją przez
ma maksymalną wartość
(oznaczmy ją przez
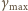 ), gdy
), gdy
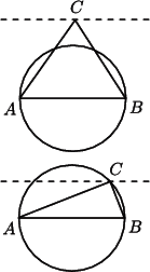
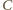 jest wierzchołkiem trójkąta
równoramiennego o podstawie
jest wierzchołkiem trójkąta
równoramiennego o podstawie
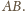 Jeśli
Jeśli
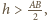 to
to
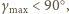 więc rozwiązaniem jest trójkąt równoramienny
o podstawie
więc rozwiązaniem jest trójkąt równoramienny
o podstawie
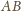 i wysokości
i wysokości
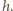
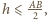 to
to
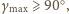 więc rozwiązaniem
jest trójkąt prostokątny o przeciwprostokątnej
więc rozwiązaniem
jest trójkąt prostokątny o przeciwprostokątnej
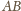 (dla którego
(dla którego
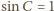 ).
).
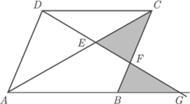
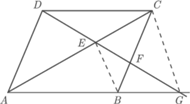
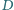 równoległoboku
równoległoboku
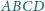 przecina jego przekątną
przecina jego przekątną
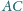 w punkcie
w punkcie
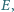 bok
bok
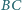 w punkcie
w punkcie
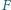 i przedłużenie boku
i przedłużenie boku
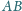 w punkcie
w punkcie
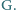 Pola trójkątów
Pola trójkątów
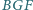 i
i
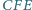 są równe. Wyznaczyć
stosunek długości odcinków
są równe. Wyznaczyć
stosunek długości odcinków
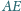 i
i
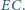
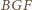 i
i
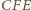 mają równe pola, to także
trójkąty
mają równe pola, to także
trójkąty
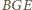 i
i
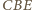 mają równe pola, więc ich wysokości
opuszczone na wspólną podstawę
mają równe pola, więc ich wysokości
opuszczone na wspólną podstawę
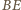 są równej długości, a stąd
są równej długości, a stąd
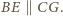 Niech
Niech
 oznacza szukany stosunek. Z twierdzenia
Talesa dostajemy kolejno
oznacza szukany stosunek. Z twierdzenia
Talesa dostajemy kolejno
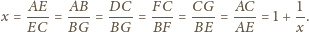
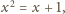 skąd
skąd
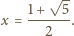
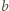 punktów białych oraz
punktów białych oraz
 czerwonych.
Po wykonaniu
czerwonych.
Po wykonaniu
 ruchów zostaje
ruchów zostaje
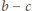 punktów, wszystkie białe,
oczywiście fajne (w tej końcowej sytuacji). One zatem były fajne już na
starcie; oznaczmy ich zbiór przez
punktów, wszystkie białe,
oczywiście fajne (w tej końcowej sytuacji). One zatem były fajne już na
starcie; oznaczmy ich zbiór przez
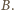
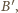 złożony z
złożony z
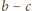 białych punktów, które już na starcie były
„fajne przy zmienionej orientacji”. Dla uzyskania tezy zadania należy
wykazać, że pewien punkt biały znajduje się w części wspólnej zbiorów
białych punktów, które już na starcie były
„fajne przy zmienionej orientacji”. Dla uzyskania tezy zadania należy
wykazać, że pewien punkt biały znajduje się w części wspólnej zbiorów
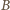 i
i
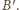 Do tego wystarczy, żeby zachodziła nierówność
Do tego wystarczy, żeby zachodziła nierówność
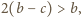 czyli
czyli
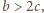 a to jest dane w założeniu.
a to jest dane w założeniu.
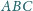 przecinają okrąg na nim
opisany odpowiednio w punktach
przecinają okrąg na nim
opisany odpowiednio w punktach
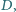
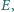
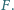 Odcinki prostych
Odcinki prostych
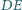 i
i
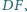 wyznaczone przez punkty przecięcia tych prostych
z bokami trójkąta, mają środki w punktach
wyznaczone przez punkty przecięcia tych prostych
z bokami trójkąta, mają środki w punktach
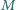 i
i
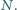 Odcinki
Odcinki
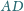 i
i
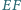 przecinają się w punkcie
przecinają się w punkcie
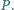 Wykazać, że
środek okręgu, przechodzącego przez punkty
Wykazać, że
środek okręgu, przechodzącego przez punkty
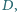
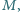
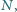 leży
na okręgu, przechodzącym przez punkty
leży
na okręgu, przechodzącym przez punkty
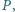
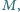
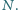
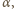
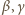 miary kątów trójkąta
miary kątów trójkąta
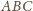 przy
wierzchołkach
przy
wierzchołkach
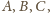 zaś przez
zaś przez
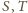 punkty przecięcia
odcinka
punkty przecięcia
odcinka
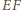 odpowiednio z bokami
odpowiednio z bokami
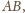
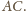 Odcinki
Odcinki
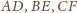 przecinają się w punkcie
przecinają się w punkcie
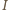 (środku okręgu
wpisanego). Z równości
(środku okręgu
wpisanego). Z równości
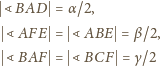
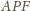 kąty przy wierzchołkach
kąty przy wierzchołkach
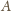 i
i
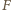 sumują się do kąta prostego. Zatem kąt przy
wierzchołku
sumują się do kąta prostego. Zatem kąt przy
wierzchołku
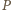 jest prosty. W trójkącie
jest prosty. W trójkącie
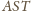 odcinek
odcinek
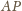 jest więc jednocześnie dwusieczną i wysokością; to znaczy, że
punkt
jest więc jednocześnie dwusieczną i wysokością; to znaczy, że
punkt
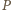 jest środkiem odcinka
jest środkiem odcinka
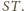
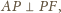 równość
równość
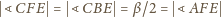
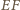 jest symetralną odcinka
jest symetralną odcinka
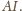 Przez analogię,
punkty
Przez analogię,
punkty
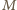 i
i
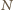 są środkami odcinków
są środkami odcinków
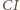 i
i
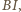 a proste
a proste
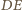 i
i
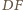 są symetralnymi tych odcinków. W takim razie
jednokładność o środku
są symetralnymi tych odcinków. W takim razie
jednokładność o środku
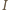 i skali
i skali
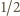 przekształca trójkąt
przekształca trójkąt
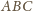 na trójkąt
na trójkąt
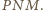
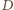 jest środek
jest środek
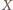 odcinka
odcinka
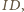 który
wobec tego leży na okręgu
który
wobec tego leży na okręgu
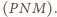 Pozostaje zauważyć, że
punkt
Pozostaje zauważyć, że
punkt
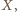 jako środek przeciwprostokątnej trójkątów prostokątnych
jako środek przeciwprostokątnej trójkątów prostokątnych
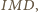
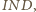 jest też środkiem okręgu
jest też środkiem okręgu
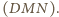

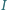 będzie środkiem okręgu wpisanego w trójkąt
będzie środkiem okręgu wpisanego w trójkąt
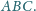 Półproste
Półproste
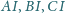 przecinają okrąg opisany na
nim odpowiednio w punktach
przecinają okrąg opisany na
nim odpowiednio w punktach
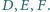 Udowodnić, że proste
Udowodnić, że proste
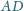 i
i
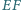 są prostopadłe.
są prostopadłe.

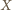 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych
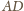 i
i
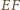 oraz
oraz
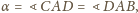
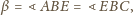
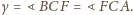
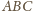 otrzymujemy
otrzymujemy
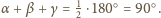 Ponadto kąty
Ponadto kąty
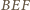 i
i
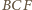 są oparte na tym samym łuku, a stąd
są oparte na tym samym łuku, a stąd
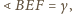 natomiast kąt
natomiast kąt
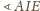 jako kąt zewnętrzny trójkąta
jako kąt zewnętrzny trójkąta
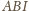 ma miarę
ma miarę
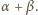 W takim razie
W takim razie
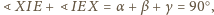 więc
trójkąt
więc
trójkąt
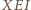 jest prostokątny.
jest prostokątny.
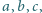 o wszystkich kątach
wewnętrznych mniejszych od
o wszystkich kątach
wewnętrznych mniejszych od
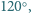 znajduje się punkt, którego suma
odległości od wierzchołków jest minimalna i wynosi
znajduje się punkt, którego suma
odległości od wierzchołków jest minimalna i wynosi
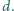 Dowieść,
że zachodzi równość
Dowieść,
że zachodzi równość

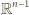 umieścimy sympleks foremny
o krawędzi
umieścimy sympleks foremny
o krawędzi
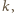 to dla dowolnego punktu tej przestrzeni, leżącego
w odległościach
to dla dowolnego punktu tej przestrzeni, leżącego
w odległościach
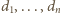 od jego wierzchołków, zachodzi
równość
od jego wierzchołków, zachodzi
równość
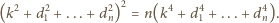
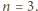
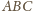 będzie trójkątem rozważanym obecnie, o bokach
będzie trójkątem rozważanym obecnie, o bokach
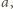
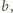
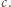 Punkt, o którym mowa, to punkt Toricellego (lub punkt
Fermata)
Punkt, o którym mowa, to punkt Toricellego (lub punkt
Fermata)
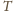 ; założenie o kątach
; założenie o kątach
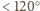 gwarantuje, że
gwarantuje, że
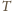 leży wewnątrz trójkąta, na przecięciu odcinków
leży wewnątrz trójkąta, na przecięciu odcinków
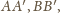
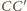 – gdzie litery z primami oznaczają wierzchołki trójkątów
równobocznych
– gdzie litery z primami oznaczają wierzchołki trójkątów
równobocznych
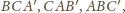 zbudowanych na zewnątrz trójkąta
zbudowanych na zewnątrz trójkąta
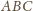 – to własność dobrze znana (wyprowadzenie i komentarze można
znaleźć w wielu miejscach; choćby http://pl.wikipedia.org/wiki/Punkt_Fermata).
– to własność dobrze znana (wyprowadzenie i komentarze można
znaleźć w wielu miejscach; choćby http://pl.wikipedia.org/wiki/Punkt_Fermata).
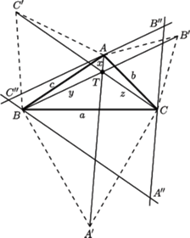
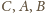 prowadzimy proste równoległe odpowiednio do
prowadzimy proste równoległe odpowiednio do
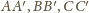 ; przecinając się, tworzą one trójkąt równoboczny
; przecinając się, tworzą one trójkąt równoboczny
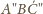 (oznaczenia jak na rysunku). W trapezach równoramiennych
(o kątach
(oznaczenia jak na rysunku). W trapezach równoramiennych
(o kątach
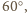
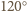 )
)
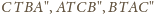 zachodzą
równości
zachodzą
równości
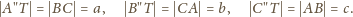
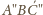 ma bok długości
ma bok długości
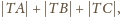 czyli
czyli
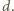
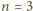 ) do trójkąta
) do trójkąta
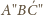 oraz punktu
oraz punktu
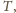 leżącego w odległościach
leżącego w odległościach
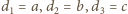 od
od
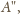
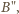
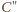 ; teraz
; teraz
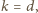 i mamy tezę zadania.
i mamy tezę zadania.