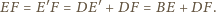Zadanie ZM-13.10-KP-5
o zadaniu...
- Publikacja w Delcie: październik 2013
- Publikacja elektroniczna: 01-10-2013
Dany jest czworościan
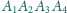 i punkty
i punkty
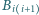 leżące na
krawędziach
leżące na
krawędziach
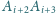 dla
dla
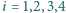 przyjmujemy, że
przyjmujemy, że
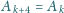 ). Każda z płaszczyzn
). Każda z płaszczyzn
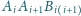 tworzy z płaszczyzną
tworzy z płaszczyzną
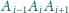 kąt dwuścienny o mierze
kąt dwuścienny o mierze
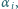 zaś z płaszczyzną
zaś z płaszczyzną
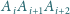 kąt dwuścienny o mierze
kąt dwuścienny o mierze
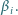 Wykazać, że
płaszczyzny
Wykazać, że
płaszczyzny
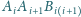 dla
dla
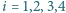 mają wspólny punkt
wtedy i tylko wtedy, gdy
mają wspólny punkt
wtedy i tylko wtedy, gdy
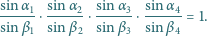 |
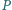 leży wewnątrz czworościanu
leży wewnątrz czworościanu
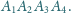 Wykazać, że
płaszczyzny symetryczne do płaszczyzn
Wykazać, że
płaszczyzny symetryczne do płaszczyzn
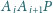 względem płaszczyzn
dwusiecznych kątów dwuściennych przy krawędziach
względem płaszczyzn
dwusiecznych kątów dwuściennych przy krawędziach
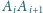 dla
dla
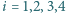 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
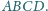 Punkty
Punkty
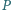 i
i
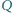 leżą
odpowiednio na bokach
leżą
odpowiednio na bokach
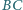 i
i
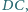 odcinki
odcinki
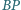 i
i
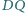 mają
jednakową długość. Dowieść, że odcinki
mają
jednakową długość. Dowieść, że odcinki
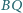 i
i
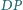 przecinają
się w punkcie, leżącym na dwusiecznej kąta
przecinają
się w punkcie, leżącym na dwusiecznej kąta
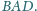

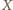 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków
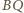 i
i
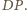 Przedłużamy
odcinek
Przedłużamy
odcinek
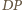 do przecięcia z prostą
do przecięcia z prostą
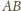 w punkcie
w punkcie
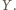 Z równoległości
Z równoległości
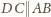 oraz
oraz
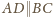 wynikają
proporcje
wynikają
proporcje

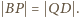 Zatem i lewe strony mają jednakową wartość; a to znaczy,
że w trójkącie
Zatem i lewe strony mają jednakową wartość; a to znaczy,
że w trójkącie
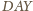 odcinek
odcinek
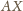 jest dwusieczną kąta przy
wierzchołku
jest dwusieczną kąta przy
wierzchołku
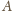 (czy go nazwiemy
(czy go nazwiemy
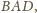 czy
czy
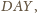 to
wszystko jedno).
to
wszystko jedno).

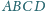 jest wpisany w okrąg. Styczne do okręgu w punktach
jest wpisany w okrąg. Styczne do okręgu w punktach
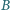 i
i
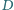 przecinają się w punkcie
przecinają się w punkcie
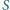 (rysunek). Udowodnić,
że punkt
(rysunek). Udowodnić,
że punkt
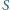 leży na prostej
leży na prostej
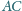 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
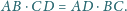

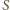 leży na prostej
leży na prostej
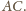
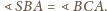 Zatem trójkąty
Zatem trójkąty
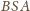 i
i
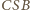 są podobne, więc
są podobne, więc
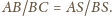 Podobnie
stwierdzimy, że
Podobnie
stwierdzimy, że
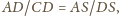 ale
ale
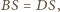 więc
więc
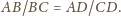

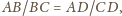 ale
ale
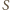 nie leży na
nie leży na
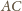 (powiedzmy, że punkt
(powiedzmy, że punkt
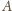 leży bliżej punktu
leży bliżej punktu
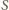 niż
punkt
niż
punkt
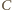 ).
).
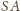 przecina okrąg w punkcie
przecina okrąg w punkcie
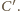 Z poprzedniej części zadania
wiadomo, że
Z poprzedniej części zadania
wiadomo, że
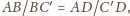 więc
więc
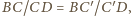 co
wraz z równością kątów
co
wraz z równością kątów
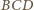 i
i
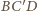 implikuje, że trójkąty
implikuje, że trójkąty
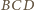 i
i
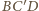 są podobne, a że mają wspólny bok, to są
przystające. Zatem
są podobne, a że mają wspólny bok, to są
przystające. Zatem
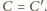
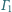 i
i
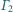 są rozłączne zewnętrznie, a ich wspólne
styczne zewnętrzne przecinają się w punkcie
są rozłączne zewnętrznie, a ich wspólne
styczne zewnętrzne przecinają się w punkcie
 Okrąg
Okrąg
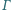 jest
styczny zewnętrznie do okręgów
jest
styczny zewnętrznie do okręgów
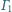 i
i
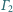 odpowiednio
w punktach
odpowiednio
w punktach
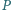 i
i
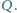 Wykaż, że punkty
Wykaż, że punkty
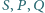 są
współliniowe.
są
współliniowe.

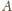 i
i
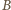 będą punktami styczności okręgów odpowiednio
będą punktami styczności okręgów odpowiednio
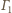 i
i
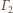 do jednej z danych prostych. Rozważmy inwersję
względem okręgu o środku
do jednej z danych prostych. Rozważmy inwersję
względem okręgu o środku
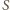 i promieniu
i promieniu
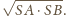 Obie
rozpatrywane proste styczne są stałe, bo przechodzą przez środek inwersji
Obie
rozpatrywane proste styczne są stałe, bo przechodzą przez środek inwersji
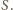 Punkt
Punkt
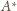 leży na półprostej
leży na półprostej
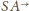 i spełnia warunek
i spełnia warunek
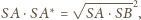 stąd
stąd
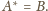 Obrazem okręgu
Obrazem okręgu
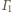 jest
okrąg (bo
jest
okrąg (bo
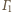 nie przechodzi przez punkt
nie przechodzi przez punkt
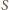 ), styczny do danych
prostych (bo są one stałe) i przechodzący przez punkt
), styczny do danych
prostych (bo są one stałe) i przechodzący przez punkt
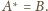 Wobec tego
Wobec tego
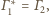 stąd także
stąd także
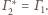
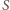 leży na zewnątrz okręgu
leży na zewnątrz okręgu
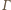 ; niech
; niech
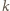 i
i
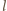 będą
prostymi stycznymi do
będą
prostymi stycznymi do
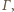 poprowadzonymi z
poprowadzonymi z
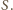 Obrazem
Obrazem
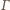 jest okrąg styczny do
jest okrąg styczny do
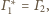
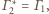
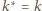 oraz
oraz
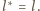 Jedynym takim okręgiem jest właśnie
Jedynym takim okręgiem jest właśnie
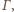 czyli
czyli
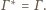
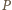 to punkt styczności
to punkt styczności
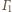 i
i
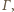 więc jego obrazem jest
punkt styczności
więc jego obrazem jest
punkt styczności
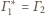 i
i
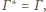 czyli
czyli
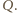 Środek
inwersji
Środek
inwersji
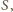 punkt
punkt
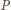 i jego obraz
i jego obraz
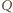 są współliniowe.
są współliniowe.
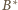 zamiast
zamiast
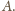
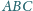 o podstawie
o podstawie
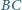 i okrąg
i okrąg
 opisany na tym trójkącie. Okrąg
opisany na tym trójkącie. Okrąg
 jest styczny do prostej
jest styczny do prostej
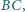 ale nie do odcinka
ale nie do odcinka
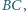 oraz do tego łuku
oraz do tego łuku
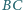 okręgu
okręgu
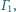 do którego należy punkt
do którego należy punkt
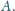 Prosta
Prosta
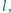 przechodząca przez
punkt
przechodząca przez
punkt
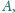 jest styczna do okręgu
jest styczna do okręgu
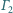 w punkcie
w punkcie
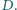 Wykaż,
że
Wykaż,
że

 i promieniu
i promieniu
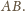 Obrazem okręgu
Obrazem okręgu
 przechodzącego przez środek inwersji
przechodzącego przez środek inwersji
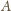 oraz przez punkty
oraz przez punkty
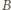 i
i
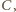 jest prosta przez punkty
jest prosta przez punkty
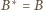 i
i
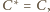 czyli prosta
czyli prosta
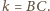 Stąd też
Stąd też
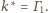
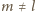 będzie prostą przechodzącą przez punkt
będzie prostą przechodzącą przez punkt
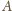 i styczną
do
i styczną
do
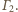 Obrazem okręgu
Obrazem okręgu
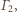 nieprzechodzącego przez środek
inwersji, jest okrąg styczny do
nieprzechodzącego przez środek
inwersji, jest okrąg styczny do
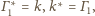
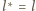 oraz
oraz
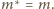 Jedynym takim okręgiem jest
Jedynym takim okręgiem jest
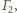 stąd
stąd
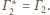
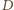 to punkt styczności prostej
to punkt styczności prostej
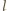 i okręgu
i okręgu
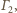 więc
jego obrazem jest punkt styczności
więc
jego obrazem jest punkt styczności
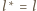 oraz
oraz
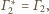 czyli on
sam:
czyli on
sam:
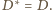 Wobec tego z warunku
Wobec tego z warunku
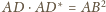 wynika, że
wynika, że
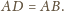
 zamiast
zamiast
 są styczne wewnętrznie do okręgu
są styczne wewnętrznie do okręgu
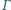 odpowiednio
w punktach
odpowiednio
w punktach
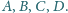 Ponadto okręgi
Ponadto okręgi
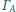 i
i
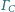 są styczne
zewnętrznie do obu okręgów
są styczne
zewnętrznie do obu okręgów
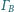 i
i
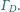 Proste styczne do
okręgu
Proste styczne do
okręgu
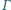 w punktach
w punktach
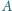 i
i
 przecinają się w punkcie
przecinają się w punkcie
 Udowodnij, że punkty
Udowodnij, że punkty
 leżą na jednej prostej.
leżą na jednej prostej.
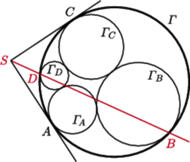
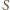 i promieniu
i promieniu
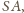 okręgi
okręgi
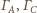 i
i
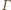 są stałe. Stąd
są stałe. Stąd
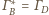 oraz
oraz
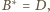 co daje
tezę.
co daje
tezę.
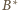 zamiast
zamiast
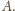
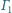 i
i
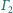 są styczne zewnętrznie i styczne do prostej
są styczne zewnętrznie i styczne do prostej
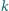 odpowiednio w punktach
odpowiednio w punktach
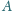 i
i
 Odcinek
Odcinek
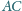 jest
średnicą okręgu
jest
średnicą okręgu
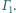 Prosta
Prosta
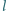 przechodzi przez punkt
przechodzi przez punkt
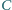 i jest styczna do okręgu
i jest styczna do okręgu
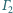 w punkcie
w punkcie
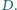 Wykaż, że
Wykaż, że
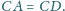
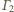 jest stały przy inwersji względem
jest stały przy inwersji względem
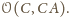


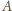 oznacza podzbiór wszystkich pokolorowanych punktów
na okręgu, zaś
oznacza podzbiór wszystkich pokolorowanych punktów
na okręgu, zaś
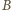 niech oznacza podzbiór wszystkich tych
punktów, których antypody są pokolorowane. Chcemy udowodnić, że
niech oznacza podzbiór wszystkich tych
punktów, których antypody są pokolorowane. Chcemy udowodnić, że
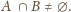 Załóżmy przeciwnie, że są rozłączne. W tej sytuacji
Załóżmy przeciwnie, że są rozłączne. W tej sytuacji
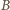 składa się z odcinków o łącznej długości takiej jak
składa się z odcinków o łącznej długości takiej jak
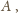 więc
łączna długość odcinków składających się na sumę
więc
łączna długość odcinków składających się na sumę
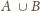 jest większa
niż obwód okręgu, co daje sprzeczność.
jest większa
niż obwód okręgu, co daje sprzeczność.
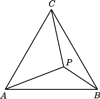
 wewnątrz trójkąta równobocznego
wewnątrz trójkąta równobocznego
 Udowodnić, że
Udowodnić, że
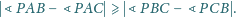
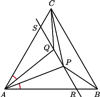
 Odbijmy
symetrycznie
Odbijmy
symetrycznie
 względem dwusiecznej kąta
względem dwusiecznej kąta
 otrzymując punkt
otrzymując punkt
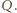 Niech
Niech
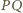 przecina
przecina
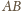 i
i
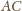 odpowiednio
w punktach
odpowiednio
w punktach
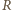 i
i
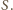 Oczywiście
Oczywiście
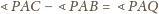
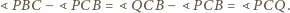
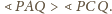 Rozważmy obraz
Rozważmy obraz
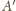 punktu
punktu
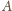 przy symetrii względem
przy symetrii względem
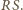 Zauważmy, że punkt
Zauważmy, że punkt
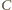 leży na zewnątrz okręgu opisanego na trójkącie równobocznym
leży na zewnątrz okręgu opisanego na trójkącie równobocznym
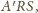 gdyż
gdyż
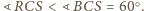 W szczególności, punkt
W szczególności, punkt
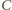 leży na zewnątrz okręgu opisanego na trójkącie
leży na zewnątrz okręgu opisanego na trójkącie
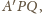 gdyż
ten okrąg leży wewnątrz poprzedniego. Stąd
gdyż
ten okrąg leży wewnątrz poprzedniego. Stąd
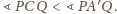
 trójkąta równoramiennego
trójkąta równoramiennego
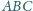 o podstawie
o podstawie
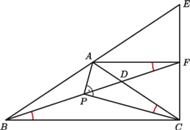
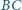 dany jest punkt
dany jest punkt
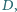 przy czym
przy czym
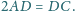 Na odcinku
Na odcinku
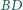 dany jest taki punkt
dany jest taki punkt
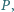 że kąt
że kąt
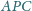 jest prosty.
Udowodnić, że kąty
jest prosty.
Udowodnić, że kąty
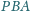 i
i
 są równe.
są równe.
 względem
względem
 Otrzymany
punkt nazwijmy
Otrzymany
punkt nazwijmy
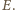 Odcinek
Odcinek
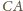 jest środkową trójkąta
jest środkową trójkąta
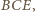 a ponieważ
a ponieważ
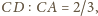 więc
więc
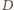 jest
środkiem ciężkości tego trójkąta. Niech
jest
środkiem ciężkości tego trójkąta. Niech
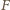 oznacza środek boku
oznacza środek boku
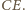 Leży on na przedłużeniu odcinka
Leży on na przedłużeniu odcinka
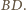 Ponieważ
Ponieważ
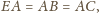 więc kąt
więc kąt
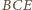 jest prosty, a zatem również kąt
jest prosty, a zatem również kąt
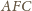 jest prosty. Stąd punkty
jest prosty. Stąd punkty
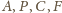 leżą na okręgu o średnicy
leżą na okręgu o średnicy
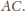 Wobec tego
Wobec tego
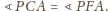 Ale
Ale
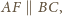 więc
więc
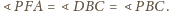
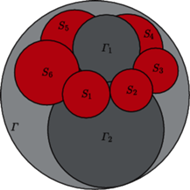
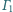 i
i
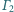 są styczne wewnętrznie do sfery
są styczne wewnętrznie do sfery
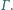 Do każdej z tych trzech sfer styczna jest każda z
Do każdej z tych trzech sfer styczna jest każda z
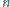 sfer
sfer
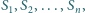 ponadto dla każdego
ponadto dla każdego
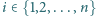 sfera
sfera
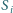 styczna jest do sfery
styczna jest do sfery
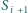 (przy czym
(przy czym
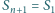 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch sfer
istnieje taki łańcuch sfer
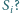 W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
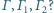 Czy i jak zależy to
od wyboru początkowej sfery
Czy i jak zależy to
od wyboru początkowej sfery
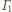 i
i
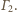 Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
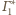 i
i
 Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
 i
i
 jest
środek inwersji.
jest
środek inwersji.
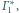
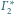
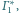
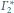
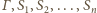 jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
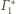 i
i
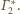 Z równoległości tych płaszczyzn wynika, że wszystkie sfery
Z równoległości tych płaszczyzn wynika, że wszystkie sfery
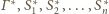 mają średnice równe odległości
mają średnice równe odległości
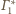 od
od
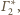 czyli są przystające. Ponadto wszystkie sfery
czyli są przystające. Ponadto wszystkie sfery
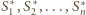 są
styczne do sfery
są
styczne do sfery
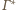 oraz dla każdego
oraz dla każdego
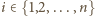 sfera
sfera
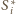 styczna jest do sfery
styczna jest do sfery
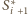 (przy czym
(przy czym
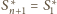 ).
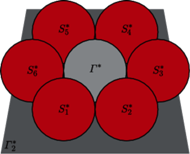
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
).
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
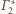 ) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
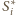 otacza środkową
piłeczkę
otacza środkową
piłeczkę
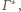 stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
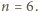
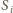 ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
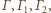 ani też od wyboru sfery
ani też od wyboru sfery
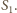 Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
 Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery
Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery
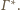
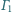 i
i
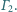 Do
każdego z nich styczny jest każdy z
Do
każdego z nich styczny jest każdy z
 okręgów
okręgów
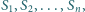 ponadto
dla każdego
ponadto
dla każdego
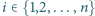 okrąg
okrąg
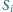 styczny jest do okręgu
styczny jest do okręgu
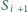 (przy czym
(przy czym
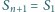 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch
okręgów
istnieje taki łańcuch
okręgów
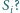 W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
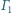 i
i
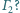 Czy i jak zależy to od wyboru
początkowego okręgu
Czy i jak zależy to od wyboru
początkowego okręgu
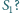
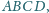 w którym
w którym
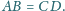 Ponadto
suma pól ścian
Ponadto
suma pól ścian
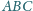 i
i
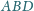 jest równa sumie pól
ścian
jest równa sumie pól
ścian
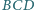 i
i
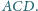 Dowieść, że
Dowieść, że
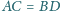 lub
lub
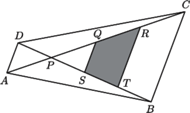
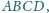 którego przekątne przecinają się
w punkcie
którego przekątne przecinają się
w punkcie
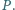 Na przekątnej
Na przekątnej
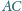 dane są jeszcze punkty
dane są jeszcze punkty
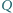 i
i
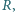 dzielące ją wraz z
dzielące ją wraz z
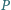 na cztery równe części, tzn.
na cztery równe części, tzn.
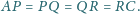 Na przekątnej
Na przekątnej
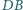 dane są jeszcze punkty
dane są jeszcze punkty
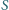 i
i
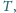 które wraz z
które wraz z
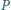 dzielą ją na cztery równe części,
tzn.
dzielą ją na cztery równe części,
tzn.
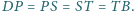 Obliczyć stosunek pól czworokątów
Obliczyć stosunek pól czworokątów
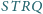 i
i
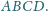
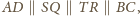 więc
więc
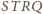 i
i
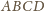 są trapezami o stosunku wysokości
są trapezami o stosunku wysokości
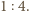
 oznaczmy długość odcinka
oznaczmy długość odcinka
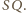 Wówczas
Wówczas
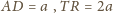 oraz
oraz
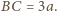 Zatem
Zatem
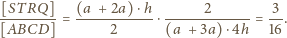
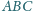 oraz punkt
oraz punkt
 na
boku
na
boku
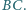 Punkty
Punkty
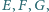 leżące odpowiednio na bokach
leżące odpowiednio na bokach
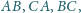 są wyznaczone przez warunki
są wyznaczone przez warunki
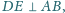
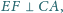
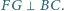 Proste
Proste
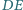 i
i
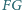 przecinają się
w punkcie
przecinają się
w punkcie
 W jakim stosunku prosta
W jakim stosunku prosta
 dzieli odcinek
dzieli odcinek
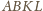 tak, by punkt
tak, by punkt
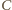 był środkiem
odcinka
był środkiem
odcinka
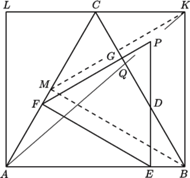
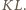 Niech
Niech
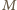 będzie środkiem boku
będzie środkiem boku
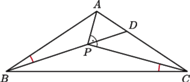
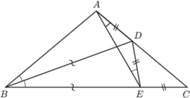
 Każdy
z trójkątów
Każdy
z trójkątów
 ma boki prostopadłe do odpowiednich boków
trójkąta
ma boki prostopadłe do odpowiednich boków
trójkąta
 (rysunek); są to więc trójkąty o bokach odpowiednio
równoległych – zatem jednokładne. Środkiem jednokładności jest punkt
(rysunek); są to więc trójkąty o bokach odpowiednio
równoległych – zatem jednokładne. Środkiem jednokładności jest punkt
 (współliniowy z
(współliniowy z
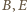 oraz z
oraz z
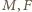 ). Punktowi
). Punktowi
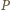 odpowiada w tej jednokładności punkt
odpowiada w tej jednokładności punkt
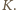 To znaczy, że
prosta
To znaczy, że
prosta
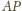 przechodzi przez
przechodzi przez
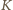 (niezależnie od wyboru
początkowego punktu
(niezależnie od wyboru
początkowego punktu
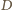 ) i przecina odcinek
) i przecina odcinek
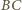 w takim punkcie
w takim punkcie
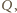 że trójkąty
że trójkąty
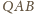 i
i
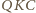 są podobne. Stąd wynik:
są podobne. Stąd wynik:
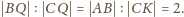
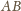 kwadratu to część prostej
kwadratu to część prostej
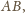 zawarta w kącie
zawarta w kącie
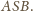
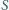 i wpisany w czworokąt wypukły
i wpisany w czworokąt wypukły
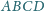 jest styczny do boków
jest styczny do boków
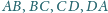 odpowiednio
w punktach
odpowiednio
w punktach
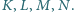 Proste
Proste
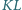 i
i
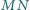 przecinają
się w punkcie
przecinają
się w punkcie
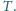 Wykaż, że proste
Wykaż, że proste
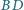 i
i
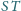 są
prostopadłe.
są
prostopadłe.

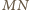 w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
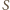 i przez stałe
punkty
i przez stałe
punkty
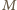 i
i
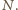 Leży na nim też punkt
Leży na nim też punkt
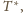 bo
punkt
bo
punkt
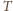 leży na prostej
leży na prostej
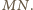 Średnicą tego okręgu jest
Średnicą tego okręgu jest
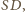 ponieważ kąty
ponieważ kąty
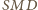 i
i
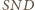 są proste, stąd także
są proste, stąd także
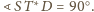
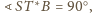 więc
więc
 Z definicji inwersji
punkty
Z definicji inwersji
punkty
 są współliniowe, co kończy dowód.
są współliniowe, co kończy dowód.

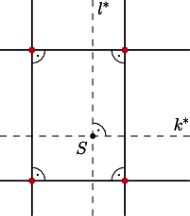
 przy oznaczeniach jak na rysunku. Proste
przy oznaczeniach jak na rysunku. Proste
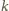 i
i
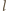 są stałe
przy tej inwersji. Obrazem każdego z okręgów, przechodzącego przez środek
inwersji, jest prosta równoległa odpowiednio do
są stałe
przy tej inwersji. Obrazem każdego z okręgów, przechodzącego przez środek
inwersji, jest prosta równoległa odpowiednio do
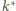 lub
lub
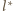 (okrąg
styczny do prostej
(okrąg
styczny do prostej
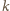 lub
lub
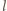 mieści się w półpłaszczyźnie przez
nią wyznaczonej, więc jego obraz też, rysunek obok). Zatem obrazami
kolorowych punktów są wierzchołki prostokąta. Leżą one na okręgu
nieprzechodzącym przez środek inwersji (bo środek ten jest wewnątrz
prostokąta), więc także przed inwersją kolorowe punkty leżą na jednym
okręgu.
mieści się w półpłaszczyźnie przez
nią wyznaczonej, więc jego obraz też, rysunek obok). Zatem obrazami
kolorowych punktów są wierzchołki prostokąta. Leżą one na okręgu
nieprzechodzącym przez środek inwersji (bo środek ten jest wewnątrz
prostokąta), więc także przed inwersją kolorowe punkty leżą na jednym
okręgu.
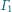 i
i
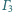 jest styczny zewnętrznie
do każdego z rozłącznych okręgów
jest styczny zewnętrznie
do każdego z rozłącznych okręgów
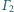 i
i
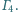 Wykaż, że punkty
styczności leżą na jednym okręgu.
Wykaż, że punkty
styczności leżą na jednym okręgu.
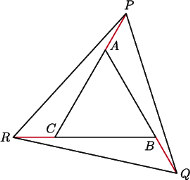
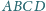 okręgi wpisane w trójkąty
okręgi wpisane w trójkąty
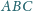 i
i
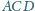 są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
 będących przedłużeniami boków
trójkąta
będących przedłużeniami boków
trójkąta
 obrano odpowiednio punkty
obrano odpowiednio punkty
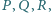 przy czym
przy czym
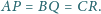 Udowodnić, że jeśli trójkąt
Udowodnić, że jeśli trójkąt
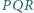 jest
równoboczny, to trójkąt
jest
równoboczny, to trójkąt
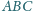 również.
również.
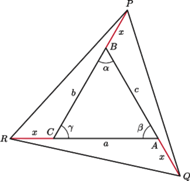
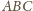 jak na rysunku
i załóżmy, że
jak na rysunku
i załóżmy, że
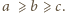
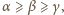 a stąd
a stąd
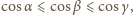 ponieważ
funkcja
ponieważ
funkcja
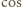 jest malejąca na przedziale
jest malejąca na przedziale
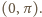 Przyjmijmy,
że
Przyjmijmy,
że
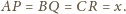 Wówczas z twierdzenia cosinusów
otrzymujemy
Wówczas z twierdzenia cosinusów
otrzymujemy
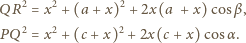
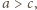 to ponieważ
to ponieważ
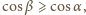 mielibyśmy
mielibyśmy
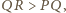 co przeczyłoby założeniu, że trójkąt
co przeczyłoby założeniu, że trójkąt
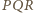 jest
równoboczny. W takim razie
jest
równoboczny. W takim razie
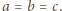
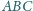 oraz dowolny punkt
oraz dowolny punkt
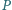 na
jego okręgu wpisanym. Wykaż, że suma
na
jego okręgu wpisanym. Wykaż, że suma
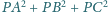 nie zależy od
wyboru punktu
nie zależy od
wyboru punktu
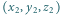
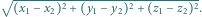
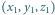
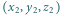
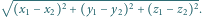
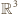 tak, aby
tak, aby
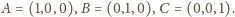 Wtedy równanie płaszczyzny
Wtedy równanie płaszczyzny
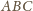 to
to
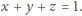
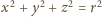 dla takiego
dla takiego
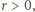 aby okrąg wpisany w trójkąt
aby okrąg wpisany w trójkąt
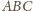 był przekrojem tej sfery
płaszczyzną
był przekrojem tej sfery
płaszczyzną
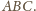
 Wówczas
Wówczas
 z okręgu.
z okręgu.
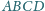 punkty
punkty
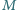 i
i
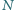 są
odpowiednio środkami boków
są
odpowiednio środkami boków
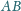 i
i
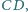 zaś przekątne
przecinają się w punkcie
zaś przekątne
przecinają się w punkcie
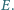 Wykaż, że prosta zawierająca dwusieczną
kąta
Wykaż, że prosta zawierająca dwusieczną
kąta
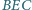 jest prostopadła do prostej
jest prostopadła do prostej
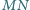 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
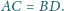
 oraz by
dwusieczna kąta
oraz by
dwusieczna kąta
 była zawarta w dodatniej półosi
była zawarta w dodatniej półosi
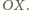
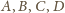 są odpowiednio
są odpowiednio
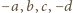 dla pewnych
dla pewnych
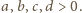
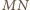 jest prostopadła do osi
jest prostopadła do osi
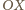 wtedy i tylko wtedy, gdy
pierwsze współrzędne punktów
wtedy i tylko wtedy, gdy
pierwsze współrzędne punktów
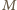 i
i
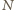 są równe, czyli gdy
są równe, czyli gdy
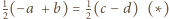 .
.
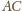 i
i
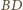 tworzą z poziomą osią ten sam kąt
tworzą z poziomą osią ten sam kąt
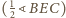 , więc warunek
, więc warunek
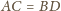 równoważny jest warunkowi,
że rzuty tych odcinków na oś
równoważny jest warunkowi,
że rzuty tych odcinków na oś
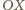 są równe. Każdy z rzutów
zawiera punkt
są równe. Każdy z rzutów
zawiera punkt
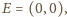 zatem są one równe wtedy i tylko wtedy, gdy
zatem są one równe wtedy i tylko wtedy, gdy
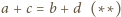 .
.
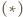 i
i
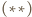 są równoważne, co kończy dowód.
są równoważne, co kończy dowód.
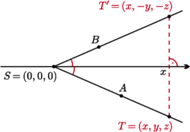
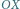




 czworościanu był w punkcie
czworościanu był w punkcie
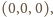 a prostopadłe
dwusieczne kątów płaskich
a prostopadłe
dwusieczne kątów płaskich
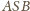 i
i
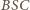 były zawarte odpowiednio
w dodatnich półosiach
były zawarte odpowiednio
w dodatnich półosiach
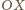 i
i
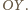
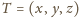 z półprostej
z półprostej
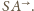 Jego
obrazem w symetrii względem osi
Jego
obrazem w symetrii względem osi
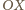 jest punkt
jest punkt
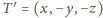 na
półprostej
na
półprostej
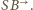
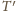 w symetrii względem osi
w symetrii względem osi
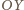 jest
punkt
jest
punkt
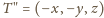 na półprostej
na półprostej
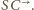 Punkty
Punkty
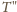 i
i
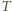 są więc symetryczne względem osi
są więc symetryczne względem osi
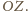 Zatem,
z dowolności wyboru
Zatem,
z dowolności wyboru
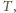 całe półproste
całe półproste
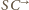 i
i
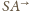 są
symetryczne względem
są
symetryczne względem
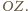 Stąd dwusieczna kąta
Stąd dwusieczna kąta
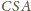 zawarta
jest w osi
zawarta
jest w osi
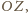 co kończy dowód.
co kończy dowód.
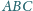 kąt przy wierzchołku
kąt przy wierzchołku
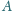 ma
miarę
ma
miarę
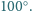 Dwusieczna kąta przy wierzchołku
Dwusieczna kąta przy wierzchołku
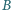 przecina bok
przecina bok
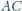 w punkcie
w punkcie
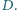 Udowodnić, że
Udowodnić, że
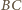 taki punkt
taki punkt
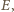 że
że
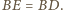
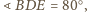 a skoro
a skoro
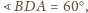 to
to
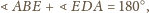
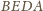 można opisać okrąg. Wobec tego
można opisać okrąg. Wobec tego
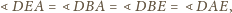
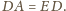 Z drugiej strony,
Z drugiej strony,
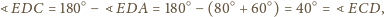
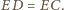 Zatem
Zatem
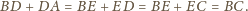
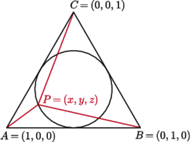
 oraz dowolny punkt
oraz dowolny punkt
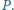 Niech
Niech
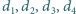 będą
odległościami punktu
będą
odległościami punktu
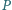 od wierzchołków czworościanu. Wykazać,
że
od wierzchołków czworościanu. Wykazać,
że


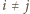 mamy wówczas
mamy wówczas
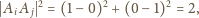
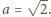 Nie ogranicza to
ogólności rozumowania, bo równość podana do udowodnienia ma po obu
stronach wyrażenia jednorodne stopnia 4.
Nie ogranicza to
ogólności rozumowania, bo równość podana do udowodnienia ma po obu
stronach wyrażenia jednorodne stopnia 4.
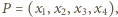 leżący w tej samej
przestrzeni trójwymiarowej, co punkty
leżący w tej samej
przestrzeni trójwymiarowej, co punkty
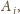 czyli taki, że
czyli taki, że
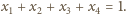 Przyjmijmy, że leży on w odległości
Przyjmijmy, że leży on w odległości
 od
początku układu współrzędnych:
od
początku układu współrzędnych:
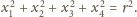 Obliczamy:
Obliczamy:
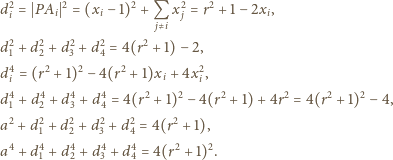
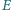 i
i
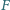 leżą odpowiednio na bokach
leżą odpowiednio na bokach
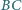 i
i
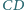 kwadratu
kwadratu
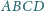 o boku 1, przy czym
o boku 1, przy czym
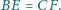 Udowodnij, że
Udowodnij, że
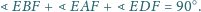
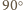 wokół środka. Obrazem trójkąta
wokół środka. Obrazem trójkąta
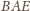 jest trójkąt
jest trójkąt
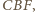 zatem
zatem
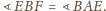 Analogicznie
Analogicznie
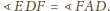 Stąd
Stąd
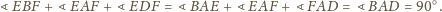
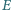 i
i
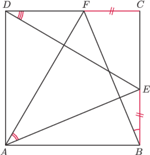
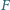 leżą odpowiednio na bokach
leżą odpowiednio na bokach
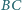 i
i
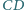 kwadratu
kwadratu
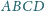 o boku 1, przy czym
o boku 1, przy czym
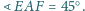 Wykaż, że
Wykaż, że
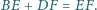
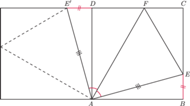
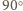 wokół wierzchołka
wokół wierzchołka
 niech
niech
 będzie obrazem punktu
będzie obrazem punktu
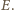 Wtedy
Wtedy
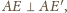 zatem
zatem
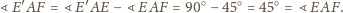
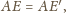 więc
więc
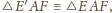 bo trójkąty te mają
dodatkowo wspólny bok
bo trójkąty te mają
dodatkowo wspólny bok
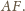 Stąd
Stąd