Zadanie ZM-1571
o zadaniu...
- Publikacja w Delcie: lipiec 2018
- Publikacja elektroniczna: 30 czerwca 2018
Wewnątrz trójkąta równobocznego 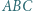 wyznacz zbiór takich punktów
wyznacz zbiór takich punktów  że miary kątów
że miary kątów 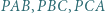 tworzą w tej właśnie kolejności ciąg arytmetyczny.
tworzą w tej właśnie kolejności ciąg arytmetyczny.
Wewnątrz trójkąta równobocznego  wyznacz zbiór takich punktów
wyznacz zbiór takich punktów 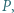 że miary kątów
że miary kątów 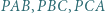 tworzą w tej właśnie kolejności ciąg arytmetyczny.
tworzą w tej właśnie kolejności ciąg arytmetyczny.
Czy istnieje taki wielościan wypukły 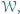 który można rozciąć płaszczyzną na dwa wielościany podobne do
który można rozciąć płaszczyzną na dwa wielościany podobne do 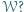
Trójkąt 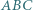 (nie prostokątny) jest wpisany w okrąg o średnicy
(nie prostokątny) jest wpisany w okrąg o średnicy 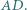 Punkt
Punkt 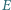 jest symetryczny do
jest symetryczny do 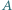 względem środka boku
względem środka boku 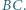 Dowieść, że okręgi opisane na trójkątach
Dowieść, że okręgi opisane na trójkątach 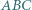 i
i 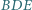 mają równe promienie.
mają równe promienie.
Udowodnij, że punkt 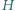 jest ortocentrum trójkąta
jest ortocentrum trójkąta 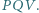
Niech proste 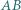 i
i 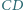 przecinają się w punkcie
przecinają się w punkcie 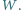 Wykaż, że
Wykaż, że 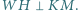
Okrąg wpisany w trójkąt 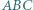 jest styczny do boków
jest styczny do boków 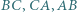 odpowiednio w punktach
odpowiednio w punktach 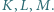 Udowodnij, że proste przechodzące przez środki odcinków
Udowodnij, że proste przechodzące przez środki odcinków 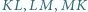 i prostopadłe odpowiednio do boków
i prostopadłe odpowiednio do boków 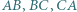 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Niech 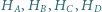 będą odpowiednio ortocentrami trójkątów
będą odpowiednio ortocentrami trójkątów 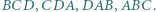 Wykaż, że odcinki
Wykaż, że odcinki 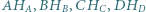 mają wspólny punkt.
mają wspólny punkt.
Niech 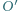 i
i 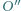 oznaczają odbicia symetryczne punktu
oznaczają odbicia symetryczne punktu 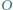 względem prostych
względem prostych 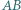 i
i 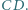 Udowodnij, że punkt
Udowodnij, że punkt 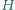 leży na prostej
leży na prostej 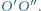
Udowodnij, że płaszczyzny przechodzące przez środki krawędzi czworościanu i prostopadłe do przeciwległych krawędzi mają wspólny punkt (punkt Monge'a).
Wykaż, że w każdym trójkącie ortocentrum 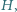 środek ciężkości
środek ciężkości 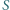 i środek okręgu opisanego
i środek okręgu opisanego 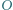 leżą na jednej prostej (prostej Eulera), w tej kolejności i
leżą na jednej prostej (prostej Eulera), w tej kolejności i 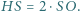
Wykaż, że w dowolnym trójkącie proste równoległe do dwusiecznych poprowadzone przez środki przeciwległych boków przecinają się w jednym punkcie.
Wyznaczyć iloczyn długości wszystkich boków i przekątnych 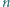 -kąta foremnego wpisanego w okrąg o promieniu 1.
-kąta foremnego wpisanego w okrąg o promieniu 1.
Pierwsza ćwiartka płaszczyzny z kartezjańskim układem współrzędnych jest podzielona prostymi o równaniach 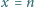 oraz
oraz 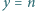 dla
dla 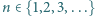 na kwadraty jednostkowe, zwane dalej polami. Czy można wyróżnić niektóre pola w taki sposób, że:
na kwadraty jednostkowe, zwane dalej polami. Czy można wyróżnić niektóre pola w taki sposób, że:
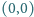 zawiera więcej pól wyróżnionych niż niewyróżnionych;
zawiera więcej pól wyróżnionych niż niewyróżnionych;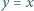 przecina wnętrze tylko skończenie wielu wyróżnionych pól?
przecina wnętrze tylko skończenie wielu wyróżnionych pól?Zadanie 758 zaproponował pan Witold Bednarek z Łodzi.
Trzy okręgi o promieniach 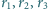 są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu
są parami styczne zewnętrznie oraz są styczne wewnętrznie do okręgu o promieniu 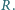 Wykazać, że
Wykazać, że

Wewnątrz sześciokąta wypukłego 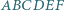 leży taki punkt
leży taki punkt 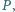 że spełnione są równości
że spełnione są równości 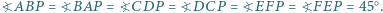 Udowodnij, że suma długości odcinków
Udowodnij, że suma długości odcinków 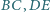 i
i 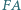 jest nie mniejsza od każdego z odcinków
jest nie mniejsza od każdego z odcinków 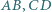 i
i 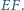
Dany jest pięciokąt wypukły 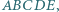 w którym
w którym 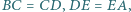
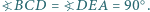 Udowodnij, że z odcinków o długościach
Udowodnij, że z odcinków o długościach 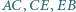 można zbudować trójkąt. Wyznacz miary jego kątów, znając miarę
można zbudować trójkąt. Wyznacz miary jego kątów, znając miarę  kąta
kąta 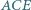 i miarę
i miarę 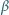 kąta
kąta 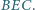
W sześciokącie wypukłym 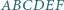 wszystkie boki są równej długości oraz
wszystkie boki są równej długości oraz 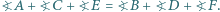 Udowodnij, że przekątne
Udowodnij, że przekątne 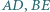 i
i 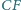 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Mamy do dyspozycji cztery wycięte z papieru przystające trójkąty prostokątne. Możemy wielokrotnie wykonywać operację polegającą na wybraniu jednego z kawałków i rozcięciu go wzdłuż wysokości, poprowadzonej z wierzchołka kąta prostego, na dwa mniejsze trójkąty prostokątne. Wykazać, że po wykonaniu skończonej liczby cięć zawsze co najmniej dwa kawałki będą przystające.
W czworokącie wypukłym 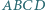 punkty
punkty 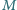 i
i 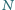 są odpowiednio środkami boków
są odpowiednio środkami boków 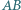 i
i 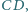 zaś przekątne przecinają się w punkcie
zaś przekątne przecinają się w punkcie 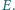 Wykazać, że prosta zawierająca dwusieczną kąta
Wykazać, że prosta zawierająca dwusieczną kąta 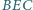 jest prostopadła do prostej
jest prostopadła do prostej 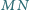 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 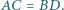
Dany jest czworokąt 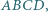 w którym
w którym 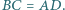 Na bokach
Na bokach 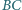 i
i 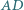 zbudowano na zewnątrz takie trójkąty
zbudowano na zewnątrz takie trójkąty 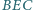 i
i 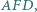 że
że 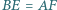 oraz
oraz 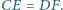 Udowodnić, że środki odcinków
Udowodnić, że środki odcinków 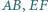 i
i 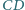 leżą na jednej prostej.
leżą na jednej prostej.
Na płaszczyźnie dane są kwadraty 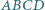 oraz
oraz 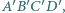 przeciwnie zorientowane o bokach odpowiednio długości
przeciwnie zorientowane o bokach odpowiednio długości 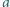 i
i 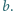 Punkty
Punkty 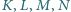 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 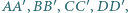 przy czym
przy czym

Dowieść, że punkty 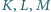 i
i 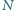 leżą na jednej prostej.
leżą na jednej prostej.
Częścią wspólną dwóch jednakowych kwadratów jest ośmiokąt. Boki jednego z kwadratów zostały narysowane na czerwono, drugiego zaś na niebiesko. Udowodnić, że suma długości czerwonych boków ośmiokąta jest równa sumie długości jego niebieskich boków.
Płaszczyzna przecina krawędzie boczne graniastosłupa prostego o podstawie równoległoboku, tworząc w przekroju czworokąt wypukły 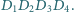 Niech
Niech 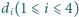 będzie odległością punktu
będzie odległością punktu 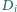 od płaszczyzny ustalonej podstawy graniastosłupa. Udowodnić, że
od płaszczyzny ustalonej podstawy graniastosłupa. Udowodnić, że

Płaszczyzna przecina krawędzie boczne graniastosłupa prawidłowego sześciokątnego, tworząc w przekroju sześciokąt wypukły 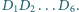 Niech
Niech 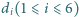 będzie odległością punktu
będzie odległością punktu 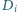 od płaszczyzny ustalonej podstawy graniastosłupa. Dowieść, że
od płaszczyzny ustalonej podstawy graniastosłupa. Dowieść, że
