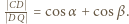Kochajcie trygonometrię, dziewczęta»Zadanie 8
o zadaniu...
- Zadanie pochodzi z artykułu Kochajcie trygonometrię, dziewczęta
- Publikacja w Delcie: luty 2020
- Publikacja elektroniczna: 1 lutego 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)
W trókjącie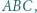 
wpisanym w okrąg o środku 
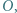kąt przy wierzchołku 
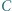jest rozwarty oraz zachodzi równość 
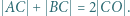Odcinki 
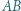i 
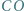przecinają się w punkcie 
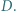Dwusieczne kątów 
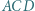i 
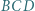przecinają odcinek 
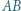w punktach odpowiednio 
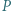i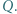 
Dowieść, że punkt 
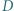jest środkiem odcinka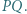 
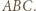Wskazówka
Przyjmijmy standardowe oznaczenia dla trójkąta 
Z twierdzenia o dwusiecznej zastosowanego dla trójkąta 
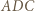otrzymujemy 
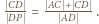Miary kątów trójkąta 
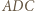wynoszą odpowiednio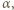 
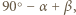
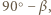więc z twierdzenia sinusów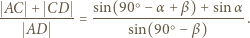
 |
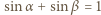Po uproszczeniu i zastosowaniu równości 
(treść zadania + twierdzenie sinusów), otrzymamy
 |
Analogicznie postępując, dojdziemy do równości 