Klub 44M - zadania V 2020»Zadanie 801
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania V 2020
- Publikacja w Delcie: maj 2020
- Publikacja elektroniczna: 30 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (479 KB)
Na przyprostokątnej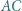 
trójkąta prostokątnego 
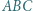został dowolnie wybrany punkt 
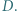Symetralna odcinka 
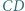przecina przeciwprostokątną 
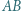w punkcie 
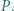Punkt 
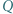jest symetryczny do 
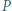względem środka 
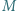odcinka 
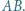Punkt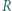 
jest rzutem prostokątnym punktu 
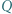na prostą 
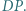Udowodnić, że 
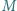leży na dwusiecznej kąta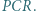 
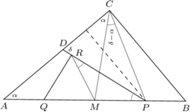
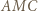i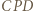 
są równoramienne. Przyjmijmy oznaczenia: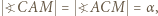 
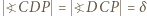; zatem 
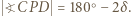Środek odcinka 
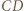leży bliżej punktu 
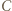niż punktu 
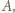wobec czego punkt 
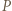leży między 
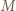i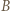 
; w takim razie 
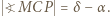Rachunek kątów w trójkącie 
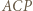pokazuje, że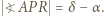 
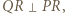trójkąt 
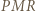jest równoramienny, więc 
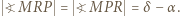Uzyskujemy równość 
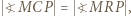z której wynika, że czworokąt 
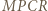ma okrąg opisany. Skoro 
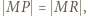punkt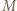 
jest środkiem łuku 
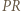tego okręgu; a to znaczy, że półprosta 
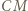połowi kąt 
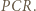To teza zadania.