Klub 44M - zadania XI 2019»Zadanie 790
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania XI 2019
- Publikacja w Delcie: listopad 2019
- Publikacja elektroniczna: 31 października 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (376 KB)
-
Zadanie 790 zaproponował pan Mikołaj Pater.
Na bokach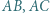 
trójkąta ostrokątnego 
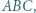po jego zewnętrznej stronie, zbudowano trójkąty prostokątne równoramienne 
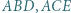z kątami prostymi przy wierzchołkach 
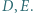Odcinki 
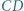i 
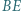przecinają się w punkcie 
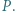Punkty 
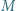i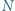 
są środkami odcinków 
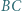i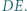 
Udowodnić, że każda z prostych 
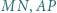jest prostopadła do prostej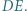 
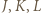będą rzutami prostokątnymi punktów 
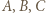na prostą 
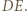Trójkąt prostokątny 
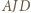jest przystający do trójkąta 
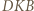; analogicznie, trójkąt 
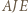przystaje do 
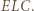Zatem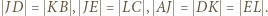 
Z ostatniej równości wynika, że środek 
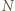odcinka 
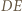jest też środkiem odcinka 
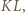i wobec tego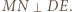 
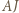przecina odcink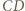i 
i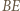 
w punktach, które nazwiemy odpowiednio 
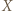i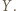 
Z proporcji
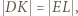zatem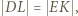 
i w takim razie 
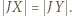To oznacza, że 
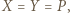a prosta 
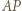to prosta 
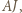prostopadła (z definicji) do 