Składanie inwersji z symetrią»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Składanie inwersji z symetrią
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (390 KB)
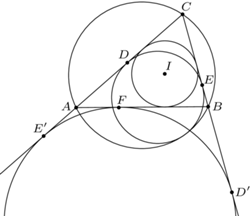
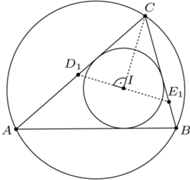
Okrąg o środku 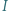 jest wpisany w trójkąt
jest wpisany w trójkąt 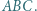 Okrąg
Okrąg 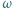 styczny do okręgu opisanego na trójkącie
styczny do okręgu opisanego na trójkącie 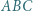 jest styczny do odcinków
jest styczny do odcinków 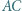 i
i 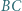 odpowiednio w punktach
odpowiednio w punktach 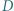 i
i 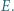 Wykazać, że punkt
Wykazać, że punkt 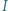 leży na odcinku
leży na odcinku 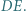

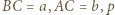 to połowa obwodu trójkąta
to połowa obwodu trójkąta 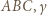 to miara kąta
to miara kąta 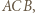 zaś
zaś  to promień okręgu wpisanego w trójkąt
to promień okręgu wpisanego w trójkąt 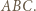 Inwersja o środku
Inwersja o środku 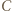 i promieniu
i promieniu 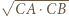 złożona z symetrią względem dwusiecznej kąta
złożona z symetrią względem dwusiecznej kąta 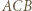 przeprowadza okrąg
przeprowadza okrąg 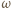 na okrąg dopisany do trójkąta
na okrąg dopisany do trójkąta 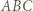 styczny do boku
styczny do boku 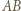 w punkcie
w punkcie 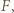 a punkty
a punkty 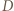 i
i 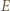 odpowiednio na punkty
odpowiednio na punkty 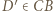 i
i 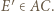 Ponieważ
Ponieważ 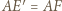 i
i 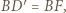 to
to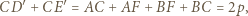
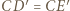 prowadzi do wniosku, że
prowadzi do wniosku, że 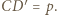 Z drugiej strony z definicji inwersji mamy
Z drugiej strony z definicji inwersji mamy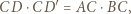
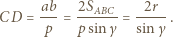
 i prostopadła do prostej
i prostopadła do prostej 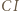 przecina boki
przecina boki 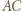 i
i 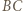 odpowiednio w punktach
odpowiednio w punktach 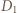 i
i 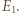 Skoro
Skoro 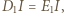 to odległość punktu
to odległość punktu 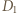 od prostej
od prostej 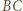 jest równa
jest równa 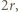 skąd wniosek, że
skąd wniosek, że 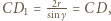 czyli
czyli 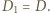 Analogicznie uzasadnimy, że
Analogicznie uzasadnimy, że 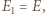 więc punkt
więc punkt 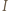 leży na odcinku
leży na odcinku