Zadanie

Narzędzia
Obiekty: Wielokąty
Słowa kluczowe
Kategoria: Planimetria

Nic nie może przecież wiecznie trwać»Zadanie 6

o zadaniu...

Zadanie pochodzi z artykułu Nic nie może przecież wiecznie trwać
Publikacja w Delcie: sierpień 2020
Publikacja elektroniczna: 1 sierpnia 2020
Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)

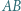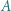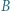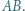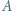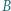Mamy dany wielokąt wklęsły. Ruch polega na wyborze przekątnej $AB$ leżącej na zewnątrz tego wielokąta, przy czym cały wielokąt poza punktami $|A$ i $B |$ musi leżeć po jednej stronie prostej $AB.$ Następnie jedną z łamanych, na które punkty $|A$ i $B |$ dzielą brzeg wielokąta, odbijamy środkowosymetrycznie względem środka odcinka 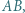$AB,$ otrzymując nowy wielokąt. Dowieść, że po pewnej, skończonej liczbie takich operacji, otrzymamy wielokąt wypukły.

Wskazówka

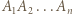Jest jasne, że pole wielokąta wzrasta po każdym ruchu. Wystarczy wykazać, że przyjmuje ono tylko skończenie wiele wartości. W tym celu dla wielokąta $|A$ rozważmy wektory 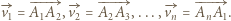$−v =−− A−− ,−v = −−A−− ,...,−v = −−−A− . 1 2 n$ Wykonanie ruchu zmienia jedynie kolejność wektorów 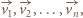$− − − |v1,v2,...,vn,$ a ta jednoznacznie określa pole wielokąta.