Jeżeli można dokonać podziału, to rozważając wszystkie równoległoboki mające jeden z boków równoległy do ustalonego boku wielokąta, dojdziemy do wniosku, że ten wielokąt ma bok równoległy do ustalonego, o tej samej długości. Jest tak dla każdego boku, a wielokąt jest wypukły, więc ma on środek symetrii.

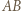W drugą stronę, niech będzie jednym z boków wielokąta środkowosymetrycznego 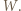Przez 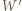oznaczmy wielokąt 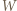przesunięty o wektor 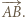Wówczas wielokąt 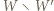łatwo rozciąć na równoległoboki, a wielokąt 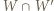ma środek symetrii i o dwa boki mniej niż wielokąt