Kąty dwuścienne»Zadanie 4
o zadaniu...
- Zadanie olimpijskie: Olimpiada Matematyczna 45-I-12
- Zadanie pochodzi z artykułu Kąty dwuścienne
- Publikacja w Delcie: październik 2011
- Publikacja elektroniczna: 02-10-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (64 KB)
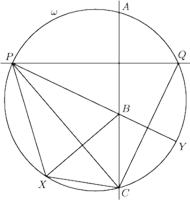
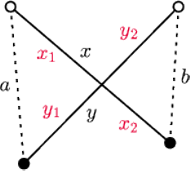
Wykazać, że sumy przeciwległych kątów dwuściennych czworościanu są równe wtedy i tylko wtedy, gdy sumy długości przeciwległych krawędzi są równe.
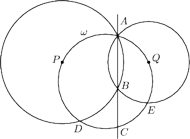
 i
i
 przecinają się w punktach
przecinają się w punktach
 i
i
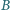 ; promienie
; promienie
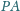 i
i
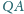 nie są prostopadłe. Okrąg opisany na
trójkącie
nie są prostopadłe. Okrąg opisany na
trójkącie
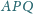 przecina te dwa okręgi w punktach
przecina te dwa okręgi w punktach
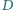 i
i
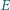 (różnych od
(różnych od
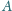 ) oraz przecina prostą
) oraz przecina prostą
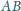 w punkcie
w punkcie
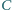 (różnym od
(różnym od
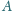 ). Dowieść, że okrąg opisany na trójkącie
). Dowieść, że okrąg opisany na trójkącie
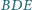 ma środek w punkcie
ma środek w punkcie
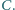
 opisany na trójkącie
opisany na trójkącie
 nie jest styczny do żadnego
z dwóch danych okręgów (bo je przecina w punktach różnych od
nie jest styczny do żadnego
z dwóch danych okręgów (bo je przecina w punktach różnych od
 ).
Zatem żaden z odcinków
).
Zatem żaden z odcinków
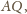
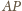 nie jest jego średnicą;
w takim razie żaden z kątów
nie jest jego średnicą;
w takim razie żaden z kątów
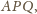
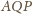 nie jest prosty. Stąd
wniosek, że żaden z punktów
nie jest prosty. Stąd
wniosek, że żaden z punktów
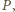
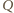 nie leży na prostej
nie leży na prostej
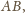 wobec czego prosta
wobec czego prosta
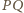 nie przechodzi przez punkt
nie przechodzi przez punkt
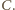
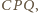 wpisany w okrąg
wpisany w okrąg
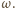 Wysokość poprowadzona z wierzchołka
Wysokość poprowadzona z wierzchołka
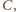 lub jej przedłużenie,
przecina okrąg
lub jej przedłużenie,
przecina okrąg
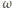 ponownie w punkcie
ponownie w punkcie
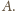 Ortocentrum trójkąta
Ortocentrum trójkąta
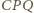 leży w punkcie symetrycznym do
leży w punkcie symetrycznym do
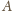 względem prostej
względem prostej
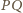 – czyli w punkcie
– czyli w punkcie
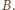
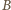 względem boków
względem boków
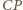 i
i
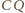 także leżą na okręgu
także leżą na okręgu
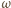 ; oznaczmy je odpowiednio przez
; oznaczmy je odpowiednio przez
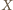 i
i
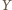 (żaden z nich nie pokrywa się z
(żaden z nich nie pokrywa się z
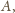 bo punkt
bo punkt
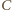 nie leży na prostej
nie leży na prostej
 ).
).
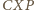 jest symetryczny do
jest symetryczny do
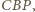 więc
więc
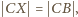
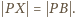 Ostatnia równość mówi, że
Ostatnia równość mówi, że
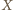 jest punktem okręgu o środku
jest punktem okręgu o środku
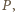 przechodzącego przez
przechodzącego przez
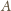 i
i
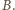 Skoro zaś leży na okręgu
Skoro zaś leży na okręgu
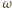 i nie pokrywa się z
i nie pokrywa się z
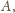 musi się pokrywać z
musi się pokrywać z
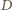 lub
lub
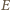 ; ustalmy oznaczenia (
; ustalmy oznaczenia (
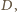
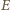 ) tak, że
) tak, że
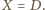 Analogicznie stwierdzamy,
że
Analogicznie stwierdzamy,
że
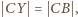
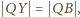
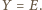 Tak więc
Tak więc
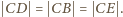 To znaczy, że punkty
To znaczy, że punkty
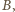
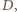
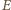 leżą
na okręgu o środku
leżą
na okręgu o środku
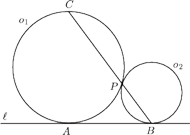
 i
i
 , styczne zewnętrznie w punkcie
, styczne zewnętrznie w punkcie
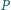 , są
styczne do prostej
, są
styczne do prostej
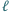 w punktach
w punktach
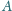 i
i
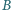 odpowiednio.
Prosta
odpowiednio.
Prosta
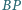 przecina okrąg
przecina okrąg
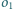 w punkcie
w punkcie
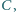 różnym
od
różnym
od
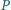 . Udowodnić, że proste
. Udowodnić, że proste
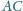 i
i
 są prostopadłe.
są prostopadłe.
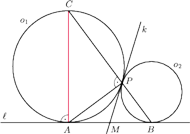
 okręgów
okręgów
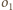 i
i
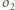 przechodzącą przez punkt
przechodzącą przez punkt
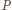 . Przecina ona prostą
. Przecina ona prostą
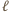 w punkcie
w punkcie
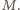 Ponieważ
Ponieważ
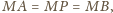 więc trójkąt
więc trójkąt
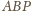 jest
prostokątny. Wobec tego
jest
prostokątny. Wobec tego
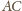 jest średnicą okręgu
jest średnicą okręgu
 jako cięciwa,
na której oparty jest kąt prosty
jako cięciwa,
na której oparty jest kąt prosty
 a średnica okręgu jest
prostopadła do stycznej w swoim końcu.
a średnica okręgu jest
prostopadła do stycznej w swoim końcu.
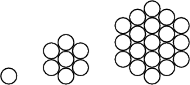
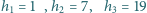
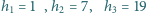
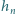 oraz wzór na sumę
oraz wzór na sumę
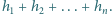

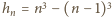 oraz że
oraz że
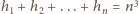 ?
?

 układamy romby o boku długości 1 i kącie
układamy romby o boku długości 1 i kącie
 Każdy
z rombów ma krótszą przekątną równoległą do któregoś z boków
sześciokąta, można zatem wyróżnić trzy orientacje rombów. Wykaż, że
przy każdym wypełnieniu pudełka zawsze jest tyle samo rombów każdej
z trzech orientacji.
Każdy
z rombów ma krótszą przekątną równoległą do któregoś z boków
sześciokąta, można zatem wyróżnić trzy orientacje rombów. Wykaż, że
przy każdym wypełnieniu pudełka zawsze jest tyle samo rombów każdej
z trzech orientacji.

 oraz punkt
oraz punkt
 w jego wnętrzu. Punkty
w jego wnętrzu. Punkty
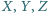 są obrazami punktu
są obrazami punktu
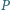 w symetriach odpowiednio
względem środków odcinków
w symetriach odpowiednio
względem środków odcinków
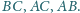 Wykaż, że proste
Wykaż, że proste
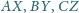 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
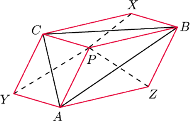
 tworzą równoległobok, bo środek boku
tworzą równoległobok, bo środek boku
 jest zarazem środkiem odcinka
jest zarazem środkiem odcinka
 Podobnie
Podobnie
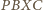 i
i
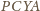 są równoległobokami. Kolorowa część rysunku, widziana
przestrzennie, to pewien równoległościan. Odcinki
są równoległobokami. Kolorowa część rysunku, widziana
przestrzennie, to pewien równoległościan. Odcinki
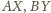 i
i
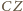 przecinają się w jednym punkcie jako jego przekątne.
przecinają się w jednym punkcie jako jego przekątne.
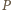 na zewnątrz trójkąta
na zewnątrz trójkąta
 rozwiązanie jest
analogiczne.
rozwiązanie jest
analogiczne.
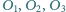 wszystkie mają promień
wszystkie mają promień
 i przecinają się
odpowiednio:
i przecinają się
odpowiednio:
 z
z
 w punktach
w punktach
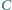 i
i
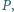
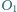 i
i
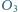 w punktach
w punktach
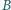 i
i
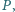
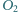 i
i
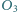 w punktach
w punktach
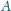 i
i
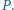 Udowodnij, że okrąg opisany na trójkącie
Udowodnij, że okrąg opisany na trójkącie
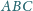 również ma promień
również ma promień
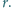
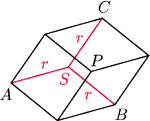
 Wszystkie są równe, więc otrzymane trzy czworokąty są
rombami (
Wszystkie są równe, więc otrzymane trzy czworokąty są
rombami (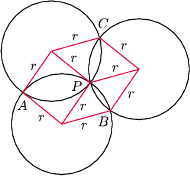
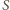 (
(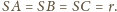 Punkt
Punkt
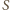 jest więc środkiem
okręgu o promieniu
jest więc środkiem
okręgu o promieniu
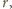 opisanego na trójkącie
opisanego na trójkącie
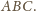 Dla
punktu
Dla
punktu
 na zewnątrz trójkąta
na zewnątrz trójkąta
 rozwiązanie jest
analogiczne.
rozwiązanie jest
analogiczne.
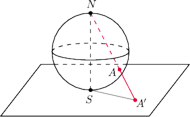
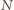 tej sfery, przeciwległym do punktu
tej sfery, przeciwległym do punktu
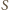 styczności ze stołem,
zapalamy żarówkę. Zaznaczamy na powierzchni sfery dowolny punkt
styczności ze stołem,
zapalamy żarówkę. Zaznaczamy na powierzchni sfery dowolny punkt
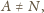 a na stole jego cień
a na stole jego cień
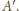 Taki
Taki
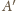 nazywamy
rzutem stereograficznym punktu
nazywamy
rzutem stereograficznym punktu
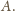 Rzut ten działa na punktach
rozważanej sfery tak, jak inwersja o środku
Rzut ten działa na punktach
rozważanej sfery tak, jak inwersja o środku
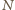 i promieniu
i promieniu
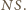
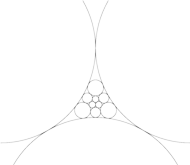
 przeprowadza na okręgi oraz zachowuje
styczność.
przeprowadza na okręgi oraz zachowuje
styczność.
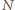 będzie dowolnym z punktów sfery, leżących na zewnątrz
wszystkich okręgów. Rzut stereograficzny z
będzie dowolnym z punktów sfery, leżących na zewnątrz
wszystkich okręgów. Rzut stereograficzny z
 przeprowadza naszą
przestrzenną konfigurację na szukaną płaską konfigurację okręgów (rysunek
obok).
przeprowadza naszą
przestrzenną konfigurację na szukaną płaską konfigurację okręgów (rysunek
obok).
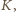 współśrodkowe z nim, o promieniu 97 mm. Czy jest możliwe, aby
kolorowe pasy pokryły całe koło
współśrodkowe z nim, o promieniu 97 mm. Czy jest możliwe, aby
kolorowe pasy pokryły całe koło
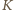 ? Jeśli nie, to dowolny z niepokrytych
punktów „nadaje się” jako środek guzika. Jak oszacować pole powierzchni
koła przykrytej przez pasy?
? Jeśli nie, to dowolny z niepokrytych
punktów „nadaje się” jako środek guzika. Jak oszacować pole powierzchni
koła przykrytej przez pasy?

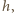
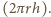
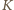 z pasami
jako na rzut (widok z góry) pewnej kuli, wtedy pasy te odpowiadają
plastrom. Wobec tego łączne pole 32 pasów na powierzchni kuli równe
jest co najwyżej
z pasami
jako na rzut (widok z góry) pewnej kuli, wtedy pasy te odpowiadają
plastrom. Wobec tego łączne pole 32 pasów na powierzchni kuli równe
jest co najwyżej
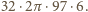 Tymczasem powierzchnia kuli
o promieniu 97 mm równa jest
Tymczasem powierzchnia kuli
o promieniu 97 mm równa jest
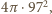 czyli więcej. Zatem
pasy nie pokrywają całej kuli, więc ich rzuty nie pokrywają całego koła
czyli więcej. Zatem
pasy nie pokrywają całej kuli, więc ich rzuty nie pokrywają całego koła
 i w dowolnym z niepokrytych punktów możemy umieścić
środek guzika o promieniu 3 mm.
i w dowolnym z niepokrytych punktów możemy umieścić
środek guzika o promieniu 3 mm.
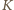 o promieniu 97 mm. Dowiedliśmy, że żadne
inne ich ułożenie też nie wystarcza. W 1932 r. A. Tarski postawił
ogólniejszy
o promieniu 97 mm. Dowiedliśmy, że żadne
inne ich ułożenie też nie wystarcza. W 1932 r. A. Tarski postawił
ogólniejszy
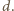
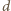
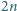 różnych punktów:
różnych punktów:
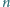 białych
oraz
białych
oraz
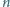 czarnych. Żadne trzy nie leżą na jednej prostej. Udowodnić,
że można tak narysować
czarnych. Żadne trzy nie leżą na jednej prostej. Udowodnić,
że można tak narysować
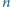 odcinków o końcach w danych
odcinków o końcach w danych
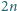 punktach, aby końce były różnokolorowe i aby narysowane odcinki
nie przecinały się.
punktach, aby końce były różnokolorowe i aby narysowane odcinki
nie przecinały się.
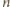 odcinków o różnokolorowych końcach możemy
skonstruować na skończenie wiele sposobów (dokładnie
odcinków o różnokolorowych końcach możemy
skonstruować na skończenie wiele sposobów (dokładnie
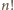 ).
Narysujmy go tak, aby suma długości narysowanych odcinków była możliwie
najmniejsza. Wtedy te odcinki są parami rozłączne, bo w przeciwnym przypadku
parę
).
Narysujmy go tak, aby suma długości narysowanych odcinków była możliwie
najmniejsza. Wtedy te odcinki są parami rozłączne, bo w przeciwnym przypadku
parę
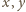 przecinających się odcinków (
przecinających się odcinków (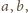 zmniejszając jednocześnie
sumę długości wszystkich odcinków. Wynika to łatwo z nierówności
trójkąta:
zmniejszając jednocześnie
sumę długości wszystkich odcinków. Wynika to łatwo z nierówności
trójkąta:
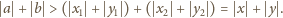
 jest styczny do boków
jest styczny do boków
 odpowiednio w punktach
odpowiednio w punktach
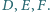 Prowadzimy trzy
proste: przez środki odcinków
Prowadzimy trzy
proste: przez środki odcinków
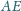 i
i
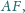 przez środki
odcinków
przez środki
odcinków
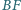 i
i
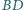 oraz przez środki odcinków
oraz przez środki odcinków
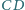 i
i
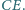 Wykazać, że środek okręgu opisanego na trójkącie wyznaczonym
przez te trzy proste pokrywa się ze środkiem okręgu opisanego na trójkącie
Wykazać, że środek okręgu opisanego na trójkącie wyznaczonym
przez te trzy proste pokrywa się ze środkiem okręgu opisanego na trójkącie
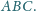
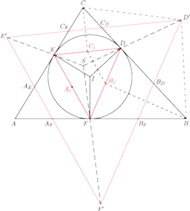
 będą środkami odcinków
będą środkami odcinków
 Z twierdzenia Talesa wynika, że
Z twierdzenia Talesa wynika, że
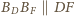 i
i
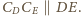 Przez
Przez
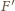 oznaczamy punkt wspólny prostych
oznaczamy punkt wspólny prostych
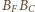 i
i
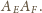 Analogicznie definiujemy punkty
Analogicznie definiujemy punkty
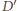 i
i
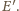 Boki
trójkątów
Boki
trójkątów
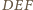 i
i
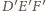 są odpowiednio równoległe, więc
punkt
są odpowiednio równoległe, więc
punkt
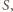 w którym przecinają się proste
w którym przecinają się proste
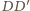 i
i
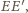 jest
środkiem jednokładności w skali
jest
środkiem jednokładności w skali
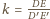 przekształcającej trójkąt
przekształcającej trójkąt
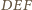 na trójkąt
na trójkąt
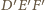 (
(
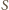 leży też na prostej
leży też na prostej
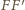 ).
).
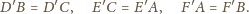
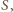 w skali
w skali
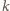 przekształca okrąg
przekształca okrąg
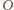 opisany na trójkącie
opisany na trójkącie
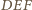 na okrąg
na okrąg
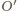 opisany na trójkącie
opisany na trójkącie
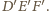 Środek okręgu
Środek okręgu
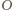 leży na prostopadłych do prostych
leży na prostopadłych do prostych
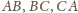 przechodzących
przez wierzchołki
przechodzących
przez wierzchołki
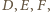 więc środek okręgu
więc środek okręgu
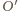 leży na
prostopadłych do prostych
leży na
prostopadłych do prostych
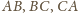 przechodzących przez wierzchołki
przechodzących przez wierzchołki
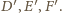 Na mocy lematu (dowód w artykule) te prostopadłe są
symetralnymi boków trójkąta
Na mocy lematu (dowód w artykule) te prostopadłe są
symetralnymi boków trójkąta
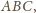 więc ich punkt wspólny to
środek okręgu opisanego na trójkącie
więc ich punkt wspólny to
środek okręgu opisanego na trójkącie
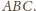
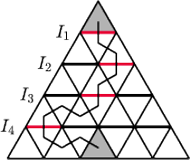
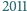 podzielono na
jednostkowe trójkąty równoboczne, analogicznie do rysunku 2. Ile jest
ścieżek prowadzących od trójkąta w górnym rzędzie do środkowego
trójkąta w dolnym rzędzie, takich że kolejne trójkąty na ścieżce mają
wspólny bok, a ścieżka nigdy nie wraca do góry (z rzędu niższego do
wyższego) ani nie przechodzi dwa razy przez żaden trójkąt?
podzielono na
jednostkowe trójkąty równoboczne, analogicznie do rysunku 2. Ile jest
ścieżek prowadzących od trójkąta w górnym rzędzie do środkowego
trójkąta w dolnym rzędzie, takich że kolejne trójkąty na ścieżce mają
wspólny bok, a ścieżka nigdy nie wraca do góry (z rzędu niższego do
wyższego) ani nie przechodzi dwa razy przez żaden trójkąt?
 na jeden sposób,
na jeden sposób,
 na
2 sposoby,
na
2 sposoby,
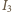 na 3 itd., wreszcie
na 3 itd., wreszcie
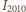 na 2010 sposobów. Zatem
ścieżek jest co najwyżej
na 2010 sposobów. Zatem
ścieżek jest co najwyżej
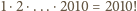 – nietrudno
zobaczyć, że jest ich dokładnie tyle, gdyż każdy wybór jednego z
– nietrudno
zobaczyć, że jest ich dokładnie tyle, gdyż każdy wybór jednego z
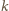 pododcinków odcinka
pododcinków odcinka
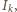 który ma przeciąć ścieżka,
definiuje poprawną ścieżkę.
który ma przeciąć ścieżka,
definiuje poprawną ścieżkę.
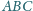 o kącie prostym przy
wierzchołku
o kącie prostym przy
wierzchołku
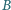 i boku
i boku
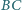 długości
długości
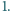 Punkty
Punkty
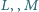 i
i
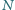 to odpowiednio środki boków
to odpowiednio środki boków
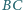 ,
,
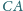 i
i
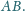 . Wiedząc, że proste
. Wiedząc, że proste
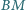 i
i
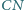 są prostopadłe,
obliczyć długość odcinka
są prostopadłe,
obliczyć długość odcinka
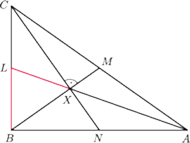
 środek ciężkości trójkąta
środek ciężkości trójkąta
 czyli
punkt przecięcia odcinków
czyli
punkt przecięcia odcinków
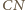 i
i
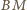 . Zauważmy, że
. Zauważmy, że
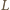 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
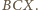 Zatem
Zatem
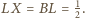 Ponieważ
Ponieważ
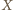 jest środkiem ciężkości, więc
jest środkiem ciężkości, więc
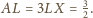
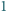 znajdują się punkty
znajdują się punkty
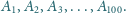 Udowodnij, że na brzegu tego koła istnieje taki
punkt
Udowodnij, że na brzegu tego koła istnieje taki
punkt
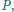 dla którego
dla którego

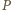 i
i
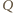 będą końcami dowolnej średnicy rozważanego
koła. Wtedy dla dowolnego punktu
będą końcami dowolnej średnicy rozważanego
koła. Wtedy dla dowolnego punktu
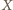 płaszczyzny mamy
płaszczyzny mamy
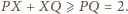 Nierówność ta jest tzw. nierównością
trójkąta dla trójki punktów
Nierówność ta jest tzw. nierównością
trójkąta dla trójki punktów
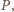
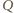 i
i
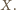 Więc dla
Więc dla
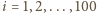 otrzymujemy
otrzymujemy
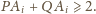
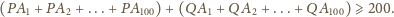
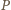 lub
lub
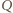 spełnia warunki zadania.
spełnia warunki zadania.
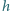 z wierzchołka
z wierzchołka
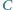 na podstawę
na podstawę
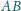 w trójkącie
w trójkącie
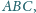 mając dane
mając dane
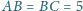 i
i
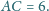
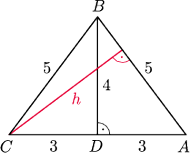
 było podstawą, i niech
było podstawą, i niech
 będzie
spodkiem wysokości z wierzchołka
będzie
spodkiem wysokości z wierzchołka
 Wtedy
Wtedy
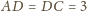 oraz
oraz
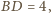 zatem
zatem
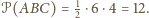 Ponieważ jednocześnie
Ponieważ jednocześnie
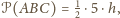 to
to
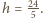
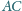 i
i
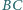 trójkąta równoramiennego
trójkąta równoramiennego
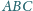 mają
długość 1. Dla jakiej podstawy
mają
długość 1. Dla jakiej podstawy
 pole tego trójkąta jest
maksymalne?
pole tego trójkąta jest
maksymalne?
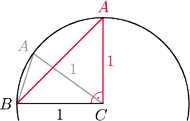
 było podstawą. Wtedy wierzchołek
było podstawą. Wtedy wierzchołek
 leży na okręgu o środku
leży na okręgu o środku
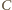 i promieniu 1. Pole trójkąta jest
maksymalne, gdy wysokość z
i promieniu 1. Pole trójkąta jest
maksymalne, gdy wysokość z
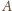 jest maksymalna (bo podstawa
jest maksymalna (bo podstawa
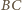 ma ustaloną długość 1), czyli gdy wysokość ta jest równa 1.
Zachodzi to dla
ma ustaloną długość 1), czyli gdy wysokość ta jest równa 1.
Zachodzi to dla
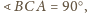 czyli dla
czyli dla
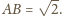
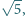
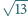 i
i
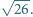
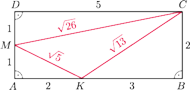
 o bokach
o bokach
 i
i
 Niech
punkt
Niech
punkt
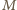 będzie środkiem boku
będzie środkiem boku
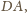 a punkt
a punkt
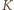 niech należy
do boku
niech należy
do boku
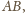 przy czym
przy czym
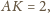
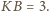 Wtedy z twierdzenia
Pitagorasa
Wtedy z twierdzenia
Pitagorasa
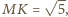
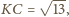
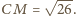 Należy
obliczyć pole trójkąta
Należy
obliczyć pole trójkąta
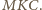 Jest ono równe
Jest ono równe
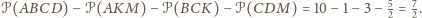
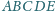 kąty przy wierzchołkach
kąty przy wierzchołkach
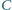 i
i
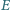 są proste. Oblicz
są proste. Oblicz
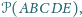 jeśli
jeśli
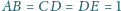 oraz
oraz
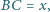
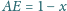 dla
dla
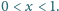
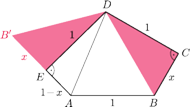
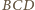 obok trójkąta
obok trójkąta
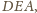 jak na rysunku
(
jak na rysunku
(
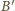 oznacza odpowiednik wierzchołka
oznacza odpowiednik wierzchołka
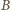 ). Wtedy w trójkącie
). Wtedy w trójkącie
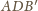 podstawa
podstawa
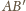 ma długość
ma długość
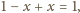 wysokość
wysokość
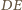 jest równa 1, więc pole jest równe
jest równa 1, więc pole jest równe
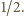 Pozostałą
częścią pięciokąta jest trójkąt
Pozostałą
częścią pięciokąta jest trójkąt
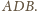 Przystaje on do trójkąta
Przystaje on do trójkąta
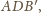 ponieważ
ponieważ
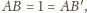
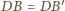 oraz bok
oraz bok
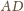 jest wspólny. Stąd
jest wspólny. Stąd
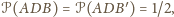 więc pole
pięciokąta równe jest 1.
więc pole
pięciokąta równe jest 1.
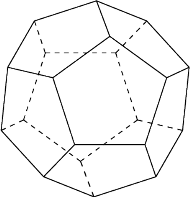
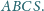 Krawędzie podstawy mają
długości
Krawędzie podstawy mają
długości
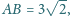
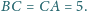 Krawędzie boczne mają
długości
Krawędzie boczne mają
długości
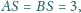
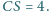 Oblicz objętość tego
ostrosłupa.
Oblicz objętość tego
ostrosłupa.
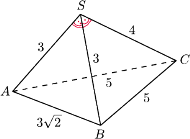
 jest trójkątem o bokach długości
jest trójkątem o bokach długości
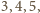 ma zatem
kąt prosty przy wierzchołku
ma zatem
kąt prosty przy wierzchołku
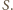 Analogicznie
Analogicznie
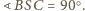 Ściana
Ściana
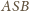 ma boki długości
ma boki długości
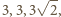 czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
 Ustawmy dany
ostrosłup inaczej: niech
Ustawmy dany
ostrosłup inaczej: niech
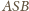 będzie podstawą. Wobec powyższych
obserwacji
będzie podstawą. Wobec powyższych
obserwacji
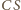 jest wtedy wysokością i
jest wtedy wysokością i
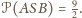 Stąd
objętość ostrosłupa to
Stąd
objętość ostrosłupa to
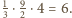
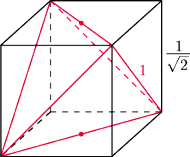
 Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
 , w którym pola trójkątów
, w którym pola trójkątów
 ,
,
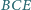 ,
,
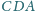 ,
,
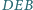 i
i
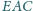 są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
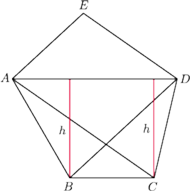
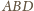 i
i
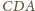 mają równe pola oraz wspólny
bok
mają równe pola oraz wspólny
bok
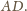 Wobec tego wysokości tych trójkątów poprowadzone do
boku
Wobec tego wysokości tych trójkątów poprowadzone do
boku
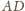 są równe. Ponadto punkty
są równe. Ponadto punkty
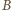 i
i
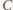 leżą po
tej samej stronie prostej
leżą po
tej samej stronie prostej
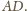 Stąd wniosek, że przekątna
Stąd wniosek, że przekątna
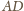 jest
równoległa do boku
jest
równoległa do boku
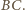 Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
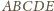 są równoległe do odpowiednich jego
boków
są równoległe do odpowiednich jego
boków
 leży wewnątrz czworościanu
leży wewnątrz czworościanu
 Dowieść,
że
Dowieść,
że

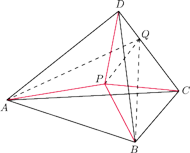
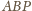 przecina krawędź
przecina krawędź
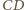 w punkcie
w punkcie
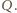 Stosując twierdzenie 1, otrzymujemy
Stosując twierdzenie 1, otrzymujemy
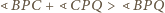
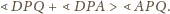
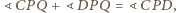 więc dostajemy
więc dostajemy
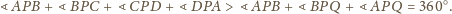
 będzie dowolnym punktem wewnątrz czworościanu
będzie dowolnym punktem wewnątrz czworościanu
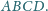 Dowieść, że
Dowieść, że

 Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
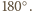 W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
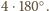 Sprzeczność, gdyż ta suma jest równa
Sprzeczność, gdyż ta suma jest równa
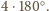
 kąty
kąty
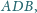
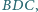
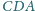 są
rozwarte, a krawędzie
są
rozwarte, a krawędzie
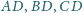 są równe. Dowieść, że trójkąt
są równe. Dowieść, że trójkąt
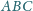 jest ostrokątny.
jest ostrokątny.
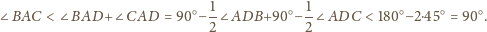
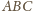 są ostre.
są ostre.
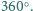
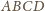 jest figurą złożoną z odcinków
jest figurą złożoną z odcinków
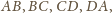 zaś suma jego kątów jest równa sumie kątów
płaskich utworzonych przez każde trzy kolejne jego wierzchołki
zaś suma jego kątów jest równa sumie kątów
płaskich utworzonych przez każde trzy kolejne jego wierzchołki
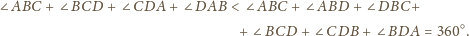
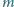 będzie liczbą krawędzi czworościanu o długości
będzie liczbą krawędzi czworościanu o długości
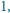 a
a
 liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
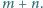
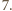
 w którym
w którym
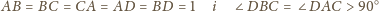
 Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
 Wynika stąd w szczególności, że liczba krawędzi
długości
Wynika stąd w szczególności, że liczba krawędzi
długości
 jest równa co najmniej
jest równa co najmniej
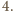 Jeśli jest
Jeśli jest
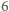 krawędzi
długości
krawędzi
długości
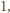 to nie ma kątów rozwartych. Jeśli jest
to nie ma kątów rozwartych. Jeśli jest
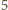 krawędzi
długości
krawędzi
długości
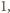 to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
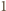 musi być równa
musi być równa
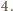 Tym samym
liczba kątów rozwartych musi być równa
Tym samym
liczba kątów rozwartych musi być równa
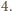 Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
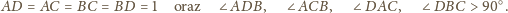
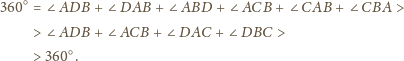
 będzie dowolnym punktem wewnątrz czworościanu
będzie dowolnym punktem wewnątrz czworościanu
 Dowieść, że
Dowieść, że

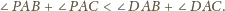
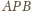 przecina krawędź
przecina krawędź
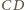 w
punkcie
w
punkcie
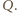 Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
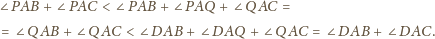
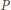 leży wewnątrz trójkąta
leży wewnątrz trójkąta
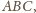 to
to
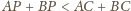 –
wystarczy rozważyć sferę o środku
–
wystarczy rozważyć sferę o środku
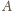 i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
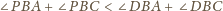
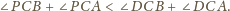
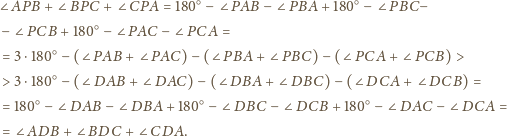
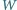 zawarta jest półprosta
zawarta jest półprosta
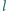 przechodząca
przez jego wierzchołek. Dowieść, że suma kątów utworzonych przez prostą
przechodząca
przez jego wierzchołek. Dowieść, że suma kątów utworzonych przez prostą
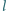 z krawędziami kąta
z krawędziami kąta
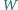 nie przekracza sumy kątów płaskich kąta
nie przekracza sumy kątów płaskich kąta
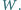
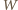 jest wierzchołkiem danego kąta trójściennego,
jest wierzchołkiem danego kąta trójściennego,
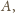
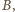
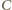 – dowolnymi punktami leżącymi na różnych
krawędziach tego kąta, zaś
– dowolnymi punktami leżącymi na różnych
krawędziach tego kąta, zaś
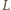 dowolnym punktem na półprostej
dowolnym punktem na półprostej
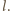 Mamy udowodnić, że
Mamy udowodnić, że
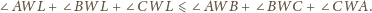
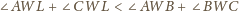
 pokryje się z jednym z ramion kąta, a ponadto
pozostałe dwa ramiona również się pokryją.
pokryje się z jednym z ramion kąta, a ponadto
pozostałe dwa ramiona również się pokryją.