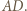Kochajcie trygonometrię, dziewczęta»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Kochajcie trygonometrię, dziewczęta
- Publikacja w Delcie: luty 2020
- Publikacja elektroniczna: 1 lutego 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)
Ustalmy półproste 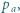
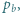
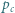 i
i 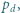 mające wspólny początek
mające wspólny początek 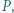 które zostały podane w kolejności antyzegarowej. Prosta
które zostały podane w kolejności antyzegarowej. Prosta 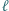 przecina je odpowiednio w punktach
przecina je odpowiednio w punktach 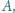
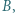
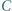 i
i 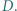 Dowieść, że wartość wyrażenia
Dowieść, że wartość wyrażenia 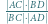 nie zależy od wyboru prostej
nie zależy od wyboru prostej 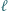 (niezmienniczość dwustosunku).
(niezmienniczość dwustosunku).

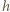 będzie odległością punktu
będzie odległością punktu 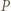 od prostej
od prostej 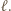 Oznaczmy przez
Oznaczmy przez 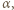
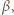
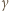 kąty pomiędzy półprostymi odpowiednio
kąty pomiędzy półprostymi odpowiednio 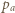 i
i 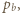
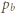 i
i 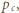
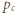 i
i 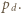 Wówczas obliczając na dwa sposoby pole trójkąta
Wówczas obliczając na dwa sposoby pole trójkąta 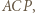 otrzymamy
otrzymamy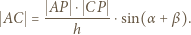
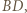
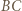 i
i