Mały wybór? I dobrze!»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Mały wybór? I dobrze!
- Publikacja w Delcie: listopad 2015
- Publikacja elektroniczna: 01-11-2015
- Artykuł źródłowy w wersji do druku [application/pdf]: (96 KB)
W czworokącie 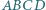 punkty
punkty 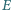 i
i 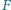 są środkami boków
są środkami boków 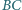 i
i 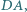 ponadto
ponadto 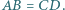 Wykaż, że prosta
Wykaż, że prosta 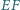 tworzy z prostymi
tworzy z prostymi 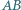 i
i 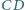 równe kąty.
równe kąty.
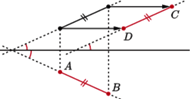
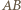 na
na 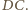 Na mocy
Na mocy 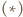 jej osią jest prosta
jej osią jest prosta 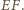 Prosta
Prosta 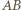 i jej obraz (prosta równoległa do
i jej obraz (prosta równoległa do 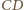 ) tworzą z osią symetrii równe kąty, co kończy dowód.
) tworzą z osią symetrii równe kąty, co kończy dowód.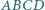 i
i 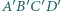 są przeciwnie zorientowane. Udowodnij, że środki odcinków
są przeciwnie zorientowane. Udowodnij, że środki odcinków 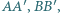
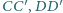 są współliniowe.
są współliniowe.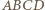 na
na 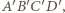 a następnie wykorzystać uwagę (*).
a następnie wykorzystać uwagę (*).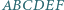 zachodzą równości
zachodzą równości 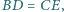
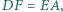
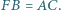 Wykaż, że symetralne boków
Wykaż, że symetralne boków  przecinają się w jednym punkcie.
przecinają się w jednym punkcie.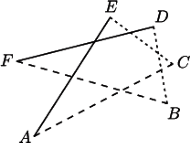
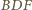 i
i 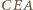 są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki
są przystające i tak samo zorientowane, istnieje więc izometria zachowująca orientację, która przeprowadza jeden z nich na drugi. Odcinki 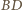 i
i 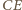 przecinają się, jako przekątne czworokąta wypukłego
przecinają się, jako przekątne czworokąta wypukłego 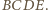 Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez
Stąd rozważana izometria jest obrotem; oznaczmy jego środek przez 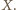
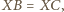 czyli punkt
czyli punkt 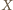 leży na symetralnej odcinka
leży na symetralnej odcinka 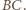 Analogicznie leży też na symetralnych
Analogicznie leży też na symetralnych 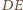 i
i 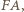 co kończy dowód.
co kończy dowód.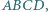 że
że 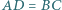 oraz boki
oraz boki 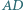 i
i 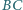 nie są równoległe. Zmienne punkty
nie są równoległe. Zmienne punkty 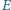 i
i 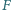 należą odpowiednio do boków
należą odpowiednio do boków 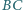 i
i 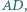 przy czym
przy czym 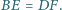 Proste
Proste 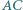 i
i 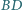 przecinają się w punkcie
przecinają się w punkcie 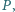 proste
proste 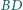 i
i 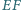 w punkcie
w punkcie 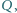 a proste
a proste 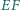 i
i 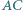 - w punkcie
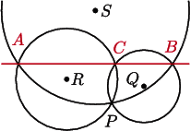
- w punkcie 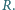 Wykaż, że okręgi opisane na trójkątach
Wykaż, że okręgi opisane na trójkątach 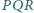 mają wspólny punkt różny od
mają wspólny punkt różny od 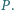
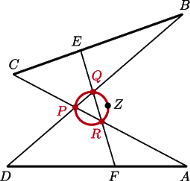
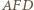 na
na 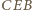 ; oznaczmy jego środek przez
; oznaczmy jego środek przez 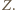 Podobnie jak w rozwiązaniu zadania 3, punkt
Podobnie jak w rozwiązaniu zadania 3, punkt 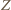 należy do symetralnych odcinków
należy do symetralnych odcinków 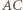 i
i 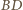 (a więc nie zależy od wyboru punktów
(a więc nie zależy od wyboru punktów 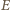 i
i 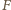 ) oraz do symetralnej
) oraz do symetralnej 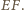 Stąd rzutami punktu
Stąd rzutami punktu 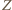 na odcinki
na odcinki 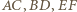 są ich środki.
są ich środki.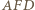 na
na 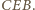 Na mocy (*), środki odcinków
Na mocy (*), środki odcinków 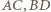 i
i 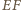 są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu
są wówczas współliniowe. Wykazaliśmy, że są to rzuty punktu 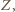 więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt
więc korzystając z twierdzenia o prostej Simsona uzyskujemy wniosek, iż stały punkt 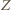 leży na każdym z okręgów opisanych na zmiennych trójkątach
leży na każdym z okręgów opisanych na zmiennych trójkątach 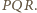
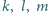 przecinają się w jednym punkcie
przecinają się w jednym punkcie 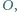 a punkt
a punkt 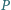 nie należy do żadnej z nich. Punkty
nie należy do żadnej z nich. Punkty 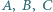 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu 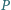 na proste
na proste 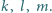 Udowodnij, że rzuty prostokątne
Udowodnij, że rzuty prostokątne 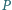 na proste
na proste 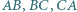 są współliniowe.
są współliniowe.
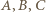 leży na okręgu o średnicy
leży na okręgu o średnicy 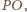 zatem punkt
zatem punkt 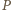 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 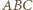 i teza wynika z twierdzenia o prostej Simsona.
i teza wynika z twierdzenia o prostej Simsona.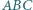 punkty
punkty 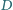 i
i 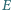 są spodkami wysokości
są spodkami wysokości 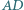 i
i 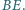 Dwa boki prostokąta
Dwa boki prostokąta 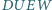 są zawarte w prostych
są zawarte w prostych 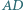 i
i 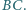 Prosta
Prosta 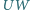 przecina bok
przecina bok 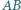 w punkcie
w punkcie 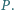 Wykaż, że proste
Wykaż, że proste 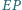 i
i 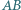 są prostopadłe.
są prostopadłe.
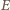 należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 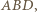 bowiem
bowiem 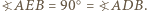 Stąd na mocy twierdzenia o prostej Simsona rzut punktu
Stąd na mocy twierdzenia o prostej Simsona rzut punktu 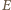 na prostą
na prostą 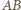 należy do prostej
należy do prostej 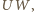 a więc jest nim punkt
a więc jest nim punkt 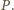
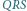
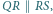
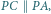
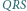
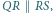
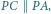
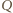 i
i 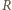 leżą na symetralnej odcinka
leżą na symetralnej odcinka 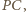 więc rzutem punktu
więc rzutem punktu 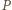 na prostą
na prostą 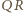 jest środek
jest środek 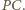 Podobnie dla
Podobnie dla 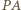 i
i 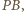 więc rzuty
więc rzuty 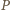 na proste zawierające boki trójkąta
na proste zawierające boki trójkąta 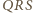 leżą na jednej prostej (równoległej do
leżą na jednej prostej (równoległej do 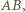 dwukrotnie bliżej punktu
dwukrotnie bliżej punktu 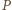 ) i teza wynika z twierdzenia o prostej Simsona.
) i teza wynika z twierdzenia o prostej Simsona.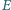 należy do boku
należy do boku 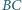 kwadratu
kwadratu 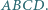 Punkty
Punkty 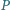 i
i 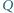 są rzutami prostokątnymi odpowiednio punktów
są rzutami prostokątnymi odpowiednio punktów 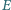 i
i 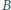 na proste
na proste 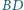 i
i 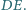 Udowodnij, że punkty
Udowodnij, że punkty 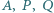 leżą na jednej prostej.
leżą na jednej prostej.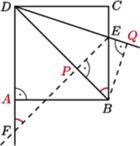
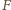 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 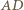 i
i 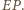 Wówczas
Wówczas 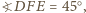 gdyż pozostałe dwa kąty trójkąta
gdyż pozostałe dwa kąty trójkąta 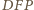 mają
mają 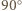 i
i 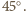 Ponieważ również
Ponieważ również 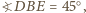 punkty
punkty 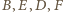 leżą na jednym okręgu. Teza wynika z twierdzenia o prostej Simsona dla trójkąta
leżą na jednym okręgu. Teza wynika z twierdzenia o prostej Simsona dla trójkąta 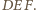
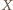 będzie punktem przecięcia dwóch z danych prostych. Pozostałe dwie proste nie są równoległe, stąd dwa trójkąty o wierzchołku
będzie punktem przecięcia dwóch z danych prostych. Pozostałe dwie proste nie są równoległe, stąd dwa trójkąty o wierzchołku 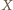 nie są jednokładne, więc opisane na nich okręgi nie są styczne w
nie są jednokładne, więc opisane na nich okręgi nie są styczne w 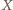 i mają drugi punkt wspólny
i mają drugi punkt wspólny 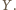
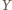 na wszystkie dane proste są współliniowe. Znów na mocy tego twierdzenia, punkt
na wszystkie dane proste są współliniowe. Znów na mocy tego twierdzenia, punkt 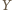 należy wówczas także do pozostałych dwóch z danych okręgów.
należy wówczas także do pozostałych dwóch z danych okręgów.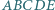 będzie wypukłym pięciokątem wpisanym w półkole o średnicy
będzie wypukłym pięciokątem wpisanym w półkole o średnicy 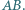 Punkty
Punkty 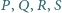 to rzuty punktu
to rzuty punktu 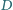 odpowiednio na proste
odpowiednio na proste 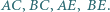 Udowodnij, że proste
Udowodnij, że proste 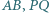 i
i 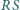 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.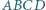 jest wpisany w okrąg i
jest wpisany w okrąg i 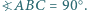 Punkty
Punkty 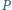 i
i 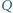 są rzutami prostokątnymi punktu
są rzutami prostokątnymi punktu 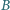 odpowiednio na proste
odpowiednio na proste 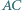 i
i 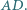 Wykaż, że prosta
Wykaż, że prosta 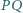 przechodzi przez środek odcinka
przechodzi przez środek odcinka 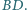
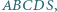 którego podstawą jest prostokąt
którego podstawą jest prostokąt 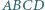 i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość
i którego każde dwie krawędzie boczne są różnych długości, a ponadto spełniona jest równość 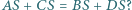 Odpowiedź uzasadnij.
Odpowiedź uzasadnij.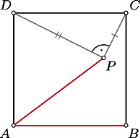
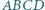 wybrano taki punkt
wybrano taki punkt 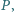 że
że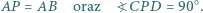
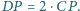
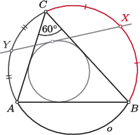
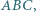 w którym
w którym 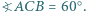 Na trójkącie tym opisano okrąg
Na trójkącie tym opisano okrąg 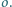 Punkt
Punkt 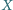 jest środkiem tego łuku
jest środkiem tego łuku 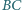 okręgu
okręgu 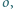 który nie zawiera punktu
który nie zawiera punktu 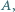 a punkt
a punkt 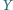 jest środkiem tego łuku
jest środkiem tego łuku 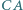 okręgu
okręgu 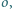 który nie zawiera punktu
który nie zawiera punktu 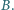 Udowodnij, że prosta
Udowodnij, że prosta 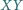 jest styczna do okręgu wpisanego w trójkąt
jest styczna do okręgu wpisanego w trójkąt 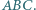
 -kąta foremnego rozmieszczono liczby
-kąta foremnego rozmieszczono liczby 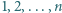 w taki sposób, że suma liczb znajdujących się w każdych trzech kolejnych wierzchołkach
w taki sposób, że suma liczb znajdujących się w każdych trzech kolejnych wierzchołkach  -kąta jest parzysta. Wyznacz wszystkie liczby naturalne
-kąta jest parzysta. Wyznacz wszystkie liczby naturalne 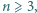 dla których takie rozmieszczenie jest możliwe.
dla których takie rozmieszczenie jest możliwe.
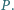 Poprowadzono styczną do mniejszego z nich w pewnym punkcie
Poprowadzono styczną do mniejszego z nich w pewnym punkcie 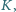 przecinającą większy okrąg w punktach
przecinającą większy okrąg w punktach 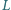 i
i 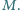 Udowodnić, że
Udowodnić, że 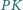 jest dwusieczną kąta
jest dwusieczną kąta 
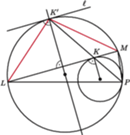
 przeprowadzającą mniejszy okrąg na większy. Obrazem prostej
przeprowadzającą mniejszy okrąg na większy. Obrazem prostej 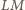 jest prosta
jest prosta 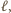 równoległa do
równoległa do 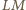 i styczna do większego okręgu w pewnym punkcie
i styczna do większego okręgu w pewnym punkcie 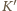 (obrazie punktu
(obrazie punktu 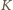 ). Punkty
). Punkty 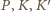 są współliniowe. Ponieważ
są współliniowe. Ponieważ 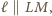 punkty
punkty 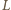 i
i 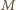 są symetryczne względem średnicy większego okręgu przechodzącej przez
są symetryczne względem średnicy większego okręgu przechodzącej przez 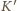 i zachodzi równość
i zachodzi równość 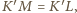 więc
więc 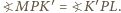
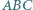 jest styczny do boków
jest styczny do boków 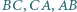 odpowiednio w punktach
odpowiednio w punktach 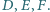 Prosta równoległa do
Prosta równoległa do 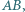 przechodząca przez punkt
przechodząca przez punkt 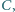 przecina proste
przecina proste 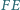 i
i 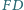 odpowiednio w punktach
odpowiednio w punktach 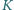 i
i 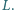 Udowodnij, że na czworokącie
Udowodnij, że na czworokącie 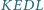 można opisać okrąg.
można opisać okrąg.
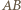 i
i 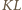 oraz z twierdzenia (*) uzyskujemy
oraz z twierdzenia (*) uzyskujemy 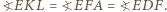 Stąd
Stąd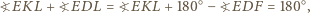
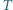 jest wpisany w okrąg
jest wpisany w okrąg 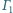 oraz opisany na okręgu
oraz opisany na okręgu 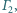 przy czym
przy czym 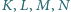 są kolejnymi punktami styczności
są kolejnymi punktami styczności 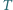 z
z 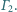 Wykaż, że
Wykaż, że 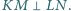
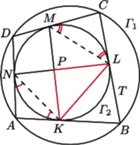
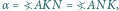
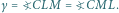
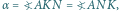
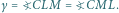
 jest wpisany w okrąg, to
jest wpisany w okrąg, to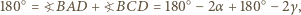
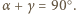
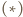 dla okręgu
dla okręgu 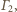 mamy
mamy 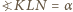 oraz
oraz 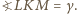 Wobec tego
Wobec tego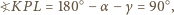
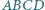 i taki punkt
i taki punkt 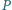 w jego wnętrzu, dla którego
w jego wnętrzu, dla którego 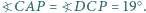 Wyznacz
Wyznacz 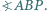
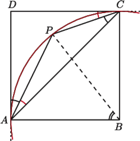
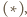 prosta
prosta 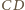 jest styczna do okręgu opisanego na trójkącie
jest styczna do okręgu opisanego na trójkącie 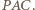 Wobec tego środek tego okręgu leży na prostej
Wobec tego środek tego okręgu leży na prostej 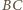 (bo
(bo 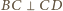 ). Analogicznie prosta
). Analogicznie prosta 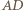 także jest styczna do tego okręgu, gdyż
także jest styczna do tego okręgu, gdyż 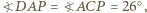 zatem środek rozważanego okręgu leży też na prostej
zatem środek rozważanego okręgu leży też na prostej 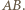 Stąd jest nim punkt
Stąd jest nim punkt 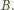
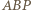 jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany
jest więc kątem środkowym opartym na tym samym łuku, co kąt wpisany 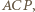 zatem
zatem 
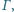 wpisany w trójkąt
wpisany w trójkąt 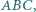 jest styczny do boków
jest styczny do boków 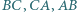 odpowiednio w punktach
odpowiednio w punktach 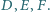 Wykaż, że środki
Wykaż, że środki 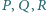 okręgów wpisanych w trójkąty
okręgów wpisanych w trójkąty 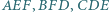 leżą na okręgu
leżą na okręgu 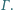
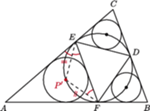
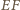 okręgu
okręgu 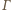 przez
przez 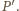 Wówczas
Wówczas 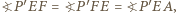 przy czym druga równość wynika z twierdzenia
przy czym druga równość wynika z twierdzenia 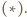 Wobec tego
Wobec tego 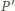 leży na dwusiecznej kąta
leży na dwusiecznej kąta 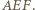 Analogicznie dla kąta
Analogicznie dla kąta 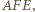 więc
więc 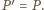 Dowód dla punktów
Dowód dla punktów 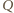 i
i 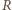 przebiega podobnie.
przebiega podobnie.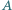 i
i 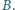 Proste styczne do tych okręgów w punkcie
Proste styczne do tych okręgów w punkcie 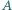 przecinają je w drugich punktach
przecinają je w drugich punktach 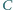 i
i 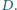 Wykaż, że
Wykaż, że 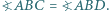
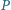 poprowadzono prostą przecinającą dany okrąg
poprowadzono prostą przecinającą dany okrąg 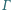 w punktach
w punktach 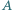 i
i 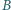 oraz prostą styczną do
oraz prostą styczną do 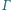 w punkcie
w punkcie 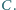 Wykaż, że
Wykaż, że 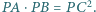
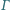 jest styczny do prostej
jest styczny do prostej 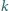 w punkcie
w punkcie 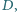 cięciwa
cięciwa 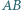 tego okręgu jest równoległa do
tego okręgu jest równoległa do 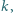 punkt
punkt 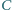 należy do prostej
należy do prostej 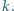 Proste
Proste 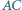 i
i 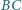 przecinają okrąg
przecinają okrąg 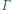 w drugich punktach
w drugich punktach 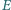 i
i 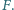 Wykaż, że prosta
Wykaż, że prosta 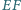 przechodzi przez środek odcinka
przechodzi przez środek odcinka 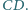
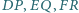 przecinają się w jednym punkcie
przecinają się w jednym punkcie 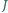 oraz że punkty
oraz że punkty 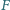 i
i 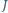 są symetryczne względem prostej
są symetryczne względem prostej 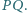
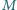 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku 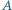 poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 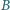 i
i 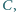 wyznacza trójkąt
wyznacza trójkąt 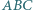 o najmniejszym polu.
o najmniejszym polu.

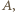 a jego przekątne przecinają się w punkcie
a jego przekątne przecinają się w punkcie 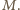 Przekątna tego równoległoboku, która przecina ramiona kąta (w punktach
Przekątna tego równoległoboku, która przecina ramiona kąta (w punktach 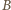 i
i 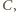
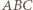 o najmniejszym polu.
o najmniejszym polu.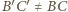 jest inną prostą przechodzącą przez punkt
jest inną prostą przechodzącą przez punkt 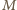 (na przykład taką, że
(na przykład taką, że 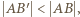
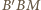 i
i 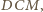 mamy:
mamy: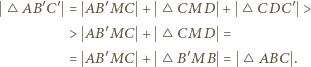
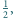 a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2.
a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2.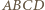 i w nim trójkąt
i w nim trójkąt 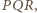 którego wierzchołki leżą na różnych bokach kwadratu tak, że
którego wierzchołki leżą na różnych bokach kwadratu tak, że 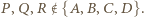 Wówczas trójkąt
Wówczas trójkąt 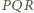 łatwo zastąpić trójkątem o większej wysokości, czyli większym polu (
łatwo zastąpić trójkątem o większej wysokości, czyli większym polu (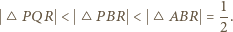


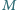 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku 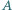 poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 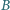 i
i 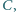 wyznacza trójkąt
wyznacza trójkąt 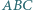 o najmniejszym obwodzie.
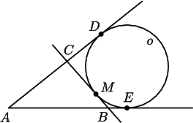
o najmniejszym obwodzie.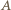 wpisujemy dwa okręgi przechodzące przez punkt
wpisujemy dwa okręgi przechodzące przez punkt 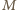 (
(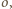 w punkcie
w punkcie 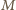 wyznaczamy styczną, która przecina ramiona kąta w punktach
wyznaczamy styczną, która przecina ramiona kąta w punktach 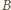 i
i 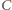 (
(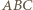 spełnia warunki zadania i ma najmniejszy obwód równy
spełnia warunki zadania i ma najmniejszy obwód równy 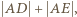 gdzie
gdzie 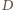 i
i 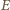 to punkty styczności okręgu
to punkty styczności okręgu  z ramionami kąta (jest tak, bo
z ramionami kąta (jest tak, bo 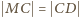 i
i 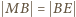 ).
).
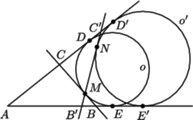
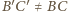 jest inną prostą zawierającą punkt
jest inną prostą zawierającą punkt 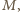 to okrąg
to okrąg 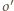 dopisany do trójkąta
dopisany do trójkąta 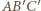 jest styczny do ramion kąta w punktach
jest styczny do ramion kąta w punktach 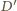 i
i 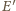 oraz do odcinka
oraz do odcinka 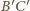 w punkcie
w punkcie 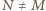 (
(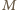 leży na zewnątrz okręgu dopisanego
leży na zewnątrz okręgu dopisanego 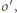 więc okrąg
więc okrąg 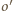 ma większy promień niż okrąg
ma większy promień niż okrąg  i obwód trójkąta
i obwód trójkąta 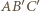 jest równy
jest równy 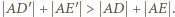
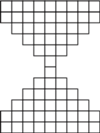
 figurę przedstawioną na rysunku?
figurę przedstawioną na rysunku? zawiera jedno pole białe i jedno czarne, to różnica między liczbą pól białych i czarnych w każdej połowie figury powinna być równa zero, a w naszym przypadku wynosi 4.
zawiera jedno pole białe i jedno czarne, to różnica między liczbą pól białych i czarnych w każdej połowie figury powinna być równa zero, a w naszym przypadku wynosi 4.