Jeszcze o taliach
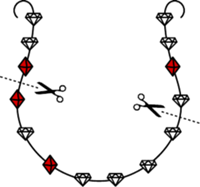
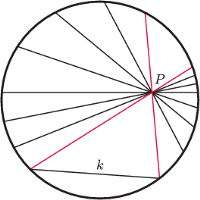
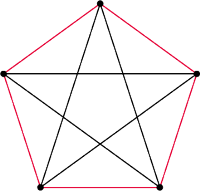
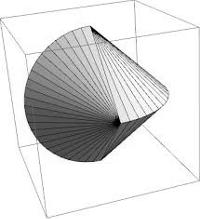
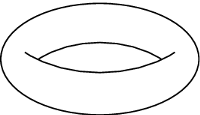
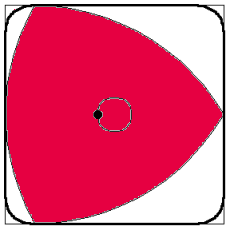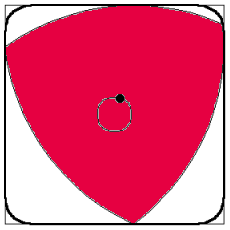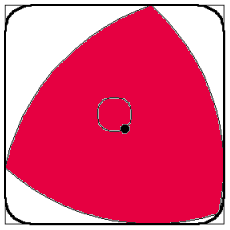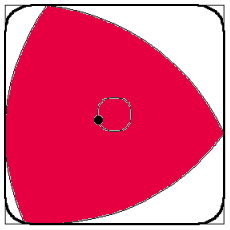
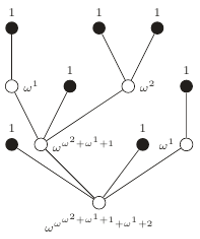
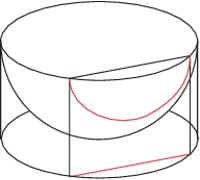
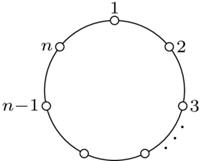
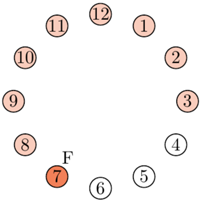
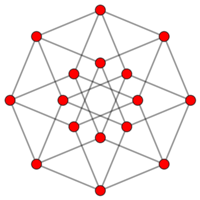
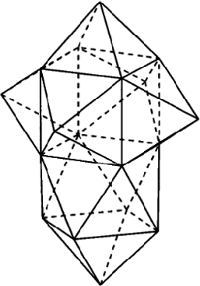
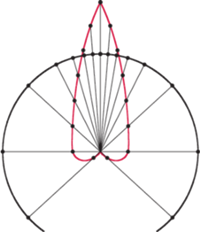
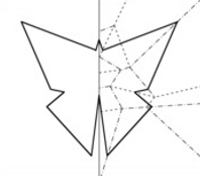
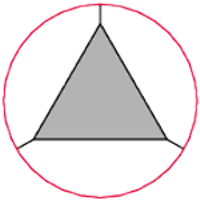
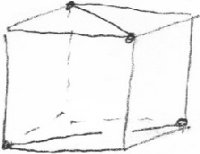
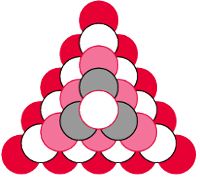
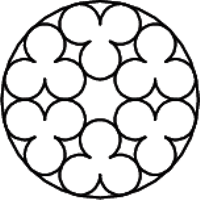
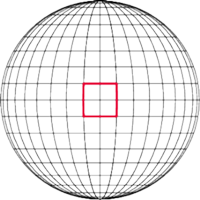
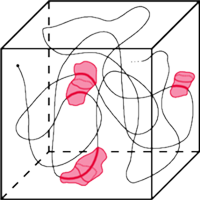
W znakomitym artykule O wieszaniu bombek na choince, (Delta 12/2011), Krzysztof Rudnik definiuje talie: talia jakiejś bryły to najmniejszy okrąg otaczający ją i niedający się z niej zsunąć. Kluczowymi bohaterami opowieści są foremne antygraniastosłupy.