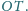Załóżmy, że trójkąt przystający do
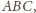 o wszystkich wierzchołkach
zielonych, nie istnieje. Rozważymy trzy przypadki.
o wszystkich wierzchołkach
zielonych, nie istnieje. Rozważymy trzy przypadki.
Jeżeli istnieje trójkąt przystający do
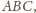 o wszystkich wierzchołkach
czerwonych – nazwijmy go po prostu
o wszystkich wierzchołkach
czerwonych – nazwijmy go po prostu
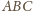 – przesuwamy go o dowolny
wektor długości 1. Otrzymujemy trójkąt
– przesuwamy go o dowolny
wektor długości 1. Otrzymujemy trójkąt
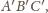 który (w myśl
przyjętego założenia) ma co najmniej jeden wierzchołek czerwony. Wraz
z odpowiednim punktem z trójki
który (w myśl
przyjętego założenia) ma co najmniej jeden wierzchołek czerwony. Wraz
z odpowiednim punktem z trójki
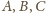 tworzy on czerwoną parę
punktów odległych o 1.
tworzy on czerwoną parę
punktów odległych o 1.
Jeżeli istnieje trójkąt przystający do
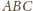 (ponownie nazwijmy go
(ponownie nazwijmy go
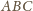 ), w którym dokładnie jeden wierzchołek – na przykład
), w którym dokładnie jeden wierzchołek – na przykład
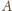 –
jest zielony, rysujemy dowolny trójkąt równoboczny
–
jest zielony, rysujemy dowolny trójkąt równoboczny
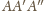 o boku
długości 1. Przesuwamy trójkąt
o boku
długości 1. Przesuwamy trójkąt
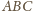 o wektory
o wektory
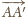 i
i
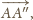 otrzymując trójkąty
otrzymując trójkąty
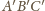 i
i
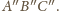 Gdy któryś
z punktów
Gdy któryś
z punktów
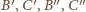 jest czerwony, mamy tezę. Gdy te cztery punkty
są zielone, wówczas (znów na mocy przyjętego założenia) punkty
jest czerwony, mamy tezę. Gdy te cztery punkty
są zielone, wówczas (znów na mocy przyjętego założenia) punkty
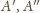 muszą być czerwone, co też daje tezę.
muszą być czerwone, co też daje tezę.
Pozostaje przypadek, gdy w każdym trójkącie przystającym do
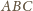 dokładnie jeden wierzchołek jest czerwony. Ustalmy dowolny czerwony
punkt
dokładnie jeden wierzchołek jest czerwony. Ustalmy dowolny czerwony
punkt
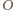 na płaszczyźnie i narysujmy dowolny trójkąt przystający
do
na płaszczyźnie i narysujmy dowolny trójkąt przystający
do
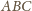 (ponownie nazwijmy go
(ponownie nazwijmy go
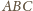 ), z wierzchołkiem
), z wierzchołkiem
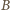 w owym punkcie
w owym punkcie
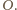 Punkty
Punkty
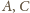 są więc zielone.
Uzupełniamy trójkąt
są więc zielone.
Uzupełniamy trójkąt
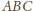 do równoległoboku
do równoległoboku
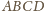 ; trójkąt
; trójkąt
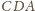 przystaje do
przystaje do
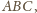 więc punkt
więc punkt
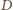 musi być
czerwony. Długość
musi być
czerwony. Długość
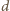 odcinka
odcinka
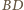 jest liczbą określoną
jednoznacznie przez zadany trójkąt
jest liczbą określoną
jednoznacznie przez zadany trójkąt
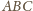 (to podwojona długość
środkowej z wierzchołka
(to podwojona długość
środkowej z wierzchołka
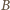 ). Z dowolności usytuowania trójkąta
). Z dowolności usytuowania trójkąta
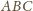 (z wierzchołkiem
(z wierzchołkiem
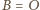 ) wynika, że każdy punkt
położony w odległości
) wynika, że każdy punkt
położony w odległości
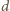 od punktu
od punktu
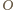 jest czerwony.
jest czerwony.
Ponieważ punkt
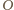 mógł być dowolnym punktem czerwonym,
widzimy, że każdy odcinek długości
mógł być dowolnym punktem czerwonym,
widzimy, że każdy odcinek długości
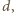 z jednym końcem
czerwonym, ma i drugi koniec czerwony. Krokiem długości
z jednym końcem
czerwonym, ma i drugi koniec czerwony. Krokiem długości
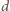 można
połączyć każde dwa punkty płaszczyzny – cała płaszczyzna jest więc czerwona.
To oczywiście także daje tezę.
można
połączyć każde dwa punkty płaszczyzny – cała płaszczyzna jest więc czerwona.
To oczywiście także daje tezę.
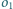 i
i
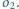 Znajdź inwersję przekształcającą
Znajdź inwersję przekształcającą
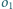 na
na
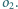
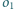 i
i
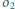 będą rozłącznymi okręgami, takimi że
będą rozłącznymi okręgami, takimi że
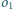 leży we wnętrzu
leży we wnętrzu
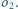 Rysujemy okrąg
Rysujemy okrąg
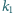 styczny
zewnętrznie do
styczny
zewnętrznie do
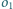 i wewnętrznie do
i wewnętrznie do
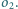 Następnie rysujemy okrąg
Następnie rysujemy okrąg
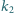 styczny zewnętrznie do
styczny zewnętrznie do
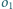 i
i
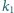 oraz wewnętrznie do
oraz wewnętrznie do
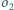 itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
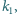 to mówimy, że okręgi
to mówimy, że okręgi
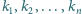 tworzą
łańcuch Steinera okręgów
tworzą
łańcuch Steinera okręgów
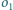 i
i
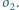 Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
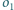 i
i
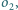 to jest to niezależne od
położenia pierwszego okręgu
to jest to niezależne od
położenia pierwszego okręgu
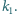
 i dwa rozłączne okręgi
i dwa rozłączne okręgi
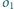 i
i
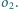 Narysuj
okrąg styczny do
Narysuj
okrąg styczny do
 i prostopadły do okręgów
i prostopadły do okręgów
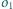 i
i
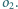
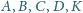 będą pięcioma różnymi punktami,
leżącymi na jednym okręgu. Odległości punktu
będą pięcioma różnymi punktami,
leżącymi na jednym okręgu. Odległości punktu
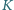 od prostych
od prostych
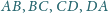 wynoszą odpowiednio
wynoszą odpowiednio
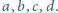 Znaleźć wzór
algebraiczny, pozwalający wyznaczyć dowolną z liczb
Znaleźć wzór
algebraiczny, pozwalający wyznaczyć dowolną z liczb
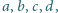 gdy
znane są trzy pozostałe.
gdy
znane są trzy pozostałe.
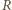 będzie promieniem danego okręgu – opisanego na każdym
z trójkątów
będzie promieniem danego okręgu – opisanego na każdym
z trójkątów
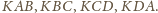 Zachodzi równość
Zachodzi równość
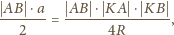
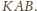 Po uproszczeniu
dostajemy pierwszą z wypisanych poniżej równości, a dalsze trzy są jej
cyklicznymi odpowiednikami:
Po uproszczeniu
dostajemy pierwszą z wypisanych poniżej równości, a dalsze trzy są jej
cyklicznymi odpowiednikami:
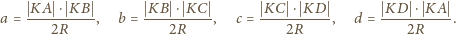
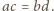
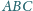 kąt przy wierzchołku
kąt przy wierzchołku
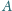 ma większą miarę niż
kąt przy wierzchołku
ma większą miarę niż
kąt przy wierzchołku
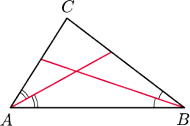
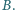 Wykazać, że dwusieczna poprowadzona
z wierzchołka
Wykazać, że dwusieczna poprowadzona
z wierzchołka
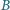 jest dłuższa niż dwusieczna poprowadzona
z wierzchołka
jest dłuższa niż dwusieczna poprowadzona
z wierzchołka
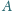 .
.
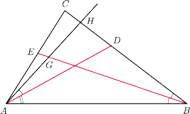
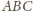 mamy
mamy
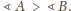 Odłóżmy
kąt
Odłóżmy
kąt
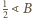 na dwusiecznej
na dwusiecznej
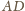 jako na ramieniu, jak na rysunku.
jako na ramieniu, jak na rysunku.
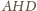 i
i
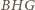 mamy
mamy
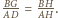 Ale
w trójkącie
Ale
w trójkącie
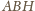 bok
bok
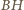 leży naprzeciw większego kąta niż
bok
leży naprzeciw większego kąta niż
bok
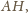 więc
więc
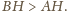 Stąd i z uzyskanej proporcji
otrzymujemy
Stąd i z uzyskanej proporcji
otrzymujemy
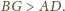 Tym bardziej więc
Tym bardziej więc
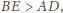 co
mieliśmy udowodnić.
co
mieliśmy udowodnić.
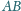 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego
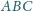 wybrano punkt
wybrano punkt
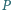 . Niech
. Niech
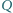 i
i
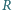 będą rzutami
prostokątnymi punktu
będą rzutami
prostokątnymi punktu
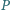 na boki
na boki
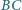 i
i
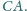 Udowodnić,
że pole którejś z figur
Udowodnić,
że pole którejś z figur
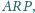
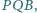
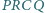 stanowi
co najmniej
stanowi
co najmniej
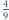 pola trójkąta
pola trójkąta
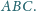
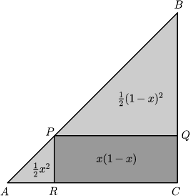
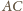 trójkąta
trójkąta
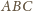 wynosi
wynosi
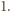 Oznaczmy
Oznaczmy
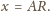
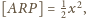
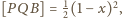
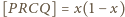 jest niemniejsza
od
jest niemniejsza
od
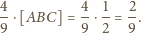
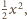
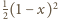 były mniejsze od
były mniejsze od
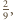 to
byłoby
to
byłoby
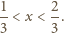
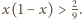
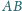 i
i
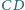 przecinają się w punkcie
przecinają się w punkcie
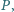 przy czym
przy czym
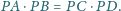 Wykaż, że punkty
Wykaż, że punkty
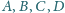 leżą na
jednym okręgu.
leżą na
jednym okręgu.
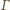 opisany na trójkącie
opisany na trójkącie
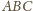 przecina prostą
przecina prostą
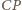 w drugim punkcie
w drugim punkcie
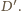 Wtedy
Wtedy
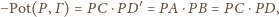
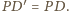 Oba punkty
Oba punkty
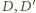 leżą na prostej
leżą na prostej
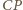 po
tej samej stronie
po
tej samej stronie
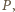 więc
więc
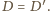
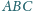 wysokość z wierzchołka
wysokość z wierzchołka
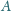 przecina okrąg o średnicy
przecina okrąg o średnicy
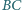 w punktach
w punktach
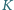 i
i
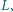 a wysokość z wierzchołka
a wysokość z wierzchołka
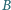 przecina okrąg o średnicy
przecina okrąg o średnicy
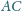 w punktach
w punktach
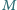 i
i
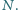 Wykaż, że punkty
Wykaż, że punkty
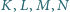 leżą na jednym okręgu.
leżą na jednym okręgu.
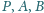 leżą w tej kolejności na prostej, punkt
leżą w tej kolejności na prostej, punkt
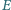 – poza nią.
Wykaż, że jeśli
– poza nią.
Wykaż, że jeśli
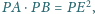 to prosta
to prosta
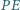 jest styczna do
okręgu opisanego na
jest styczna do
okręgu opisanego na
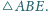
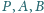 leżą w tej kolejności na prostej. Wyznacz zbiór
punktów styczności prostych przechodzących przez
leżą w tej kolejności na prostej. Wyznacz zbiór
punktów styczności prostych przechodzących przez
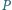 do okręgów
przechodzących przez
do okręgów
przechodzących przez
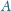 i
i
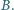
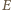 będzie jednym z rozważanych punktów styczności,
wtedy
będzie jednym z rozważanych punktów styczności,
wtedy
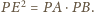 Takie punkty leżą więc na okręgu
Takie punkty leżą więc na okręgu
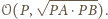 Z kolei z zadania 4, każdy punkt z tego okręgu
i spoza prostej
Z kolei z zadania 4, każdy punkt z tego okręgu
i spoza prostej
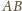 należy do szukanego zbioru.
należy do szukanego zbioru.
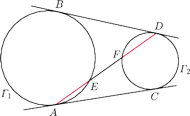
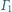 i
i
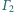 są rozłączne zewnętrznie. Wspólne styczne,
nierozdzielające ich, są styczne do
są rozłączne zewnętrznie. Wspólne styczne,
nierozdzielające ich, są styczne do
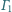 w punktach
w punktach
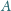 i
i
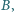 a do
a do
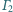 – odpowiednio w
– odpowiednio w
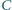 i
i
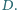 Odcinek
Odcinek
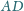 przecina okręgi
przecina okręgi
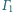 i
i
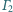 odpowiednio w
odpowiednio w
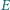 i
i
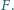 Wykaż, że
Wykaż, że
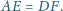
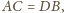 to
to
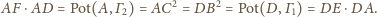
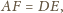 więc też
więc też
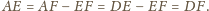
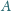 i
i
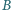 leżą po różnych stronach prostej
leżą po różnych stronach prostej
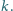 Skonstruuj taki okrąg, przechodzący przez punkty
Skonstruuj taki okrąg, przechodzący przez punkty
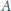 i
i
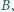 aby długość jego cięciwy
aby długość jego cięciwy
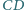 wyznaczonej przez prostą
wyznaczonej przez prostą
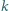 była minimalna.
była minimalna.
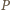 będzie punktem przecięcia prostej
będzie punktem przecięcia prostej
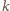 i odcinka
i odcinka
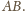 Wartość
Wartość
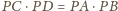 nie zależy od wyboru okręgu.
Z nierówności średnich
nie zależy od wyboru okręgu.
Z nierówności średnich
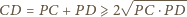
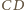 jest minimalna), gdy
jest minimalna), gdy
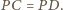 Jak skonstruować taki okrąg?
Jak skonstruować taki okrąg?
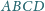 jest wpisany w okrąg. Punkt
jest wpisany w okrąg. Punkt
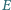 jest
środkiem cięciwy
jest
środkiem cięciwy
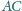 oraz
oraz
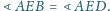 Wykaż, że
Wykaż, że
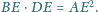
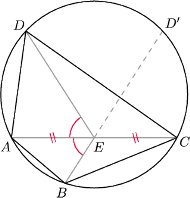
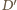 będzie drugim punktem przecięcia prostej
będzie drugim punktem przecięcia prostej
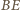 i okręgu.
Wtedy
i okręgu.
Wtedy
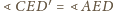 oraz
oraz
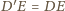 (dlaczego?).
(dlaczego?).
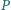 na zewnątrz tego okręgu. Skonstruuj punkty styczności okręgu
z prostymi przechodzącymi przez
na zewnątrz tego okręgu. Skonstruuj punkty styczności okręgu
z prostymi przechodzącymi przez
 wiedząc, że punkty te mieszczą się
na kartce.
wiedząc, że punkty te mieszczą się
na kartce.
 przecinającą dany łuk w dwóch punktach.
przecinającą dany łuk w dwóch punktach.
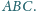 Dowieść, że istnieje trójkąt przystający do
Dowieść, że istnieje trójkąt przystający do
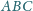 o wszystkich wierzchołkach zielonych lub istnieje odcinek
długości jednostkowej o obu końcach czerwonych.
o wszystkich wierzchołkach zielonych lub istnieje odcinek
długości jednostkowej o obu końcach czerwonych.
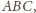 o wszystkich wierzchołkach
zielonych, nie istnieje. Rozważymy trzy przypadki.
o wszystkich wierzchołkach
zielonych, nie istnieje. Rozważymy trzy przypadki.
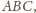 o wszystkich wierzchołkach
czerwonych – nazwijmy go po prostu
o wszystkich wierzchołkach
czerwonych – nazwijmy go po prostu
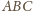 – przesuwamy go o dowolny
wektor długości 1. Otrzymujemy trójkąt
– przesuwamy go o dowolny
wektor długości 1. Otrzymujemy trójkąt
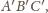 który (w myśl
przyjętego założenia) ma co najmniej jeden wierzchołek czerwony. Wraz
z odpowiednim punktem z trójki
który (w myśl
przyjętego założenia) ma co najmniej jeden wierzchołek czerwony. Wraz
z odpowiednim punktem z trójki
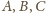 tworzy on czerwoną parę
punktów odległych o 1.
tworzy on czerwoną parę
punktów odległych o 1.
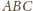 (ponownie nazwijmy go
(ponownie nazwijmy go
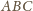 ), w którym dokładnie jeden wierzchołek – na przykład
), w którym dokładnie jeden wierzchołek – na przykład
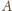 –
jest zielony, rysujemy dowolny trójkąt równoboczny
–
jest zielony, rysujemy dowolny trójkąt równoboczny
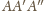 o boku
długości 1. Przesuwamy trójkąt
o boku
długości 1. Przesuwamy trójkąt
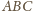 o wektory
o wektory
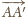 i
i
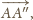 otrzymując trójkąty
otrzymując trójkąty
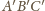 i
i
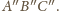 Gdy któryś
z punktów
Gdy któryś
z punktów
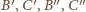 jest czerwony, mamy tezę. Gdy te cztery punkty
są zielone, wówczas (znów na mocy przyjętego założenia) punkty
jest czerwony, mamy tezę. Gdy te cztery punkty
są zielone, wówczas (znów na mocy przyjętego założenia) punkty
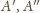 muszą być czerwone, co też daje tezę.
muszą być czerwone, co też daje tezę.
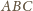 dokładnie jeden wierzchołek jest czerwony. Ustalmy dowolny czerwony
punkt
dokładnie jeden wierzchołek jest czerwony. Ustalmy dowolny czerwony
punkt
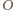 na płaszczyźnie i narysujmy dowolny trójkąt przystający
do
na płaszczyźnie i narysujmy dowolny trójkąt przystający
do
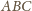 (ponownie nazwijmy go
(ponownie nazwijmy go
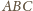 ), z wierzchołkiem
), z wierzchołkiem
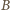 w owym punkcie
w owym punkcie
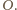 Punkty
Punkty
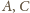 są więc zielone.
Uzupełniamy trójkąt
są więc zielone.
Uzupełniamy trójkąt
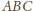 do równoległoboku
do równoległoboku
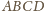 ; trójkąt
; trójkąt
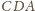 przystaje do
przystaje do
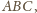 więc punkt
więc punkt
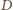 musi być
czerwony. Długość
musi być
czerwony. Długość
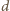 odcinka
odcinka
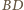 jest liczbą określoną
jednoznacznie przez zadany trójkąt
jest liczbą określoną
jednoznacznie przez zadany trójkąt
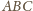 (to podwojona długość
środkowej z wierzchołka
(to podwojona długość
środkowej z wierzchołka
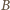 ). Z dowolności usytuowania trójkąta
). Z dowolności usytuowania trójkąta
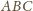 (z wierzchołkiem
(z wierzchołkiem
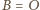 ) wynika, że każdy punkt
położony w odległości
) wynika, że każdy punkt
położony w odległości
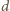 od punktu
od punktu
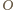 jest czerwony.
jest czerwony.
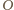 mógł być dowolnym punktem czerwonym,
widzimy, że każdy odcinek długości
mógł być dowolnym punktem czerwonym,
widzimy, że każdy odcinek długości
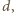 z jednym końcem
czerwonym, ma i drugi koniec czerwony. Krokiem długości
z jednym końcem
czerwonym, ma i drugi koniec czerwony. Krokiem długości
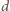 można
połączyć każde dwa punkty płaszczyzny – cała płaszczyzna jest więc czerwona.
To oczywiście także daje tezę.
można
połączyć każde dwa punkty płaszczyzny – cała płaszczyzna jest więc czerwona.
To oczywiście także daje tezę.
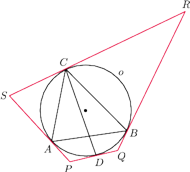
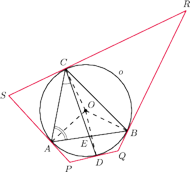
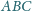 opisano okrąg
opisano okrąg
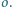 Punkt
Punkt
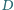 jest punktem przecięcia środkowej poprowadzonej z wierzchołka
jest punktem przecięcia środkowej poprowadzonej z wierzchołka
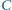 z okręgiem
z okręgiem
 . W punktach
. W punktach
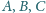 i
i
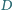 poprowadzono
styczne do
poprowadzono
styczne do
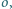 które wyznaczyły czworokąt
które wyznaczyły czworokąt
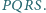 Udowodnić,
że na czworokącie
Udowodnić,
że na czworokącie
 można opisać okrąg wtedy i tylko wtedy, gdy
trójkąt
można opisać okrąg wtedy i tylko wtedy, gdy
trójkąt
 jest równoramienny.
jest równoramienny.
 środek okręgu
środek okręgu
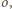 przez
przez
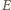 zaś
środek odcinka
zaś
środek odcinka
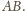 Na czworokącie
Na czworokącie
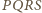 można opisać
okrąg wtedy i tylko wtedy, gdy
można opisać
okrąg wtedy i tylko wtedy, gdy
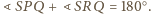 Rozważając
czworokąty
Rozważając
czworokąty
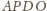 i
i
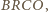 widzimy, że jest to równoważne
temu, iż
widzimy, że jest to równoważne
temu, iż
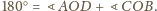 Ale
Ale

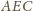 ma kąt prosty przy wierzchołku
ma kąt prosty przy wierzchołku
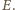 Wobec definicji punktu
Wobec definicji punktu
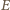 jest to prawda wtedy i tylko wtedy, gdy trójkąt
jest to prawda wtedy i tylko wtedy, gdy trójkąt
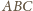 jest
równoramienny o podstawie
jest
równoramienny o podstawie

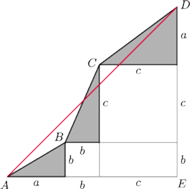
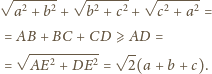

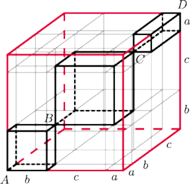
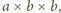
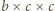 oraz
oraz
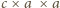 tak, jak na rysunku. Wówczas
tak, jak na rysunku. Wówczas
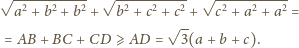
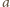 i
i
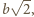
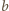 i
i
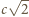 oraz
oraz
 i
i
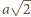 tak, jak na rysunku (do poprzedniego
zadania).
tak, jak na rysunku (do poprzedniego
zadania).
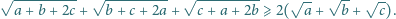
 oraz
oraz
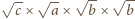 analogicznie
do sytuacji z rysunku do poprzedniego zadania. Wtedy
analogicznie
do sytuacji z rysunku do poprzedniego zadania. Wtedy
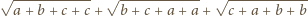
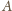 do
do
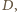 natomiast odcinek
natomiast odcinek
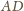 to przekątna 4-wymiarowego hipersześcianu o krawędzi
to przekątna 4-wymiarowego hipersześcianu o krawędzi
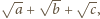 czyli
czyli
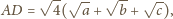
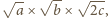
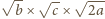 oraz
oraz
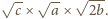

 i 1,
i 1,
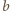 i 1
oraz
i 1
oraz
 i 1 podobnie, jak na rysunku. Wtedy
i 1 podobnie, jak na rysunku. Wtedy
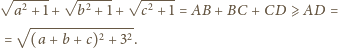
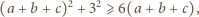
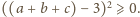

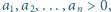 takich, że
takich, że
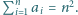
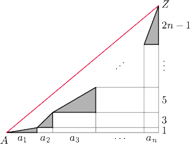
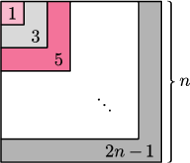
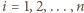 ustawmy trójkąty prostokątne o przyprostokątnych
ustawmy trójkąty prostokątne o przyprostokątnych
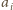 oraz
oraz
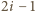 tak, jak na
tak, jak na 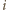 -tego trójkąta ma wtedy długość
-tego trójkąta ma wtedy długość
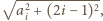 więc dla
łamanej od
więc dla
łamanej od
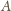 do
do
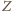 uzyskujemy
uzyskujemy
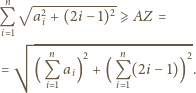
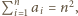 a
a 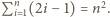 Stąd
Stąd
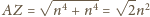 i to jest szukana
najmniejsza wartość danego wyrażenia. Jest ona osiągana, gdy łamana od
i to jest szukana
najmniejsza wartość danego wyrażenia. Jest ona osiągana, gdy łamana od
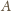 do
do
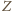 jest odcinkiem, czyli gdy
jest odcinkiem, czyli gdy
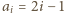 dla każdego
dla każdego
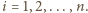



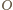 i promieniu
i promieniu
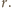 Wybierzmy jedną ze ścian, styczną do owej
kuli w punkcie
Wybierzmy jedną ze ścian, styczną do owej
kuli w punkcie
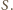 Rzut kuli na płaszczyznę tej ściany jest kołem
Rzut kuli na płaszczyznę tej ściany jest kołem
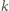 o środku
o środku
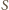 i promieniu
i promieniu
 (rysunek powyżej
przedstawia przekrój płaszczyzną, przechodzącą przez prostą
(rysunek powyżej
przedstawia przekrój płaszczyzną, przechodzącą przez prostą
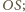 odcinek
odcinek
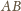 jest średnicą koła
jest średnicą koła
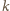 ).
).
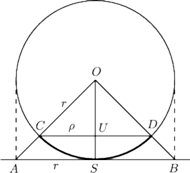
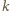 i wierzchołku
i wierzchołku
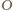 wycina na powierzchni kuli
wycina na powierzchni kuli
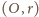 obszar
obszar
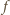 – czaszę kulistą, ograniczoną okręgiem, którego
średnicą jest (na rysunku) odcinek
– czaszę kulistą, ograniczoną okręgiem, którego
średnicą jest (na rysunku) odcinek
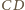 o środku
o środku
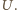 Czasze,
uzyskane w ten sposób dla ośmiu ścian, są rozłącznymi obszarami na sferze.
Suma ich pól nie przekracza pola całej sfery, równego
Czasze,
uzyskane w ten sposób dla ośmiu ścian, są rozłącznymi obszarami na sferze.
Suma ich pól nie przekracza pola całej sfery, równego
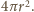 Wszelako
koło o średnicy
Wszelako
koło o średnicy
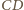 jest podstawą stożka, z wierzchołkiem w punkcie
jest podstawą stożka, z wierzchołkiem w punkcie
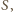 o promieniu podstawy
o promieniu podstawy
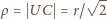 i wysokości
i wysokości
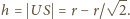 Powierzchnia boczna tego stożka ma pole
Powierzchnia boczna tego stożka ma pole
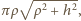 czyli
czyli
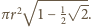 Powierzchnia obszaru
Powierzchnia obszaru
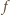 jest
jeszcze większa. Wychodzi nierówność
jest
jeszcze większa. Wychodzi nierówność
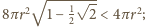 po przekształceniu:
po przekształceniu:
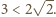 Sprzeczność; zatem taki ośmiościan
nie istnieje.
Sprzeczność; zatem taki ośmiościan
nie istnieje.
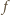 wynosi
wynosi
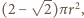 co jest większe niż
co jest większe niż
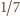 pola całej sfery; wielościan
o rozważanej własności może mieć więc co najwyżej sześć ścian).
pola całej sfery; wielościan
o rozważanej własności może mieć więc co najwyżej sześć ścian).
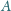 i
i
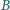 . Dany jest też kąt
skierowany
. Dany jest też kąt
skierowany
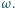 Przez
Przez
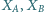 oznaczamy obraz punktu
oznaczamy obraz punktu
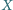 przy obrocie o kąt
przy obrocie o kąt
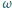 względem punktu
względem punktu
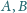 , odpowiednio.
Znaleźć wszystkie punkty
, odpowiednio.
Znaleźć wszystkie punkty
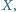 dla których trójkąt
dla których trójkąt
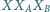 jest równoboczny.
jest równoboczny.
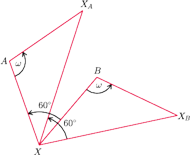
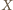 jest taki, że trójkąt
jest taki, że trójkąt
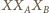 jest
równoboczny. Wówczas trójkąty
jest
równoboczny. Wówczas trójkąty
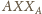 i
i
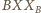 są przystające,
gdyż są podobne i
są przystające,
gdyż są podobne i
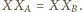 Ponieważ obrazem odcinka
Ponieważ obrazem odcinka
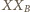 przy obrocie o kąt
przy obrocie o kąt
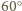 (skierowany zgodnie z kątem
(skierowany zgodnie z kątem
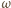 ) względem punktu
) względem punktu
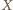 jest odcinek
jest odcinek
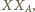 więc obrazem
trójkąta
więc obrazem
trójkąta
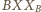 jest trójkąt
jest trójkąt
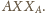 Zatem kąt
Zatem kąt
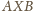 ma
miarę
ma
miarę
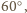 a ponadto
a ponadto
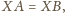 więc trójkąt
więc trójkąt
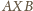 jest
równoboczny.
jest
równoboczny. 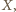 dla których trójkąt
dla których trójkąt
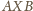 jest równoboczny.
Łatwo sprawdzić, że dla nich trójkąt
jest równoboczny.
Łatwo sprawdzić, że dla nich trójkąt
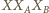 jest też równoboczny.
Zatem są to wszystkie szukane punkty.
jest też równoboczny.
Zatem są to wszystkie szukane punkty.
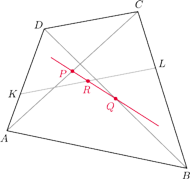
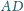 i
i
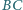 czworokąta wypukłego
czworokąta wypukłego
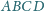 wybrano
takie punkty
wybrano
takie punkty
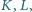 że
że
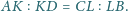 Wykaż, że środki
Wykaż, że środki
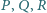 odcinków
odcinków
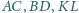 są współliniowe.
są współliniowe.
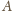 i
i
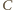 masy
masy
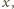 a w
a w
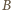 i
i
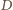 masy
masy
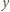 takie, by
takie, by
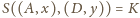 (da się takie masy
dobrać). Wtedy
(da się takie masy
dobrać). Wtedy
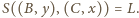 Wobec tego
Wobec tego
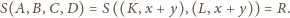
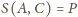 oraz
oraz
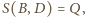 więc
więc
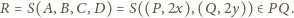
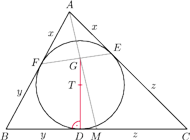
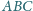 jest styczny do boków
jest styczny do boków
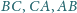 odpowiednio w punktach
odpowiednio w punktach
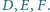 Punkt
Punkt
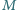 jest
środkiem boku
jest
środkiem boku
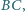 zaś odcinki
zaś odcinki
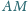 i
i
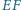 przecinają
się w punkcie
przecinają
się w punkcie
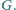 Wykaż, że proste
Wykaż, że proste
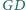 i
i
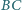 są
prostopadłe.
są
prostopadłe.
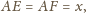
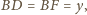
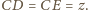 Umieśćmy w
Umieśćmy w
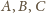 odpowiednio masy
odpowiednio masy
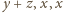 i wyznaczmy środek ciężkości
i wyznaczmy środek ciężkości
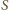 tego układu.
tego układu.
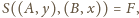
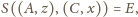 więc
więc
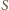 leży na prostej
leży na prostej
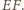 Jednocześnie
Jednocześnie
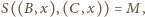 więc
więc
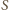 leży też na prostej
leży też na prostej
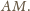 Stąd
Stąd
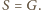
 w punkcie
w punkcie
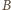 i masę
i masę
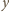 w punkcie
w punkcie
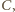 wtedy
wtedy
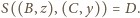 Niech
Niech
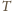 będzie środkiem ciężkości „starych” i „nowych” mas, wtedy
będzie środkiem ciężkości „starych” i „nowych” mas, wtedy
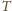 leży na prostej
leży na prostej
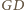 łączącej ich środki ciężkości.
łączącej ich środki ciężkości.
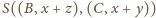 jest
jej spodkiem dla
jest
jej spodkiem dla
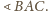 Leży więc na niej punkt
Leży więc na niej punkt
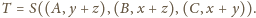 Analogicznie leży on też
na pozostałych dwusiecznych kątów trójkąta, jest zatem środkiem okręgu
wpisanego. Stąd
Analogicznie leży on też
na pozostałych dwusiecznych kątów trójkąta, jest zatem środkiem okręgu
wpisanego. Stąd
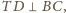 co kończy dowód.
co kończy dowód.
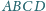 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku
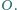 Przekątne
Przekątne
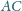 i
i
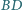 są prostopadłe i przecinają się w punkcie
są prostopadłe i przecinają się w punkcie
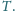 Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka
Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka