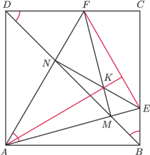
Obroty kwadratów»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Obroty kwadratów
- Publikacja w Delcie: marzec 2013
- Publikacja elektroniczna: 01-03-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
Punkty
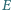 i
i
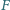 leżą odpowiednio na bokach
leżą odpowiednio na bokach
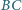 i
i
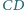 kwadratu
kwadratu
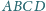 o boku 1, przy czym obwód
trójkąta
o boku 1, przy czym obwód
trójkąta
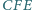 równy jest 2. Wyznacz miarę kąta
równy jest 2. Wyznacz miarę kąta
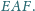
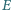 i
i
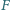 leżą odpowiednio na bokach
leżą odpowiednio na bokach
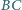 i
i
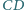 kwadratu
kwadratu
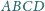 o boku 1, przy czym
o boku 1, przy czym
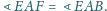 Wykaż, że
Wykaż, że
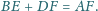
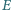 i
i
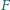 leżą odpowiednio na bokach
leżą odpowiednio na bokach
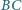 i
i
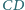 kwadratu
kwadratu
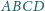 o boku 1, przy czym
o boku 1, przy czym
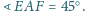 Oblicz wysokość trójkąta
Oblicz wysokość trójkąta
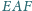 poprowadzoną
z wierzchołka
poprowadzoną
z wierzchołka
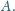
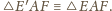 Wysokości tych
trójkątów poprowadzone z wierzchołka
Wysokości tych
trójkątów poprowadzone z wierzchołka
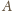 są więc obie równe
są więc obie równe
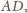 czyli 1.
czyli 1.
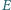 i
i
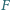 leżą odpowiednio na bokach
leżą odpowiednio na bokach
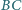 i
i
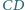 kwadratu
kwadratu
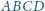 o boku 1, przy czym
o boku 1, przy czym
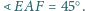 Proste
Proste
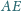 i
i
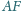 przecinają przekątną
przecinają przekątną
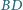 odpowiednio w punktach
odpowiednio w punktach
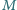 i
i
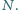 Proste
Proste
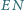 i
i
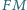 przecinają się w punkcie
przecinają się w punkcie
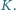 Wykaż, że proste
Wykaż, że proste
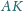 i
i
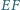 są prostopadłe.
są prostopadłe.
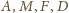 leżą na jednym okręgu, bo
leżą na jednym okręgu, bo
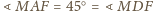 i punkty
i punkty
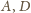 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej
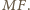 Kąt
Kąt
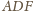 jest
prosty, więc
jest
prosty, więc
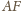 jest średnicą tego okręgu. Stąd
jest średnicą tego okręgu. Stąd
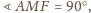 zatem
zatem
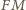 jest wysokością trójkąta
jest wysokością trójkąta
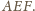 Analogicznie
Analogicznie
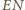 jest
wysokością tego trójkąta, więc
jest
wysokością tego trójkąta, więc
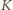 to jego ortocentrum. Wobec tego
to jego ortocentrum. Wobec tego
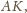 jako trzecia wysokość, jest prostopadła do
jako trzecia wysokość, jest prostopadła do
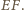
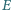 i
i
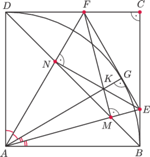
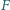 leżą odpowiednio na bokach
leżą odpowiednio na bokach
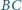 i
i
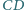 kwadratu
kwadratu
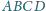 o boku 1, przy czym prosta
o boku 1, przy czym prosta
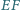 jest styczna do okręgu o środku
jest styczna do okręgu o środku
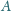 i promieniu 1. Proste
i promieniu 1. Proste
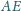 i
i
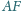 przecinają przekątną
przecinają przekątną
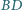 odpowiednio w punktach
odpowiednio w punktach
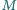 i
i
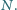 Udowodnij, że punkty
Udowodnij, że punkty
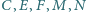 leżą na
jednym okręgu.
leżą na
jednym okręgu.
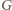 będzie punktem styczności prostej
będzie punktem styczności prostej
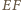 do danego
okręgu. Wtedy
do danego
okręgu. Wtedy
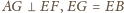 oraz
oraz
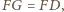 zatem
zatem
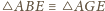 oraz
oraz
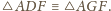 Stąd
Stąd
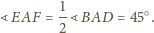
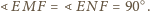
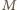 i
i
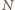 leżą na okręgu o średnicy
leżą na okręgu o średnicy
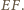 Leży na nim też punkt
Leży na nim też punkt
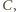 bo
bo
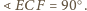
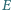 i
i
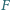 leżą odpowiednio na bokach
leżą odpowiednio na bokach
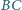 i
i
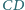 kwadratu
kwadratu
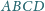 o boku 1, przy czym
o boku 1, przy czym
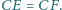 Punkt
Punkt
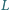 to rzut punktu
to rzut punktu
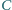 na prostą
na prostą
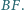 Wykaż, że
Wykaż, że
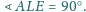
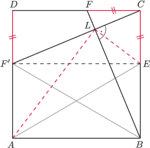
 wokół środka. Obrazem punktu
wokół środka. Obrazem punktu
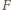 jest
taki punkt
jest
taki punkt
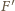 na boku
na boku
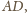 że
że
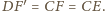 Obrazem
prostej
Obrazem
prostej
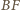 jest prosta
jest prosta
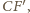 jest ona prostopadła do
jest ona prostopadła do
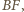 więc
zawiera punkt
więc
zawiera punkt
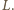 Opiszmy okrąg na prostokącie
Opiszmy okrąg na prostokącie
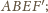 jego
średnicą jest
jego
średnicą jest
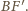 Punkt
Punkt
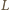 leży na tym okręgu, ponieważ kąt
leży na tym okręgu, ponieważ kąt
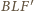 jest prosty. Średnicą okręgu jest także
jest prosty. Średnicą okręgu jest także
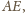 więc również
kąt
więc również
kąt
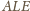 jest prosty.
jest prosty.
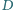 leży na boku
leży na boku
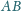 trójkąta
trójkąta
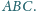 Punkt
Punkt
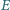 jest środkiem okręgu dopisanego, stycznego do boku
jest środkiem okręgu dopisanego, stycznego do boku
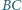 oraz
przedłużeń boków
oraz
przedłużeń boków
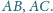 Punkt
Punkt
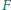 jest środkiem
okręgu wpisanego w trójkąt
jest środkiem
okręgu wpisanego w trójkąt
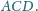 Dowieść, że jeżeli trójkąt
Dowieść, że jeżeli trójkąt
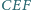 jest równoramienny, to także trójkąt
jest równoramienny, to także trójkąt
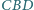 jest
równoramienny.
jest
równoramienny.
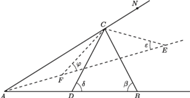
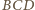 przy wierzchołkach
przy wierzchołkach
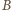 i
i
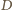 przez
przez
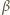 i
i
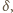 a miary kątów trójkąta
a miary kątów trójkąta
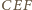 przy
wierzchołkach
przy
wierzchołkach
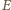 i
i
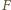 przez
przez
 i
i
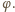
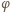 i
i
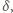 jako kąty zewnętrzne trójkątów
jako kąty zewnętrzne trójkątów
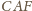 i
i
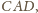 są związane zależnością
są związane zależnością
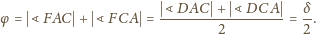
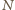 będzie dowolnym punktem na przedłużeniu boku
będzie dowolnym punktem na przedłużeniu boku
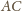 poza wierzchołek
poza wierzchołek
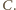 Kąty
Kąty
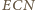 i
i
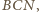 jako
kąty zewnętrzne trójkątów
jako
kąty zewnętrzne trójkątów
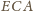 i
i
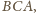 wyrażają się
jako sumy:
wyrażają się
jako sumy:
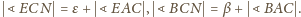 Tak
więc
Tak
więc
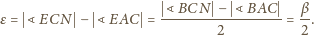
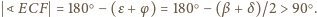 Zatem jeśli
trójkąt
Zatem jeśli
trójkąt
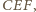 z kątem rozwartym przy wierzchołku
z kątem rozwartym przy wierzchołku
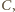 jest
równoramienny, to
jest
równoramienny, to
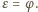 Z uzyskanych wcześniej równości
dostajemy wówczas
Z uzyskanych wcześniej równości
dostajemy wówczas
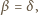 czyli równoramienność trójkąta
czyli równoramienność trójkąta
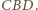
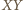 nazywamy płaszczyznę do niego
prostopadłą, przechodzącą przez jego środek.
nazywamy płaszczyznę do niego
prostopadłą, przechodzącą przez jego środek.
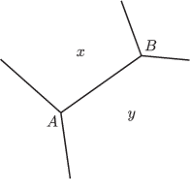
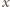 naszego wielościanu. Płaszczyzny
symetralne krawędzi tej ściany przecinają się wszystkie wzdłuż prostej
naszego wielościanu. Płaszczyzny
symetralne krawędzi tej ściany przecinają się wszystkie wzdłuż prostej
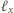 prostopadłej do ściany
prostopadłej do ściany
 i przechodzącej przez środek
okręgu opisanego na tej ścianie. Ta prosta jest zbiorem środków wszystkich
sfer zawierających wszystkie wierzchołki ściany
i przechodzącej przez środek
okręgu opisanego na tej ścianie. Ta prosta jest zbiorem środków wszystkich
sfer zawierających wszystkie wierzchołki ściany
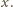
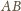 będzie wspólną krawędzią sąsiednich ścian
będzie wspólną krawędzią sąsiednich ścian
 i
i
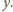 Proste
Proste
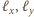 nie są równoległe i obie leżą
w płaszczyźnie symetralnej
nie są równoległe i obie leżą
w płaszczyźnie symetralnej
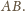 Przecinają się więc w jednym punkcie,
który jest środkiem sfery opisanej na ścianach
Przecinają się więc w jednym punkcie,
który jest środkiem sfery opisanej na ścianach
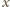 i
i
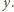
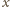 i
i
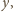 to
jej środek musi leżeć zarówno na prostej
to
jej środek musi leżeć zarówno na prostej
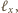 jak i na prostej
jak i na prostej
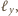 co dowodzi, że ta sfera jest wyznaczona jednoznacznie.
co dowodzi, że ta sfera jest wyznaczona jednoznacznie.

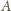 spotykają się trzy krawędzie, to w tym
wierzchołku spotykają się też trzy ściany. Oznaczmy je jak na rysunku.
spotykają się trzy krawędzie, to w tym
wierzchołku spotykają się też trzy ściany. Oznaczmy je jak na rysunku.
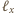 z płaszczyzną symetralną odcinka
z płaszczyzną symetralną odcinka
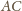 (przyjmujemy definicje i oznaczenia z rozwiązania zadania M
1375). Zauważmy, że należy on też do prostej
(przyjmujemy definicje i oznaczenia z rozwiązania zadania M
1375). Zauważmy, że należy on też do prostej
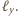 Istotnie,
należy do płaszczyzny symetralnej
Istotnie,
należy do płaszczyzny symetralnej
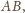 bo prosta
bo prosta
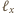 jest
w niej zawarta, i do płaszczyzny symetralnej
jest
w niej zawarta, i do płaszczyzny symetralnej
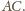 Przecięcie tych
płaszczyzn to właśnie prosta
Przecięcie tych
płaszczyzn to właśnie prosta
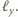 Podobnie, należy on do prostej
Podobnie, należy on do prostej
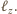 Jest więc równo odległy od wszystkich wierzchołków ścian
Jest więc równo odległy od wszystkich wierzchołków ścian
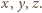
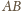 na tej ścieżce, że sfera zawierająca wierzchołki
ścian spotykających się w
na tej ścieżce, że sfera zawierająca wierzchołki
ścian spotykających się w
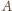 różni się od sfery, w którą są wpisane
ściany spotykające się w
różni się od sfery, w którą są wpisane
ściany spotykające się w
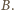 Ale to znaczy, że dla sąsiednich ścian
o wspólnej krawędzi
Ale to znaczy, że dla sąsiednich ścian
o wspólnej krawędzi
 istnieją dwie różne sfery, w które te ściany
są jednocześnie wpisane, co przeczy tezie zadania ZM-1375.
istnieją dwie różne sfery, w które te ściany
są jednocześnie wpisane, co przeczy tezie zadania ZM-1375.
 i takie punkty
i takie punkty
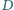 i
i
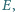 że
że
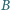 leży na odcinku
leży na odcinku
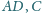 leży na odcinku
leży na odcinku
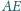 oraz
zachodzą równości
oraz
zachodzą równości
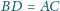 i
i
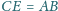 (rysunek). Symetralna
odcinka
(rysunek). Symetralna
odcinka
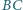 przecina
przecina
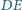 w punkcie
w punkcie
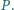 Udowodnić, że
kąty
Udowodnić, że
kąty
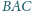 i
i
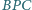 są równe.
są równe.
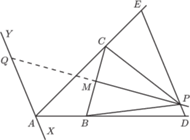
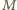 jest środkiem
jest środkiem
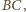 jego odległość od prostej
jego odległość od prostej
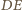 to średnia arytmetyczna odległości punktów
to średnia arytmetyczna odległości punktów
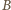 i
i
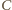 od
od
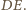 Jest ona równa średniej arytmetycznej odległości tych punktów
od
Jest ona równa średniej arytmetycznej odległości tych punktów
od
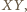 ponieważ
ponieważ
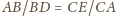 i
i
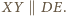 Zatem
Zatem
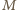 jest równo odległy od
jest równo odległy od
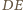 i
i
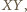 skąd
skąd
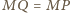 oraz
oraz
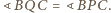
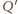 będzie takim punktem na półprostej
będzie takim punktem na półprostej
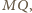 że
że
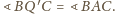 Z podobieństwa trójkątów równoramiennych
Z podobieństwa trójkątów równoramiennych
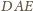 i
i
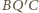 mamy
mamy
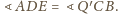 Zatem skoro na
czworokącie
Zatem skoro na
czworokącie
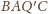 można opisać okrąg, to
można opisać okrąg, to
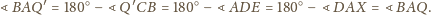
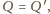 co daje tezę.
co daje tezę.
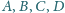 leżą, w tej właśnie kolejności, na prostej
leżą, w tej właśnie kolejności, na prostej
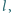 przy
czym
przy
czym
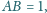
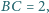
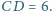 Rozstrzygnij, czy istnieje taki
punkt
Rozstrzygnij, czy istnieje taki
punkt
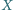 spoza prostej
spoza prostej
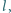 aby
aby
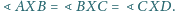

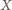 istnieje, to
istnieje, to
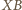 jest dwusieczną kąta
jest dwusieczną kąta
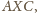 zatem z twierdzenia o dwusiecznej
zatem z twierdzenia o dwusiecznej
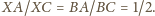 Punkty
Punkty
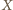 i
i
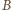 leżą więc na okręgu Apoloniusza dla punktów
leżą więc na okręgu Apoloniusza dla punktów
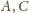 i stałej 1/2. Analogicznie punkty
i stałej 1/2. Analogicznie punkty
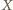 i
i
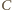 leżą na
okręgu Apoloniusza dla punktów
leżą na
okręgu Apoloniusza dla punktów
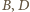 i stałej 1/3.
i stałej 1/3.

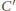 na prostej
na prostej
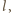 różny od
różny od
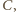 spełnia
warunek
spełnia
warunek
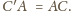 Wtedy
Wtedy
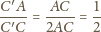
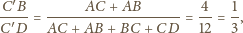
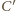 należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
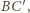 a drugiego –
a drugiego –
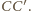 Stąd jedynym
ich wspólnym punktem jest
Stąd jedynym
ich wspólnym punktem jest
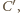 czyli
czyli
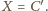 Ale wtedy
Ale wtedy
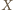 leży na prostej
leży na prostej
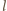 – sprzeczność.
– sprzeczność.
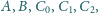 przy czym
przy czym
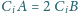 dla
dla
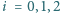 oraz
oraz
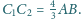 Udowodnij,
że kąt
Udowodnij,
że kąt
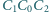 jest prosty i że punkty
jest prosty i że punkty
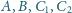 leżą na jednej
płaszczyźnie.
leżą na jednej
płaszczyźnie.

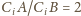 dla
dla
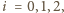 więc wszystkie punkty
więc wszystkie punkty
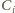 leżą na sferze Apoloniusza dla punktów
leżą na sferze Apoloniusza dla punktów
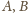 i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
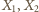 na prostej
na prostej
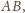 spełniające warunek
spełniające warunek
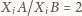 dla
dla
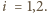 Wówczas
Wówczas
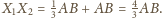
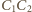 także jest średnicą rozważanej sfery. Stąd
kąt
także jest średnicą rozważanej sfery. Stąd
kąt
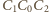 jest prosty, jako wpisany oparty na średnicy. Proste
jest prosty, jako wpisany oparty na średnicy. Proste
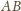 i
i
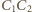 przecinają się (w środku sfery), więc punkty
przecinają się (w środku sfery), więc punkty
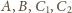 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
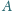 i
i
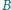 nie należą do płaszczyzny
nie należą do płaszczyzny
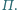 Wyznacz
zbiór wszystkich punktów
Wyznacz
zbiór wszystkich punktów
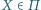 o tej własności, że proste
o tej własności, że proste
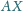 i
i
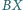 tworzą z płaszczyzną
tworzą z płaszczyzną
 równe kąty.
równe kąty.
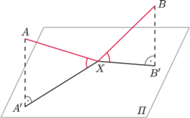
 oznaczają odpowiednio rzuty punktów
oznaczają odpowiednio rzuty punktów
 na
płaszczyznę
na
płaszczyznę
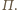 Dla punktu
Dla punktu
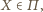 różnego od
różnego od
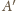 i
i
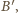 równość
równość
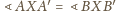 zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
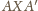 i
i
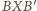 są podobne.
Równoważnie,
są podobne.
Równoważnie,
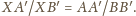 Jeśli
Jeśli
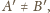 to
punkty
to
punkty
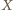 o żądanej własności tworzą okrąg Apoloniusza dla
punktów
o żądanej własności tworzą okrąg Apoloniusza dla
punktów
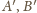 i stałej
i stałej
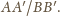 Jakie jest rozwiązanie, gdy
Jakie jest rozwiązanie, gdy
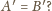 Czy możliwe, by
Czy możliwe, by
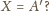
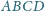 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku
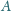 jest większa od
jest większa od
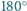 oraz zachodzi równość
oraz zachodzi równość
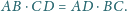 Punkt
Punkt
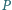 jest symetryczny do punktu
jest symetryczny do punktu
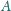 względem prostej
względem prostej
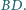 Udowodnij, że
Udowodnij, że
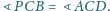
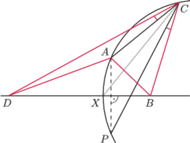
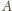 i
i
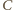 leżą na okręgu Apoloniusza dla punktów
leżą na okręgu Apoloniusza dla punktów
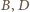 i stałej
i stałej
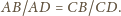 Z symetrii względem prostej
Z symetrii względem prostej
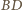 punkt
punkt
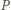 też na nim leży (
też na nim leży (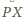 i
i
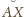 są równe, więc
są równe, więc
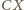 jest dwusieczną kąta
jest dwusieczną kąta
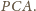 Jednocześnie
Jednocześnie
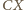 jest też dwusieczną kąta
jest też dwusieczną kąta
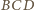 (własność z początku artykułu,
(własność z początku artykułu, 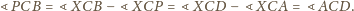
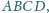 w którym
w którym
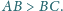 Na boku
Na boku
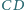 tego prostokąta skonstruuj takie punkty
tego prostokąta skonstruuj takie punkty
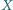 i
i
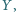 aby
aby
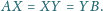
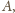 środka boku
środka boku
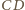 i stałej 2.
i stałej 2.
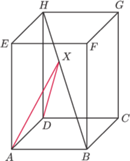
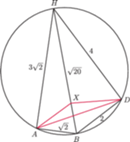
 o podstawach
o podstawach
 i
i
 będących kwadratami, przy czym
będących kwadratami, przy czym
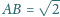 i
i
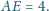 Punkt
Punkt
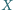 przesuwamy po przekątnej
przesuwamy po przekątnej
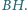 Znaleźć
minimalną wartość wyrażenia
Znaleźć
minimalną wartość wyrażenia
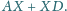
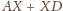 wynosi
wynosi
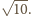
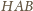 i
i
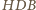 na jednej
płaszczyźnie, dostajemy czworokąt
na jednej
płaszczyźnie, dostajemy czworokąt
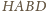 wpisany w okrąg.
wpisany w okrąg.
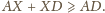 Równość zachodzi wtedy i tylko
wtedy, gdy
Równość zachodzi wtedy i tylko
wtedy, gdy
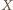 jest punktem przecięcia przekątnych tego czworokąta.
Szukana minimalna wartość wyrażenia
jest punktem przecięcia przekątnych tego czworokąta.
Szukana minimalna wartość wyrażenia
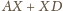 to długość
odcinka
to długość
odcinka
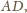 którą możemy obliczyć z twierdzenia Ptolemeusza:
którą możemy obliczyć z twierdzenia Ptolemeusza:
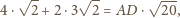
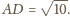
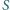 o środku w środku okręgu opisanego na trójkącie
o środku w środku okręgu opisanego na trójkącie
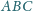 przecina krawędzie
przecina krawędzie
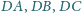 czworościanu
czworościanu
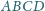 odpowiednio w punktach
odpowiednio w punktach
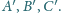 Płaszczyzny styczne
do tej sfery odpowiednio w punktach
Płaszczyzny styczne
do tej sfery odpowiednio w punktach
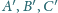 przecinają się w punkcie
przecinają się w punkcie
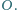 Wykazać, że punkt
Wykazać, że punkt
 jest środkiem sfery opisanej na
czworościanie
jest środkiem sfery opisanej na
czworościanie
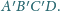
 i sfera
opisana na czworościanie
i sfera
opisana na czworościanie
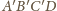 są prostopadłe. Zauważmy,
że
są prostopadłe. Zauważmy,
że
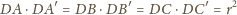
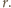 Rozważmy inwersję o środku
Rozważmy inwersję o środku
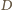 i promieniu
i promieniu
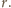 Zauważmy, że sfera
Zauważmy, że sfera
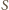 przechodzi na siebie, a punkty
przechodzi na siebie, a punkty
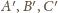 odpowiednio na
odpowiednio na
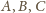 (i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
(i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
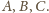 Jednakże środek sfery
Jednakże środek sfery
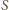 leży właśnie na
płaszczyźnie
leży właśnie na
płaszczyźnie
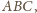 skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
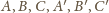 i sfera opisana na
czworościanie
i sfera opisana na
czworościanie
 też są prostopadłe.
też są prostopadłe.
 którego podstawą jest czworokąt wypukły
którego podstawą jest czworokąt wypukły
 o prostopadłych przekątnych
o prostopadłych przekątnych
 i
i
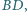 a rzutem
prostokątnym wierzchołka
a rzutem
prostokątnym wierzchołka
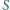 na podstawę jest punkt
na podstawę jest punkt
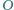 przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
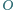 na
ściany boczne ostrosłupa leżą na jednym okręgu.
na
ściany boczne ostrosłupa leżą na jednym okręgu.
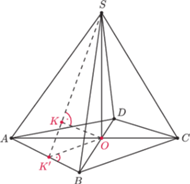
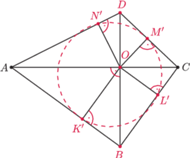
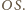 Weźmy rzut stereograficzny tej sfery z punktu
Weźmy rzut stereograficzny tej sfery z punktu
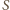 na
płaszczyznę
na
płaszczyznę
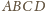 (
(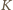 będzie rzutem prostokątnym
punktu
będzie rzutem prostokątnym
punktu
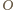 na ścianę
na ścianę
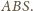 Płaszczyzna
Płaszczyzna
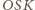 jest
prostopadła do krawędzi
jest
prostopadła do krawędzi
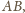 skąd wynika, że obraz
skąd wynika, że obraz
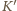 punktu
punktu
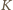 w tym przekształceniu będzie rzutem prostokątnym punktu
w tym przekształceniu będzie rzutem prostokątnym punktu
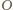 na krawędź
na krawędź
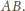 Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
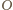 na pozostałe boki czworokąta
na pozostałe boki czworokąta
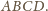 Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi –
Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi – 
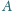 czworościanu
czworościanu
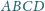 poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
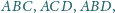 tworzą sześć równych kątów wtedy i tylko wtedy,
gdy
tworzą sześć równych kątów wtedy i tylko wtedy,
gdy

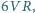 gdzie
gdzie
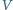 i
i
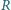 oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
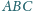 punkt
punkt
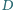 jest środkiem
przeciwprostokątnej
jest środkiem
przeciwprostokątnej
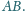 Dowieść, że prosta
Dowieść, że prosta
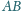 jest styczna do
okręgu, którego średnica łączy środki okręgów opisanych na trójkątach
jest styczna do
okręgu, którego średnica łączy środki okręgów opisanych na trójkątach
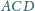 i
i
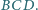

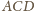 i
i
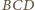 odpowiednio
przez
odpowiednio
przez
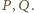 Niech
Niech
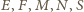 będą kolejno środkami
odcinków
będą kolejno środkami
odcinków
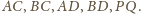 Proste
Proste
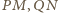 to symetralne
odcinków
to symetralne
odcinków
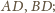 proste
proste
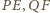 to symetralne odcinków
to symetralne odcinków
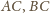 – przecinają się prostopadle w punkcie
– przecinają się prostopadle w punkcie
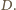 Okrąg
o średnicy
Okrąg
o średnicy
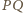 przechodzi więc przez punkt
przechodzi więc przez punkt
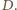 Ma on środek
w punkcie
Ma on środek
w punkcie
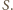
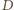 jest środkiem odcinka
jest środkiem odcinka
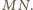 Zatem prosta
Zatem prosta
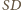 jest
równoległa do prostych
jest
równoległa do prostych
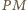 i
i
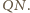 Prosta
Prosta
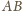 jest do nich
prostopadła. Wobec tego promień
jest do nich
prostopadła. Wobec tego promień
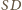 okręgu
okręgu
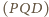 jest
prostopadły do
jest
prostopadły do
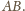 To znaczy, że ów okrąg jest styczny do prostej
To znaczy, że ów okrąg jest styczny do prostej
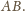
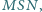 przy czym
przy czym
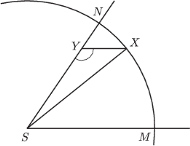
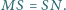 Punkt
Punkt
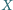 leży na krótszym łuku
leży na krótszym łuku
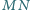 okręgu o środku
okręgu o środku
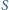 i promieniu
i promieniu
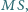 punkt
punkt
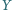 jest takim punktem odcinka
jest takim punktem odcinka
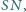 że proste
że proste
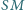 i
i
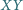 są równoległe. Znaleźć takie
położenie punktu
są równoległe. Znaleźć takie
położenie punktu
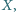 przy którym pole trójkąta
przy którym pole trójkąta
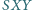 jest
największe.
jest
największe.
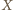 jest środkiem łuku
jest środkiem łuku
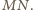
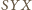 ma stałą miarę (niezależną od wyboru punktu
ma stałą miarę (niezależną od wyboru punktu
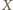 ),
a odcinek
),
a odcinek
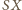 – stałą długość. Wszystkie rozważane trójkąty
– stałą długość. Wszystkie rozważane trójkąty
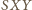 można więc wpisać w ten sam okrąg, przy czym kąt
można więc wpisać w ten sam okrąg, przy czym kąt
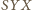 jest oparty na ustalonej cięciwie. Pole takiego trójkąta wynosi
jest oparty na ustalonej cięciwie. Pole takiego trójkąta wynosi
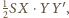 gdzie
gdzie
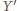 to rzut prostokątny punktu
to rzut prostokątny punktu
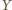 na
na
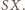 Jest ono największe, gdy
Jest ono największe, gdy
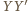 jest największe, czyli wtedy
i tylko wtedy, gdy
jest największe, czyli wtedy
i tylko wtedy, gdy
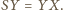 Ale to jest równoważne temu, że
Ale to jest równoważne temu, że
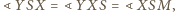 czyli temu, że
czyli temu, że
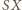 jest dwusieczną
kąta
jest dwusieczną
kąta
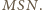
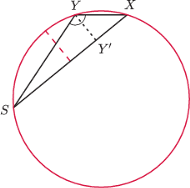
 kąt
kąt
 jest prosty. Wykaż, że
jest prosty. Wykaż, że

 symetrycznie względem prostych
symetrycznie względem prostych
 oraz
oraz
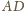 i przyjmijmy oznaczenia jak na rysunku.
Wówczas
i przyjmijmy oznaczenia jak na rysunku.
Wówczas
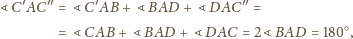
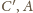 i
i
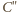 leżą, w tej właśnie kolejności, na
jednej prostej. Ponadto
leżą, w tej właśnie kolejności, na
jednej prostej. Ponadto
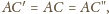 stąd
stąd
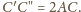
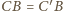 oraz
oraz
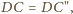 zatem
zatem
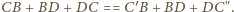 Teza wynika z faktu, że łamana
Teza wynika z faktu, że łamana
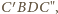 łącząca punkty
łącząca punkty
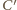 i
i
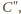 nie może być krótsza
niż odcinek
nie może być krótsza
niż odcinek
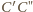 pomiędzy nimi:
pomiędzy nimi:
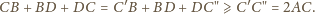
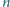 punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
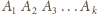 i że
i że
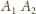 jest jej najdłuższym odcinkiem. Wtedy z
jest jej najdłuższym odcinkiem. Wtedy z
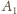 jest
bliżej do
jest
bliżej do
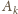 niż do
niż do
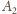 oraz z
oraz z
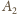 jest bliżej do
jest bliżej do
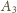 niż do
niż do
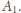 Zatem odcinek
Zatem odcinek
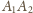 nie mógł zostać
narysowany!
nie mógł zostać
narysowany!
 punktów białych i
punktów białych i
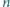 czarnych,
żadne trzy nie są współliniowe. Wykaż, że można je tak połączyć
czarnych,
żadne trzy nie są współliniowe. Wykaż, że można je tak połączyć
 odcinkami, by każdy odcinek miał końce różnych kolorów i by
żadne dwa odcinki nie miały punktów wspólnych.
odcinkami, by każdy odcinek miał końce różnych kolorów i by
żadne dwa odcinki nie miały punktów wspólnych.
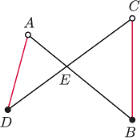
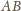 i
i
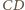 mają
wspólny punkt
mają
wspólny punkt
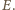 Wówczas
Wówczas
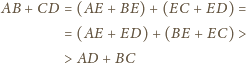
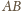 i
i
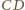 na
na
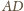 i
i
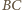 zmniejszyłaby sumę długości wszystkich
odcinków, sprzecznie z założeniem.
zmniejszyłaby sumę długości wszystkich
odcinków, sprzecznie z założeniem.