Zadanie ZM-1611
o zadaniu...
- Publikacja w Delcie: sierpień 2019
- Publikacja elektroniczna: 1 sierpnia 2019
Dana jest liczba całkowita 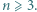 Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 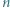 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 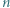 -kąta. Wykazać, że
-kąta. Wykazać, że 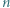 jest liczbą nieparzystą.
jest liczbą nieparzystą.

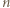 -kąta czadowym i zauważmy, że liczba czadowych trójkątów jest równa liczbie trójek kolorów. To oznacza, że jeśli warunki zadania są spełnione, to każda trójka kolorów pojawia się jako zbiór kolorów boków czadowego trójkąta dokładnie raz. W szczególności żaden czadowy trójkąt nie może mieć dwóch boków tego samego koloru.
-kąta czadowym i zauważmy, że liczba czadowych trójkątów jest równa liczbie trójek kolorów. To oznacza, że jeśli warunki zadania są spełnione, to każda trójka kolorów pojawia się jako zbiór kolorów boków czadowego trójkąta dokładnie raz. W szczególności żaden czadowy trójkąt nie może mieć dwóch boków tego samego koloru.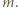 Z jednej strony liczba czadowych trójkątów o czerwonym boku jest równa
Z jednej strony liczba czadowych trójkątów o czerwonym boku jest równa 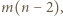 gdyż każdy czerwony odcinek jest bokiem dokładnie
gdyż każdy czerwony odcinek jest bokiem dokładnie 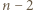 czadowych trójkątów. Z drugiej strony liczba ta jest równa liczbie sposobów doboru dwóch innych spośród
czadowych trójkątów. Z drugiej strony liczba ta jest równa liczbie sposobów doboru dwóch innych spośród  dostępnych kolorów do czerwonego, czyli
dostępnych kolorów do czerwonego, czyli 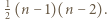 Stąd
Stąd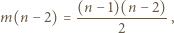
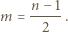
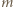 jest liczbą całkowitą, to
jest liczbą całkowitą, to 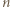 jest liczbą nieparzystą.
jest liczbą nieparzystą.