Składanie inwersji z symetrią»Zadanie 4
o zadaniu...
- Zadanie pochodzi z artykułu Składanie inwersji z symetrią
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (390 KB)
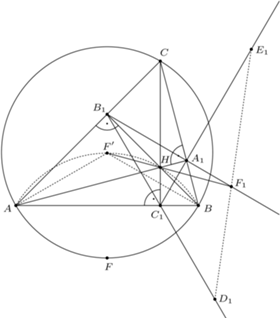
Trójkąt różnoboczny 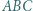 jest wpisany w okrąg
jest wpisany w okrąg 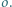 Punkty
Punkty 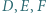 są środkami łuków
są środkami łuków 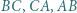 niezawierających pozostałych wierzchołków trójkąta. Punkty
niezawierających pozostałych wierzchołków trójkąta. Punkty 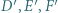 są symetryczne do punktów
są symetryczne do punktów 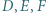 odpowiednio względem boków
odpowiednio względem boków 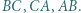 Wykazać, że punkty
Wykazać, że punkty 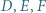 oraz ortocentrum trójkąta
oraz ortocentrum trójkąta 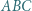 leżą na jednym okręgu.
leżą na jednym okręgu.

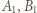 i
i 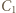 będą spodkami wysokości trójkąta
będą spodkami wysokości trójkąta 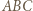 poprowadzonymi odpowiednio z wierzchołków
poprowadzonymi odpowiednio z wierzchołków 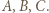 Ponieważ na czworokątach
Ponieważ na czworokątach 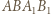 i
i 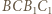 można opisać okręgi, to
można opisać okręgi, to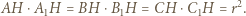
 i promieniu
i promieniu  złożoną z symetrią środkową względem punktu
złożoną z symetrią środkową względem punktu 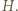 Obrazami punktów
Obrazami punktów 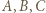 są zatem punkty
są zatem punkty 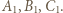 Ponieważ
Ponieważ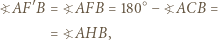
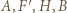 leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą
leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą 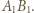 Obrazem punktu
Obrazem punktu 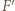 jest punkt
jest punkt 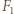 przecięcia prostych
przecięcia prostych 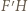 i
i 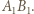 Analogicznie stwierdzamy, że w tym przekształceniu punkt
Analogicznie stwierdzamy, że w tym przekształceniu punkt 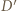 przechodzi na punkt
przechodzi na punkt 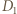 przecięcia prostych
przecięcia prostych 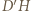 i
i 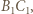 a punkt
a punkt 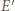 przechodzi na punkt
przechodzi na punkt 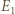 przecięcia prostych
przecięcia prostych 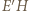 i
i 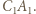
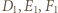 leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta
leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta 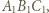 widzimy, że wystarczy wykazać, że
widzimy, że wystarczy wykazać, że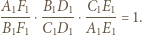
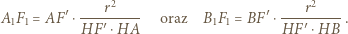
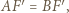 widzimy, że
widzimy, że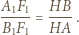

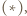 co kończy rozwiązanie.
co kończy rozwiązanie.