Zadanie ZM-1413
o zadaniu...
- Publikacja w Delcie: luty 2014
- Publikacja elektroniczna: 31-01-2014
Mając dane wektory
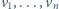 w przestrzeni, definiujemy zbiór
w przestrzeni, definiujemy zbiór
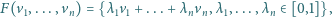
np.
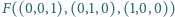 to standardowa kostka. Rozstrzygnąć,
czy dla pewnych wektorów można w ten sposób otrzymać ośmiościan
foremny.
to standardowa kostka. Rozstrzygnąć,
czy dla pewnych wektorów można w ten sposób otrzymać ośmiościan
foremny.
Uwaga. Zbiór
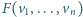 w geometrii wypukłej nazywa się sumą
Minkowskiego odcinków
w geometrii wypukłej nazywa się sumą
Minkowskiego odcinków
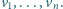
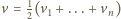 jest środkiem
symetrii zbioru
jest środkiem
symetrii zbioru
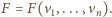 Istotnie, symetria
Istotnie, symetria
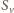 o środku
o środku
 przeprowadza wektor
przeprowadza wektor
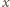 na
na
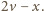 Dla dowolnego
Dla dowolnego
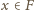 w postaci
w postaci
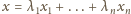 mamy
mamy
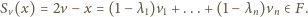
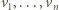 zbiór
zbiór
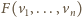 to ośmiościan foremny
to ośmiościan foremny
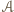 i że
i że
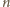 jest
najmniejsze możliwe (oczywiście
jest
najmniejsze możliwe (oczywiście
 ). Zauważmy, że wtedy
). Zauważmy, że wtedy
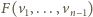 jest ścianą
jest ścianą
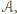 czyli trójkątem równobocznym,
który nie ma środka symetrii – sprzeczność.
czyli trójkątem równobocznym,
który nie ma środka symetrii – sprzeczność.
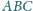 o ortocentrum
o ortocentrum
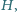 środku okręgu
opisanego
środku okręgu
opisanego
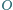 i kącie
i kącie
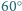 przy wierzchołku
przy wierzchołku
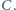 Udowodnić,
że dwusieczna kąta
Udowodnić,
że dwusieczna kąta
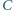 jest symetralną odcinka
jest symetralną odcinka
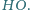
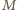 będzie środkiem boku
będzie środkiem boku
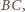 a
a
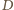 – spodkiem
wysokości z wierzchołka
– spodkiem
wysokości z wierzchołka
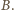 Ponieważ
Ponieważ
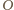 jest środkiem okręgu
opisanego, więc kąt
jest środkiem okręgu
opisanego, więc kąt
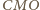 jest prosty oraz
jest prosty oraz
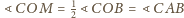 (kąt środkowy i wpisany). Oczywiście
(kąt środkowy i wpisany). Oczywiście
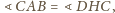 więc trójkąty
więc trójkąty
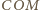 i
i
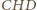 są podobne. Trójkąt
są podobne. Trójkąt
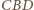 jest połową
trójkąta równobocznego, mamy więc
jest połową
trójkąta równobocznego, mamy więc
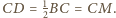 Stąd
trójkąty
Stąd
trójkąty
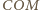 i
i
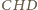 są przystające, a dokładniej jeden jest
obrazem drugiego w symetrii względem dwusiecznej kąta
są przystające, a dokładniej jeden jest
obrazem drugiego w symetrii względem dwusiecznej kąta
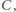 co daje
tezę.
co daje
tezę.
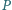 w jego
wnętrzu. Suma odległości punktu
w jego
wnętrzu. Suma odległości punktu
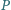 od krawędzi tego czworościanu jest
równa
od krawędzi tego czworościanu jest
równa
 Wykaż, że
Wykaż, że
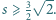
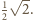
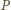 od dwóch przeciwległych krawędzi
czworościanu jest nie mniejsza od sumy odległości
od dwóch przeciwległych krawędzi
czworościanu jest nie mniejsza od sumy odległości
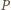 od zawierających
je przeciwległych ścian sześcianu, która z kolei jest większa lub równa
odległości pomiędzy takimi ścianami, czyli długości krawędzi sześcianu.
Czworościan ma trzy pary przeciwległych krawędzi, stąd
od zawierających
je przeciwległych ścian sześcianu, która z kolei jest większa lub równa
odległości pomiędzy takimi ścianami, czyli długości krawędzi sześcianu.
Czworościan ma trzy pary przeciwległych krawędzi, stąd
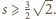
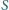 i
i
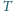 o następujących dwóch
własnościach:
o następujących dwóch
własnościach:
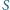 jest większa od objętości
czworościanu
jest większa od objętości
czworościanu
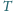 ;
;
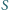 nie przekracza pola
żadnej ściany czworościanu
nie przekracza pola
żadnej ściany czworościanu
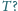
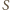 zbudujemy czworościan
zbudujemy czworościan
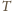 o żądanych własnościach. Niech
o żądanych własnościach. Niech
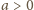 będzie taką liczbą, aby
liczba
będzie taką liczbą, aby
liczba
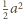 była większa od pola każdej ściany czworościanu
była większa od pola każdej ściany czworościanu
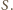 Niech
Niech
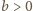 będzie taką liczbą, aby liczba
będzie taką liczbą, aby liczba
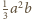 była
mniejsza od objętości czworościanu
była
mniejsza od objętości czworościanu
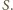
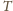 będzie czworościanem wpisanym w prostopadłościan
o podstawie
będzie czworościanem wpisanym w prostopadłościan
o podstawie
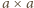 i wysokości
i wysokości
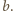 Objętość
Objętość
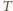 równa
jest
równa
jest
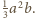 Każdą ścianę czworościanu
Każdą ścianę czworościanu
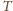 można
zrzutować na połowę podstawy prostopadłościanu, więc jej pole
przekracza
można
zrzutować na połowę podstawy prostopadłościanu, więc jej pole
przekracza
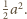 Z definicji liczb
Z definicji liczb
 i
i
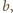 czworościany
czworościany
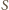 i
i
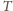 spełniają żądane warunki.
spełniają żądane warunki.
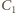 i
i
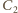 wpisane
odpowiednio w prostopadłościany o wymiarach
wpisane
odpowiednio w prostopadłościany o wymiarach
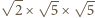 oraz
oraz
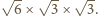
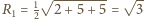 oraz
oraz
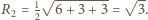
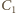 jest
trójkątem o bokach
jest
trójkątem o bokach
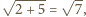
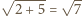 oraz
oraz
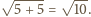 Wysokość takiego trójkąta, opuszczona na bok
o długości
Wysokość takiego trójkąta, opuszczona na bok
o długości
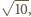 równa jest
równa jest
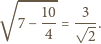
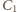 równe jest
równe jest
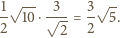
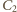 też równe jest
też równe jest
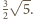
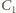 i
i
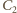 mają więc równe pola ścian
i promienie kul opisanych. Tymczasem ich objętości są różne:
mają więc równe pola ścian
i promienie kul opisanych. Tymczasem ich objętości są różne:
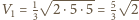 oraz
oraz
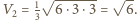
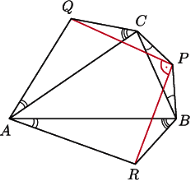
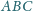 dane są punkty
dane są punkty
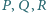 wyznaczone
przez warunki
wyznaczone
przez warunki
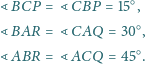
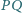 i
i
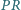 są równe i prostopadłe.
są równe i prostopadłe.
 będzie obrazem punktu
będzie obrazem punktu
 przy obrocie
przy obrocie
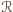 wokół
wokół
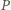 o
o
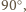 jak na rysunku. Wówczas
jak na rysunku. Wówczas
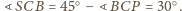 Ponadto, skoro
Ponadto, skoro
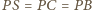 i
i
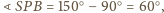 to trójkąt
to trójkąt
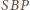 jest równoboczny. Zatem
jest równoboczny. Zatem
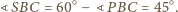
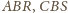 są podobne (kkk). Stąd
są podobne (kkk). Stąd
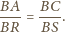
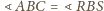 oznacza to, że trójkąty
oznacza to, że trójkąty
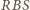 i
i
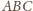 są podobne (bkb). Zatem
są podobne (bkb). Zatem
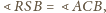 więc
również
więc
również
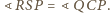 Ponadto
Ponadto
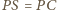 oraz
oraz
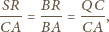
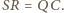 Tym samym trójkąty
Tym samym trójkąty
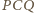 i
i
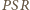 są
przystające (bkb). Z definicji punktu
są
przystające (bkb). Z definicji punktu
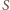 trójkąt
trójkąt
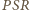 jest obrazem
trójkąta
jest obrazem
trójkąta
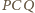 przy obrocie
przy obrocie
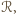 co kończy dowód.
co kończy dowód.
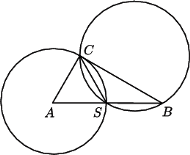
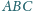 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku
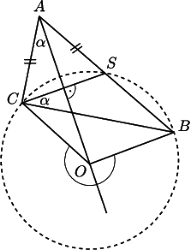
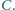 Okrąg o środku w punkcie
Okrąg o środku w punkcie
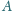 i promieniu
i promieniu
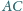 przecina
bok
przecina
bok
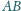 w punkcie
w punkcie
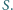 Udowodnić, że ten okrąg przystaje do
okręgu opisanego na trójkącie
Udowodnić, że ten okrąg przystaje do
okręgu opisanego na trójkącie
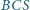 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
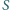 jest
środkiem
jest
środkiem
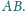
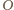 będzie środkiem okręgu opisanego na trójkącie
będzie środkiem okręgu opisanego na trójkącie
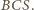 Ponieważ trójkąt
Ponieważ trójkąt
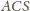 jest równoramienny, dwusieczna
kąta
jest równoramienny, dwusieczna
kąta
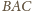 to symetralna odcinka
to symetralna odcinka
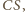 więc leży na niej punkt
więc leży na niej punkt
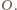 Oznaczmy
Oznaczmy
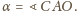 Wówczas
Wówczas
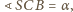 a skoro
a skoro
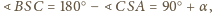 to
to
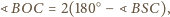
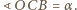 Równość
Równość
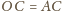 jest
równoważna
jest
równoważna
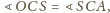 czyli
czyli
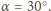 A to jest
równoważne temu, że
A to jest
równoważne temu, że
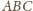 jest połówką trójkąta równobocznego
lub że
jest połówką trójkąta równobocznego
lub że
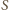 jest środkiem
jest środkiem
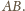

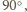 czyli trzeciemu kątowi.
czyli trzeciemu kątowi.

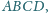 w którym
w którym

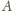 spełniają warunek
spełniają warunek
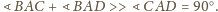 Z kolei rozważając kąt trójścienny
przy
Z kolei rozważając kąt trójścienny
przy
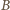 oraz trójkąty prostokątne
oraz trójkąty prostokątne
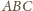 i
i
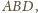 wnioskujemy,
że
wnioskujemy,
że
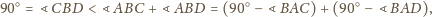
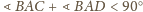 – sprzeczność.
– sprzeczność.
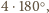 jako
suma kątów czterech trójkątów. Wobec tego istnieje taki wierzchołek
czworościanu, przy którym suma trzech kątów płaskich nie przekracza
jako
suma kątów czterech trójkątów. Wobec tego istnieje taki wierzchołek
czworościanu, przy którym suma trzech kątów płaskich nie przekracza
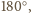 w przeciwnym razie suma wszystkich kątów płaskich czworościanu
przekraczałaby
w przeciwnym razie suma wszystkich kątów płaskich czworościanu
przekraczałaby
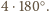
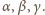 Wówczas
Wówczas
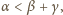 więc
więc
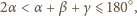
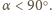 Analogicznie
Analogicznie
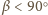 oraz
oraz
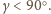
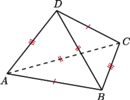
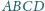 mamy
mamy
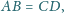
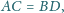
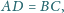 to wszystkie ściany czworościanu są
trójkątami ostrokątnymi.
to wszystkie ściany czworościanu są
trójkątami ostrokątnymi.
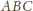 przez
przez
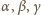 ; ich suma to
; ich suma to
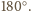 W każdym wierzchołku czworościanu
schodzą się takie właśnie trzy kąty płaskie. Stąd
W każdym wierzchołku czworościanu
schodzą się takie właśnie trzy kąty płaskie. Stąd
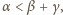 więc
więc
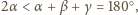 czyli
czyli
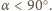 Analogicznie
Analogicznie
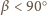 oraz
oraz
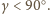
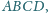 w którym
w którym
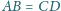 oraz
oraz
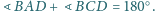 Udowodnij, że
Udowodnij, że
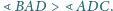

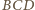 danego czworościanu wokół krawędzi
danego czworościanu wokół krawędzi
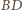 tak, aby znalazła się w płaszczyźnie ściany
tak, aby znalazła się w płaszczyźnie ściany
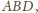 ale po
przeciwnej stronie prostej
ale po
przeciwnej stronie prostej
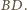 Na uzyskanym w ten sposób czworokącie
Na uzyskanym w ten sposób czworokącie
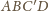 można opisać okrąg, gdyż
można opisać okrąg, gdyż
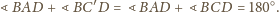
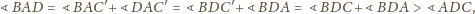
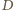 czworościanu. To kończy dowód.
czworościanu. To kończy dowód.
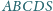 o podstawie
o podstawie
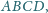 w którym
w którym
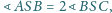
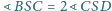 oraz
oraz
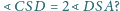

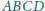 jest styczna do ściany
jest styczna do ściany
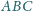 w punkcie
w punkcie
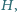 a sfera dopisana do tego czworościanu jest
styczna do ściany
a sfera dopisana do tego czworościanu jest
styczna do ściany
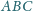 w punkcie
w punkcie
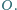 Dowieść, że jeżeli
Dowieść, że jeżeli
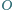 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
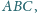 to
to
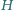 jest punktem przecięcia wysokości tego trójkąta.
jest punktem przecięcia wysokości tego trójkąta.
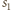 i
i
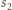 rozpatrywane sfery. Niech
rozpatrywane sfery. Niech
 będzie
stożkiem o wierzchołku
będzie
stożkiem o wierzchołku
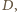 w który wpisane są sfery
w który wpisane są sfery
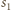 i
i
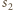 (każda tworząca stożka
(każda tworząca stożka
 jest wspólną styczną sfer
jest wspólną styczną sfer
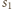 i
i
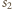 ).
Posługując się sferami Dandelina, wnioskujemy, że część wspólna
płaszczyzny
).
Posługując się sferami Dandelina, wnioskujemy, że część wspólna
płaszczyzny
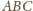 i stożka
i stożka
 jest elipsą wpisaną w trójkąt
jest elipsą wpisaną w trójkąt
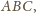 a punkty
a punkty
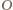 i
i
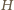 to jej ogniska. W takim razie
spełnione są równości
to jej ogniska. W takim razie
spełnione są równości
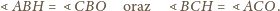
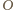 jest środkiem okręgu opisanego na
trójkącie
jest środkiem okręgu opisanego na
trójkącie
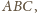 a
a
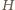 punktem przecięcia jego wysokości, to
powyższe równości są spełnione. Z drugiej strony dla danego punktu
punktem przecięcia jego wysokości, to
powyższe równości są spełnione. Z drugiej strony dla danego punktu
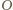 punkt
punkt
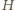 jest jednoznacznie wyznaczony przez powyższe
zależności. Skoro więc
jest jednoznacznie wyznaczony przez powyższe
zależności. Skoro więc
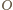 jest środkiem okręgu opisanego na
trójkącie
jest środkiem okręgu opisanego na
trójkącie
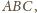 to
to
 musi być punktem przecięcia wysokości
tego trójkąta.
musi być punktem przecięcia wysokości
tego trójkąta.
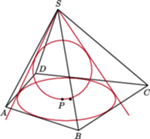
 o podstawie czworokąta
wypukłego
o podstawie czworokąta
wypukłego
 Sfera wpisana w ten ostrosłup jest styczna do ściany
Sfera wpisana w ten ostrosłup jest styczna do ściany
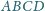 w punkcie
w punkcie
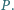 Dowieść, że
Dowieść, że
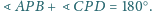
 będzie stożkiem o wierzchołku
będzie stożkiem o wierzchołku
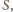 w który wpisana jest
sfera wpisana w ostrosłup
w który wpisana jest
sfera wpisana w ostrosłup
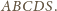 Część wspólna tego stożka
z płaszczyzną podstawy jest elipsą wpisaną w czworokąt
Część wspólna tego stożka
z płaszczyzną podstawy jest elipsą wpisaną w czworokąt
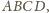 a punkt
a punkt
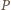 jest jej ogniskiem. Teza zadania jest po prostu jedną ze znanych
własności elipsy wpisanej w czworokąt.
jest jej ogniskiem. Teza zadania jest po prostu jedną ze znanych
własności elipsy wpisanej w czworokąt.
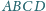 jest styczna do ścian
jest styczna do ścian
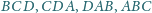 odpowiednio w punktach
odpowiednio w punktach
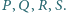 Odcinek
Odcinek
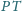 jest średnicą tej sfery, a punkty
jest średnicą tej sfery, a punkty
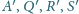 są punktami
przecięcia prostych
są punktami
przecięcia prostych
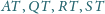 z płaszczyzną
z płaszczyzną
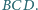 Dowieść,
że punkt
Dowieść,
że punkt
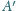 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
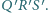
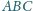 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków
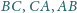 odpowiednio w punktach
odpowiednio w punktach
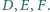 Punkty
Punkty
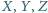 zostały obrane odpowiednio na bokach
zostały obrane odpowiednio na bokach
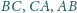 tak,
że
tak,
że
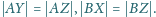 Dowieść, że prosta
Dowieść, że prosta
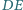 połowi
odcinek
połowi
odcinek

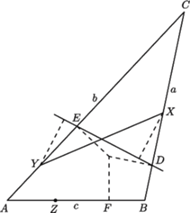
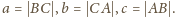 Równości
Równości
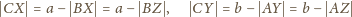
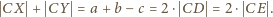
 i
i
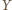 leżą po przeciwnych stronach
prostej
leżą po przeciwnych stronach
prostej
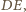 w jednakowych odległościach od odpowiednich końców
odcinka
w jednakowych odległościach od odpowiednich końców
odcinka
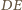 :
:
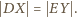
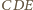 oznacza to z kolei, że
punkty
oznacza to z kolei, że
punkty
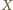 i
i
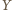 leżą w jednakowych odległościach od prostej
leżą w jednakowych odległościach od prostej
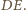 Stąd już wynika, że ta prosta przechodzi przez środek odcinka
Stąd już wynika, że ta prosta przechodzi przez środek odcinka
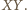
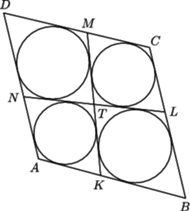
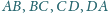 czworokąta wypukłego
czworokąta wypukłego
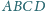 dane są
odpowiednio punkty
dane są
odpowiednio punkty
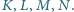 Odcinki
Odcinki
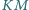 i
i
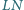 przecinają
się w punkcie
przecinają
się w punkcie
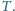 Udowodnić, że jeśli w każdy z czworokątów
Udowodnić, że jeśli w każdy z czworokątów
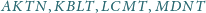 można wpisać okrąg, to w czworokąt
można wpisać okrąg, to w czworokąt
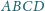 także.
także.
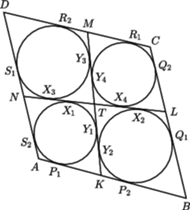
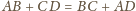 jest
równoważny
jest
równoważny
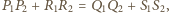 gdyż
gdyż
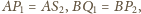
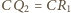 i
i
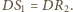 Zauważmy, że
Zauważmy, że
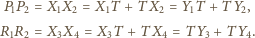
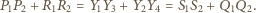
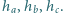 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
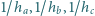 można zbudować
trójkąt.
można zbudować
trójkąt.
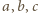 tak, by pole było
równe
tak, by pole było
równe
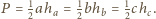 Korzystając z nierówności
Korzystając z nierówności
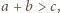 uzyskujemy wtedy
uzyskujemy wtedy
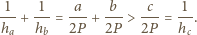
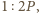 ma bowiem boki
długości
ma bowiem boki
długości
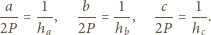
 i
i
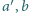 i
i
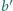 oraz
oraz
 i
i
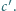 Wykaż, że
z odcinków o długościach
Wykaż, że
z odcinków o długościach
 można zbudować
trójkąt.
można zbudować
trójkąt.

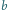
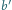

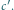

 danego czworościanu
i zawierające ją ściany. Obróćmy wokół niej jedną z tych ścian tak, aby
znalazła się w tej samej płaszczyźnie, co druga, ale po przeciwnej stronie tej
krawędzi.
danego czworościanu
i zawierające ją ściany. Obróćmy wokół niej jedną z tych ścian tak, aby
znalazła się w tej samej płaszczyźnie, co druga, ale po przeciwnej stronie tej
krawędzi.
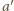 ; oznaczmy drugą przez
; oznaczmy drugą przez
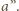 W wyjściowym czworościanie odcinek
W wyjściowym czworościanie odcinek
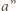 odpowiada
łamanej łączącej końce krawędzi
odpowiada
łamanej łączącej końce krawędzi
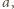 więc z nierówności trójkąta
więc z nierówności trójkąta
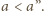
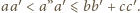 Analogicznie
dowodzimy pozostałych dwóch nierówności trójkąta dla odcinków
o długościach
Analogicznie
dowodzimy pozostałych dwóch nierówności trójkąta dla odcinków
o długościach
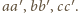
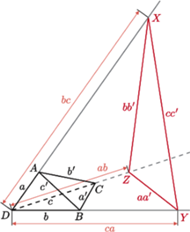
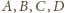 ; z uwagi
na przemienność iloczynów
; z uwagi
na przemienność iloczynów
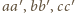 możemy przyjąć,
że
możemy przyjąć,
że
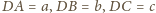 (
(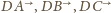 wybierzmy takie punkty odpowiednio
wybierzmy takie punkty odpowiednio
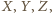 aby
aby
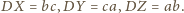 Punkty
Punkty
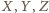 nie są współliniowe,
ponieważ rozważane półproste nie leżą w jednej płaszczyźnie.
nie są współliniowe,
ponieważ rozważane półproste nie leżą w jednej płaszczyźnie.
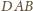 i
i
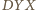 są podobne, bo mają wspólny kąt przy
wierzchołku
są podobne, bo mają wspólny kąt przy
wierzchołku
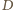 oraz
oraz
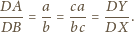
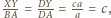 czyli
czyli
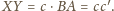
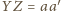 oraz
oraz
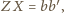 więc
trójkąt
więc
trójkąt
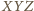 ma boki o żądanych długościach.
ma boki o żądanych długościach.
 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
 można zbudować
trójkąt.
można zbudować
trójkąt.
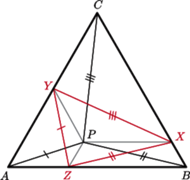
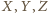 będą takimi punktami odpowiednio na bokach
będą takimi punktami odpowiednio na bokach
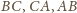 trójkąta
trójkąta
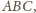 że
że
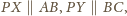
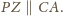 Wówczas trapezy
Wówczas trapezy
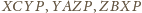 są
równoramienne (bo ich kąty to
są
równoramienne (bo ich kąty to
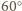 i
i
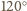 ). Wobec tego
). Wobec tego
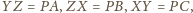 więc trójkąt
więc trójkąt
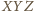 jest zbudowany
z odcinków o żądanych długościach.
jest zbudowany
z odcinków o żądanych długościach.

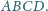 Ramiona
Ramiona
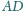 i
i
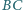 przecinają się
w punkcie
przecinają się
w punkcie
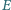 i są średnicami okręgów stycznych zewnętrznie
w punkcie
i są średnicami okręgów stycznych zewnętrznie
w punkcie
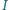 . Udowodnić, że
. Udowodnić, że
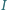 leży na dwusiecznej kąta
leży na dwusiecznej kąta
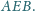

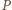 i
i
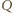 będą odpowiednio środkami ramion
będą odpowiednio środkami ramion
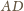 i
i
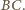 Połączmy je odcinkiem. Jest on równoległy do podstawy
Połączmy je odcinkiem. Jest on równoległy do podstawy
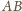 i
zawiera punkt
i
zawiera punkt
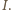 Dlatego
Dlatego
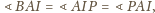 więc
więc
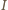 leży na dwusiecznej kąta
leży na dwusiecznej kąta
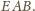 Analogicznie
Analogicznie
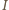 leży na
dwusiecznej kąta
leży na
dwusiecznej kąta
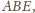 więc przechodzi przez niego także trzecia
dwusieczna trójkąta
więc przechodzi przez niego także trzecia
dwusieczna trójkąta
 leży wewnątrz czworościanu
leży wewnątrz czworościanu
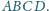 Przez każdą
krawędź tego czworościanu prowadzimy płaszczyznę równoległą do prostej
łączącej punkt
Przez każdą
krawędź tego czworościanu prowadzimy płaszczyznę równoległą do prostej
łączącej punkt
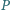 ze środkiem przeciwległej krawędzi. Wykazać, że
istnieje punkt wspólny otrzymanych sześciu płaszczyzn.
ze środkiem przeciwległej krawędzi. Wykazać, że
istnieje punkt wspólny otrzymanych sześciu płaszczyzn.
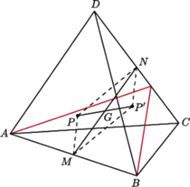
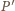 punktu
punktu
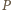 względem
środka ciężkości
względem
środka ciężkości
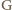 danego czworościanu należy do każdej
z sześciu rozważanych płaszczyzn. Wystarczy, że udowodnimy, iż punkt
danego czworościanu należy do każdej
z sześciu rozważanych płaszczyzn. Wystarczy, że udowodnimy, iż punkt
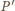 należy do płaszczyzny
należy do płaszczyzny
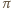 przechodzącej przez punkty
przechodzącej przez punkty
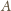 i
i
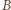 oraz równoległej do prostej łączącej punkt
oraz równoległej do prostej łączącej punkt
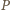 ze
środkiem krawędzi
ze
środkiem krawędzi
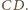
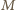 i
i
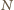 będą środkami krawędzi
będą środkami krawędzi
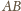 i
i
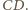 Punkt
Punkt
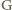 jest środkiem odcinka
jest środkiem odcinka
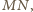 a więc czworokąt
a więc czworokąt
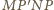 jest
równoległobokiem. Zatem proste
jest
równoległobokiem. Zatem proste
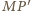 i
i
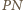 są równoległe. Skoro
punkt
są równoległe. Skoro
punkt
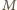 leży w płaszczyźnie
leży w płaszczyźnie
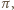 to prosta
to prosta
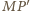 także.
To dowodzi, że punkt
także.
To dowodzi, że punkt
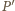 należy do płaszczyzny
należy do płaszczyzny
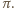
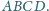 Odcinki
Odcinki
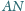 i
i
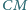 są
dwusiecznymi w trójkącie
są
dwusiecznymi w trójkącie
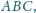 odcinek
odcinek
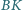 jest dwusieczną
w trójkącie
jest dwusieczną
w trójkącie
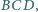 zaś odcinek
zaś odcinek
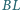 jest dwusieczną
w trójkącie
jest dwusieczną
w trójkącie
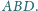 Wykazać, że istnieje punkt wspólny płaszczyzn
Wykazać, że istnieje punkt wspólny płaszczyzn