Nic nie może przecież wiecznie trwać»Zadanie 1
o zadaniu...
- Zadanie pochodzi z artykułu Nic nie może przecież wiecznie trwać
- Publikacja w Delcie: sierpień 2020
- Publikacja elektroniczna: 1 sierpnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (379 KB)
Na okręgu znajduje się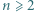 
punktów czarnych i 
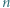białych. Rysujemy 
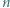cięciw, z których każda ma jeden koniec biały a drugi czarny. Udowodnić, że można zrobić to tak, by każde dwie narysowane cięciwy przecinały się.
Wskazówka
Narysować 
cięciw "byle jak" i zastosować rozumowanie podobne do tego, które przedstawiono we wstępie.