Pokażemy, że gdy 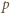 jest nieparzystą liczbą pierwszą, równanie
jest nieparzystą liczbą pierwszą, równanie 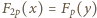 nie ma rozwiązań w liczbach całkowitych dodatnich.
nie ma rozwiązań w liczbach całkowitych dodatnich.
Przypuśćmy, że para liczb całkowitych 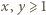 jest rozwiązaniem. Zgodnie z małym twierdzeniem Fermata,
jest rozwiązaniem. Zgodnie z małym twierdzeniem Fermata,
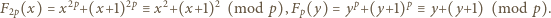
Jeśli więc 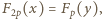 to
to 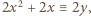 czyli
czyli 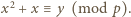
Z wypukłości funkcji 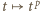 (w zbiorze liczb dodatnich) wynika nierówność
(w zbiorze liczb dodatnich) wynika nierówność
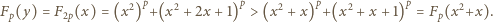
Funkcja 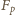 jest rosnąca; stąd
jest rosnąca; stąd 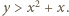 Skoro zaś
Skoro zaś 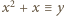 (mod
(mod 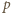 ), widzimy, że
), widzimy, że 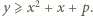 A zatem
A zatem 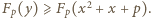 Aby uzyskać oczekiwaną sprzeczność, wystarczy wykazać, że
Aby uzyskać oczekiwaną sprzeczność, wystarczy wykazać, że
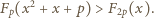 |
(1) |
Oznaczmy: 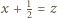 ; wtedy
; wtedy 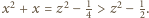 Ponownie korzystając z wypukłości funkcji
Ponownie korzystając z wypukłości funkcji 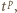 mamy nierówność
mamy nierówność 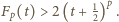 Wobec tego
Wobec tego
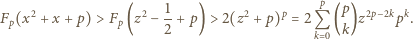 |
(2) |
Z drugiej strony,
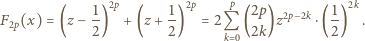 |
(3) |
Nierówność (1) będzie udowodniona, jeśli pokażemy, że w wyrażeniu po prawej stronie (2) współczynnik stojący przy 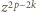 jest nie mniejszy niż analogiczny współczynnik w wyrażeniu (3); czyli, że
jest nie mniejszy niż analogiczny współczynnik w wyrażeniu (3); czyli, że
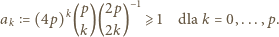 |
(4) |
Łatwo przerachować, że
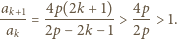
Stąd 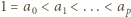 ; oszacowanie (4) gotowe, dowód zakończony.
; oszacowanie (4) gotowe, dowód zakończony.

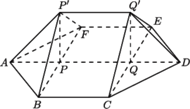
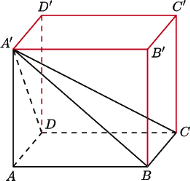
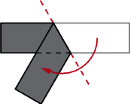
 W wierzchołku
W wierzchołku  podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż
podstawy siedzi pająk. Chce on przejść po powierzchni bocznej, odwiedzając wszystkie krawędzie boczne (być może w ich końcach) i wrócić do punktu wyjścia. Z rysunku i z nierówności trójkąta wynika, że istnieje droga krótsza niż 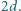

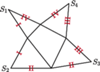
 z
z 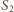 sklejają się w innym punkcie, niż
sklejają się w innym punkcie, niż 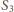 z
z 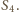 Wynika to z faktu, że na rysunku wysokości trójkątów, poprowadzone z wierzchołków
Wynika to z faktu, że na rysunku wysokości trójkątów, poprowadzone z wierzchołków 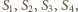 nie przecinają się w jednym punkcie - spodku wysokości ostrosłupa - a powinny.
nie przecinają się w jednym punkcie - spodku wysokości ostrosłupa - a powinny.
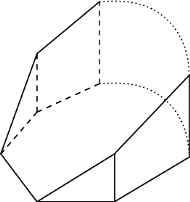
 o wszystkich bokach równej długości i kątach przy wierzchołkach
o wszystkich bokach równej długości i kątach przy wierzchołkach  równych odpowiednio:
równych odpowiednio: 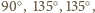
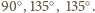 Niech
Niech 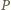 będzie punktem przecięcia przekątnych
będzie punktem przecięcia przekątnych 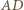 oraz
oraz 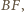 a
a 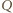 punktem przecięcia przekątnych
punktem przecięcia przekątnych 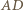 oraz
oraz 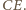 (
(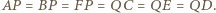 Wybierzmy teraz w przestrzeni punkty
Wybierzmy teraz w przestrzeni punkty 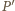 oraz
oraz 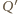 po tej samej stronie płaszczyzny sześciokąta, tak aby proste
po tej samej stronie płaszczyzny sześciokąta, tak aby proste 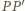 i
i 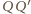 były prostopadłe do tej płaszczyzny oraz aby
były prostopadłe do tej płaszczyzny oraz aby  Wielościan
Wielościan  (
(
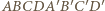 będzie prostopadłościanem. Wówczas ostrosłup
będzie prostopadłościanem. Wówczas ostrosłup 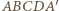 spełnia warunki zadania.
spełnia warunki zadania.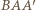 oraz
oraz 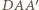 są, oczywiście, prostokątne. Ponadto, ponieważ prosta
są, oczywiście, prostokątne. Ponadto, ponieważ prosta 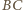 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 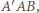 to jest ona prostopadła do każdej prostej z tej płaszczyzny, w szczególności do prostej
to jest ona prostopadła do każdej prostej z tej płaszczyzny, w szczególności do prostej 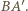 Zatem trójkąt
Zatem trójkąt 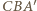 jest prostokątny. Podobnie dowodzimy, że trójkąt
jest prostokątny. Podobnie dowodzimy, że trójkąt 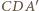 jest prostokątny.
jest prostokątny.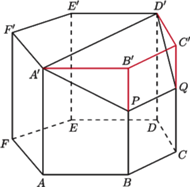
 oraz
oraz  Graniastosłup ten ma 18 krawędzi i wszystkie jego ściany mają parzystą liczbę boków. Gdyby udało się dodać jedną krawędź, nie zmieniając własności ścian, to otrzymany wielościan spełniałby warunki zadania. Zauważmy, że sześciokąt
Graniastosłup ten ma 18 krawędzi i wszystkie jego ściany mają parzystą liczbę boków. Gdyby udało się dodać jedną krawędź, nie zmieniając własności ścian, to otrzymany wielościan spełniałby warunki zadania. Zauważmy, że sześciokąt  można bez trudu podzielić jedną z przekątnych na dwa czworokąty. Teraz tylko trzeba zrobić z tych czworokątów ściany wielościanu przez pochylenie jednego z nich. Poprowadźmy więc przez punkty
można bez trudu podzielić jedną z przekątnych na dwa czworokąty. Teraz tylko trzeba zrobić z tych czworokątów ściany wielościanu przez pochylenie jednego z nich. Poprowadźmy więc przez punkty 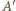 oraz
oraz 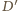 płaszczyznę przecinającą krawędzie
płaszczyznę przecinającą krawędzie 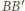 i
i 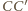 odpowiednio w punktach
odpowiednio w punktach 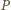 oraz
oraz 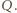 Płaszczyzna ta dzieli graniastosłup na dwa wielościany, z których jeden spełnia warunki zadania: ma osiem ścian będących czworokątami i jedną ścianę sześciokątną. Ponadto wielościan ten ma
Płaszczyzna ta dzieli graniastosłup na dwa wielościany, z których jeden spełnia warunki zadania: ma osiem ścian będących czworokątami i jedną ścianę sześciokątną. Ponadto wielościan ten ma 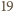 krawędzi.
krawędzi.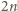 -kątem, dla
-kątem, dla 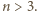
 W turnieju, w którym bierze udział
W turnieju, w którym bierze udział 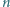 drużyn, zostanie rozegranych
drużyn, zostanie rozegranych 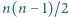 meczów każdy z każdym. Wykazać, że możliwe jest takie podzielenie rozgrywek na
meczów każdy z każdym. Wykazać, że możliwe jest takie podzielenie rozgrywek na  rund, by każda drużyna wystąpiła w każdej rundzie dokładnie raz.
rund, by każda drużyna wystąpiła w każdej rundzie dokładnie raz.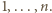 Niech w
Niech w 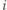 -tej rundzie (dla
-tej rundzie (dla 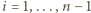 ) drużyny
) drużyny 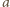 i
i 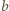 (dla
(dla 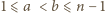 ) grają ze sobą, jeśli
) grają ze sobą, jeśli 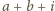 jest podzielne przez
jest podzielne przez 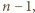 zaś drużyny
zaś drużyny 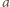 i
i 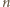 (dla
(dla 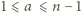 ) - jeśli
) - jeśli 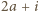 jest podzielne przez
jest podzielne przez 
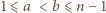 dokładnie jedna spośród
dokładnie jedna spośród 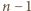 kolejnych liczb
kolejnych liczb 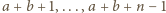 jest podzielna przez
jest podzielna przez 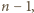 więc
więc  i
i 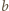 zagrają ze sobą w dokładnie jednej z rund. Podobnie drużyny
zagrają ze sobą w dokładnie jednej z rund. Podobnie drużyny 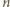 i
i 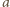 dla
dla 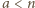 zagrają ze sobą dokładnie raz, ponieważ dokładnie jedna z liczb
zagrają ze sobą dokładnie raz, ponieważ dokładnie jedna z liczb 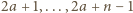 jest podzielna przez
jest podzielna przez 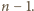
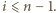 Gdyby drużyna
Gdyby drużyna  grała w
grała w 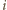 -tej rundzie dwa razy, to dla pewnych
-tej rundzie dwa razy, to dla pewnych  liczba
liczba 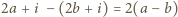 byłaby podzielna przez
byłaby podzielna przez  Ponieważ
Ponieważ  jest parzyste, dostalibyśmy, że
jest parzyste, dostalibyśmy, że  co jest niemożliwe. Gdyby drużyna
co jest niemożliwe. Gdyby drużyna  grała dwa razy w
grała dwa razy w 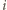 -tej rundzie, to zachodziłaby jedna z dwóch możliwości: 1) drużyna
-tej rundzie, to zachodziłaby jedna z dwóch możliwości: 1) drużyna  gra z drużynami
gra z drużynami 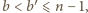 skąd
skąd 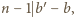 a to jest niemożliwe; 2) drużyna
a to jest niemożliwe; 2) drużyna  gra z drużynami
gra z drużynami  i
i  skąd
skąd 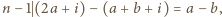 co również jest niemożliwe.
co również jest niemożliwe.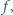 odwzorowująca zbiór liczb całkowitych dodatnich w siebie, jest niemalejąca i spełnia równość
odwzorowująca zbiór liczb całkowitych dodatnich w siebie, jest niemalejąca i spełnia równość 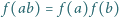 dla dowolnych liczb względnie pierwszych
dla dowolnych liczb względnie pierwszych 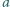 i
i 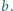 Udowodnić, że
Udowodnić, że
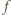 wynika prawdziwość dwóch nierówności:
wynika prawdziwość dwóch nierówności: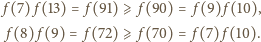
 ] wykazał, że funkcja
] wykazał, że funkcja 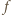 spełniająca podane warunki musi być postaci
spełniająca podane warunki musi być postaci 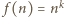 dla pewnego
dla pewnego 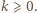
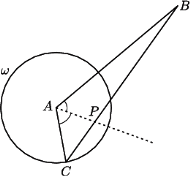
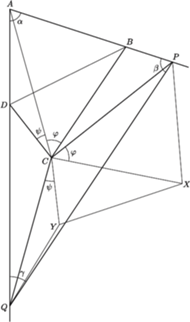
 oraz okrąg
oraz okrąg  o środku w punkcie
o środku w punkcie 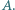 Dla punktu
Dla punktu 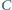 należącego do okręgu
należącego do okręgu 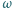 i nienależącego do prostej
i nienależącego do prostej 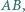 punkt
punkt 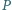 jest przecięciem prostej
jest przecięciem prostej 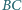 i dwusiecznej kąta
i dwusiecznej kąta 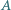 w trójkącie
w trójkącie 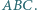 Wyznaczyć zbiór wszystkich otrzymanych w ten sposób punktów
Wyznaczyć zbiór wszystkich otrzymanych w ten sposób punktów 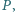 gdy
gdy 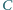 przebiega okrąg
przebiega okrąg 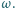

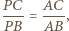 a skąd
a skąd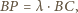
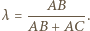
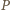 to obraz punktu
to obraz punktu 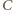 przy jednokładności o środku
przy jednokładności o środku 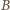 i skali
i skali 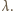 Poszukiwany zbiór punktów
Poszukiwany zbiór punktów 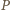 jest więc obrazem okręgu
jest więc obrazem okręgu 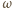 (bez dwóch punktów) przy tej jednokładności.
(bez dwóch punktów) przy tej jednokładności.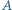 oraz najmniejszą liczbę
oraz najmniejszą liczbę 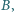 takie że dla każdej czwórki liczb rzeczywistych
takie że dla każdej czwórki liczb rzeczywistych 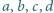 spełniona jest nierówność
spełniona jest nierówność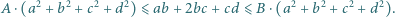
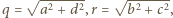
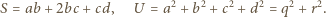
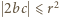 oraz
oraz 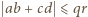 (nier. Cauchy'ego-Schwarza), zatem
(nier. Cauchy'ego-Schwarza), zatem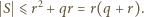
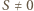 (więc
(więc 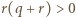 ). Wówczas
). Wówczas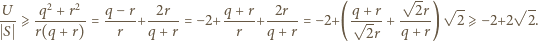
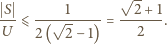
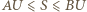 zachodzi ze stałymi
zachodzi ze stałymi 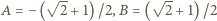 (dla
(dla  oczywiście też).
oczywiście też).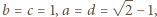 uzyskujemy równość
uzyskujemy równość 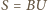 (z podaną stałą
(z podaną stałą 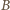 ); zaś zmieniając znak w
); zaś zmieniając znak w  i
i 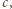 dostajemy równość
dostajemy równość 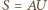 (z podaną stałą
(z podaną stałą 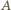 ). Znalezione stałe są więc optymalne.
). Znalezione stałe są więc optymalne. w którym kąty wewnętrzne przy wierzchołkach
w którym kąty wewnętrzne przy wierzchołkach 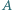 oraz
oraz 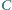 są równe, przy tym ostre. Punkty
są równe, przy tym ostre. Punkty 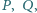 leżące odpowiednio na półprostych
leżące odpowiednio na półprostych 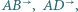 są wyznaczone przez warunki
są wyznaczone przez warunki 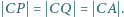 Wykazać, że długość odcinka
Wykazać, że długość odcinka  nie przekracza obwodu trójkąta
nie przekracza obwodu trójkąta 
 leży wewnątrz trójkąta
leży wewnątrz trójkąta 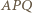 (jest to bowiem środek okręgu opisanego na tym trójkącie, leżący w obrębie kąta ostrego
(jest to bowiem środek okręgu opisanego na tym trójkącie, leżący w obrębie kąta ostrego 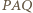 ). Oznaczmy kąty tego trójkąta:
). Oznaczmy kąty tego trójkąta: 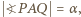
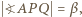
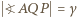 ; ponadto niech
; ponadto niech 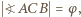
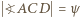 ; z założenia
; z założenia 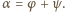
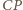 i
i  czworokąta (wklęsłego)
czworokąta (wklęsłego) 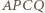 budujemy, po zewnętrznej jego stronie, trójkąty
budujemy, po zewnętrznej jego stronie, trójkąty 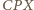 i
i 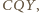 przystające odpowiednio do trójkątów
przystające odpowiednio do trójkątów 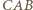 i
i 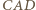 :
: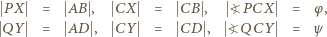
 leży między
leży między 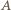 i
i 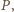 zaś
zaś 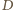 między
między 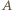 i
i 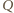 ; ale przy innym uporządkowaniu punktów, na jednej lub drugiej z tych prostych, rozumowanie nie wymaga żadnych zmian). Skoro
; ale przy innym uporządkowaniu punktów, na jednej lub drugiej z tych prostych, rozumowanie nie wymaga żadnych zmian). Skoro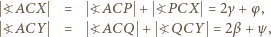
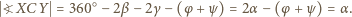
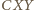 jest przystający do trójkąta
jest przystający do trójkąta 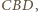 wobec czego
wobec czego 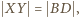 i otrzymujemy tezę zadania:
i otrzymujemy tezę zadania: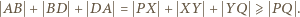

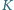 ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (
ma środek w środku kwadratu i jest styczne zewnętrznie do każdego z pozostałych kół (
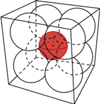
 dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 (
dla sześcianu o krawędzi 2 i ośmiu kul o średnicy 1 ( -wymiarowej kuli
-wymiarowej kuli 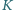 dla
dla  -wymiarowego hipersześcianu o krawędzi 2 i
-wymiarowego hipersześcianu o krawędzi 2 i 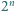 kul
kul 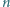 -wymiarowych o średnicy 1.
-wymiarowych o średnicy 1.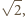 stąd
stąd 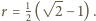
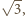 stąd
stąd 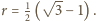
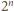 kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość
kul równa jest 1, a przekątna hipersześcianu jednostkowego ma długość 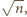 stąd
stąd 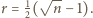
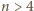 uzyskujemy
uzyskujemy 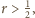 więc "mała" kulka
więc "mała" kulka 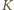 jest większa od każdej z "dużych" kul, a dla
jest większa od każdej z "dużych" kul, a dla 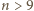 mamy
mamy 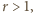 czyli kula
czyli kula 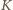 wystaje poza hipersześcian!
wystaje poza hipersześcian!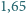 m. Czy istnieje możliwość przesłania fletu?
m. Czy istnieje możliwość przesłania fletu?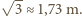



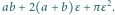
 -otoczkę pudełka o wymiarach
-otoczkę pudełka o wymiarach 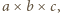 czyli zbiór złożony z wszystkich punktów z jego wnętrza oraz punktów odległych od niego o mniej niż
czyli zbiór złożony z wszystkich punktów z jego wnętrza oraz punktów odległych od niego o mniej niż 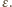 Ma ona kształt większego prostopadłościanu o zaokrąglonych krawędziach i rogach. Jej objętość równa jest
Ma ona kształt większego prostopadłościanu o zaokrąglonych krawędziach i rogach. Jej objętość równa jest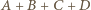
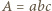 (objętość wyjściowego prostopadłościanu),
(objętość wyjściowego prostopadłościanu),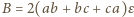 (objętości prostopadłościanów zbudowanych na ścianach),
(objętości prostopadłościanów zbudowanych na ścianach),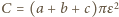 (fragmenty na równoległych krawędziach sumują się do walców o promieniu podstawy
(fragmenty na równoległych krawędziach sumują się do walców o promieniu podstawy  ),
),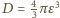 (fragmenty na rogach prostopadłościanu sumują się do kuli o promieniu
(fragmenty na rogach prostopadłościanu sumują się do kuli o promieniu  ).
).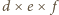 da się włożyć do pudełka o wymiarach
da się włożyć do pudełka o wymiarach 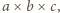 to również
to również  -otoczka pierwszego mieści się w
-otoczka pierwszego mieści się w  -otoczce drugiego. To z kolei oznacza, że różnica objętości jest nieujemna:
-otoczce drugiego. To z kolei oznacza, że różnica objętości jest nieujemna: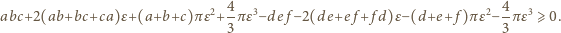
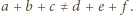
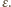 Skoro ma on wartość nieujemną dla każdego
Skoro ma on wartość nieujemną dla każdego 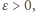 to musi mieć dodatni współczynnik przy najwyższej potędze
to musi mieć dodatni współczynnik przy najwyższej potędze 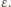 Stąd
Stąd 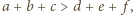 co kończy dowód.
co kończy dowód.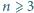 można wybrać
można wybrać 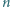 punktów na płaszczyźnie tak, aby odległość między każdymi dwoma była co najwyżej
punktów na płaszczyźnie tak, aby odległość między każdymi dwoma była co najwyżej 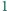 i była równa
i była równa 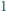 dla dokładnie
dla dokładnie 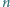 par punktów.
par punktów.
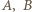 i
i 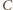 leżące w wierzchołkach trójkąta równobocznego o boku
leżące w wierzchołkach trójkąta równobocznego o boku 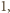 a pozostałe
a pozostałe 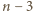 punkty z krótszego łuku
punkty z krótszego łuku 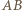 okręgu o środku
okręgu o środku 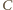 i promieniu
i promieniu 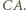
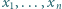 będą liczbami rzeczywistymi dodatnimi, przy czym
będą liczbami rzeczywistymi dodatnimi, przy czym 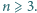 Dla wygody przyjmijmy dodatkowo, że
Dla wygody przyjmijmy dodatkowo, że 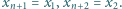
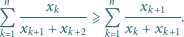
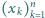 jest monotoniczny, to
jest monotoniczny, to
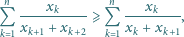
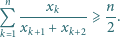
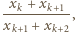 dla
dla 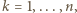 wynosi
wynosi 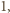 to korzystając z nierówności między średnimi, dostajemy
to korzystając z nierówności między średnimi, dostajemy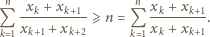
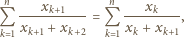
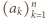 i
i 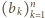 spełniają
spełniają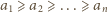
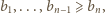
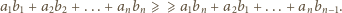
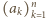 i
i 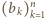 spełniają
spełniają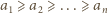
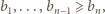
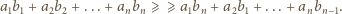
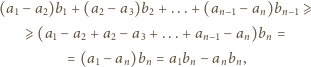
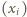 jest nierosnący:
jest nierosnący: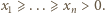
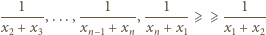
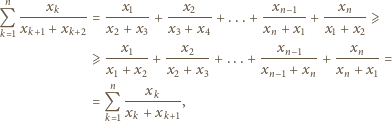
 jest niemalejący, postępujemy analogicznie.
jest niemalejący, postępujemy analogicznie.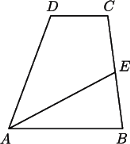
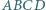 boki
boki 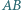 i
i 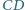 są równoległe oraz
są równoległe oraz 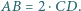 Punkt
Punkt 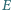 jest środkiem boku
jest środkiem boku 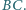 Udowodnić, że jeśli w czworokąt
Udowodnić, że jeśli w czworokąt 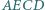 można wpisać okrąg, to
można wpisać okrąg, to 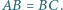
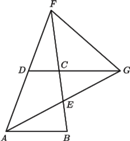
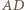 i
i 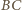 przecinają się w punkcie
przecinają się w punkcie 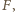 a proste
a proste 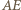 i
i 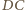 w punkcie
w punkcie 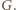
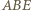 i
i 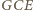 są przystające, a w szczególności
są przystające, a w szczególności 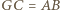 oraz
oraz 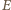 jest środkiem
jest środkiem 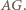 Ponadto
Ponadto 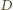 jest środkiem
jest środkiem 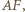 ponieważ odcinek
ponieważ odcinek 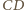 jest równoległy do
jest równoległy do 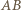 i dwa razy krótszy. Zatem
i dwa razy krótszy. Zatem 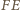 i
i 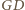 są środkowymi w trójkącie
są środkowymi w trójkącie 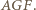
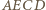 można wpisać okrąg, to zachodzi równość
można wpisać okrąg, to zachodzi równość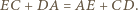
 i
i  które mają równe pola (równe połowie pola trójkąta
które mają równe pola (równe połowie pola trójkąta  ). W takim razie mają również równe obwody, czyli
). W takim razie mają również równe obwody, czyli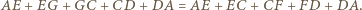
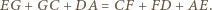
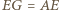 i
i 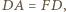 to mamy też
to mamy też 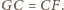 Stąd dostajemy
Stąd dostajemy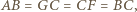
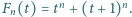 Udowodnić, że istnieje nieskończenie wiele liczb całkowitych
Udowodnić, że istnieje nieskończenie wiele liczb całkowitych 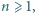 dla których równanie
dla których równanie 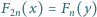 nie ma rozwiązań w liczbach całkowitych
nie ma rozwiązań w liczbach całkowitych 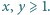
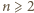 równanie może mieć w liczbach całkowitych
równanie może mieć w liczbach całkowitych 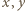 co najwyżej skończenie wiele rozwiązań (autor: Marcin Mazur); zaś w rocznym omówieniu (Delta 2/1992) pozostało otwarte pytanie, czy to równanie w ogóle ma rozwiązania poza trywialnymi
co najwyżej skończenie wiele rozwiązań (autor: Marcin Mazur); zaś w rocznym omówieniu (Delta 2/1992) pozostało otwarte pytanie, czy to równanie w ogóle ma rozwiązania poza trywialnymi 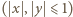 ; obecna propozycja to mały krok w kierunku próby badania tego problemu.
; obecna propozycja to mały krok w kierunku próby badania tego problemu. jest nieparzystą liczbą pierwszą, równanie
jest nieparzystą liczbą pierwszą, równanie 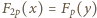 nie ma rozwiązań w liczbach całkowitych dodatnich.
nie ma rozwiązań w liczbach całkowitych dodatnich. jest rozwiązaniem. Zgodnie z małym twierdzeniem Fermata,
jest rozwiązaniem. Zgodnie z małym twierdzeniem Fermata,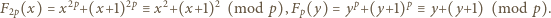
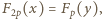 to
to 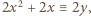 czyli
czyli 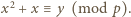
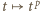 (w zbiorze liczb dodatnich) wynika nierówność
(w zbiorze liczb dodatnich) wynika nierówność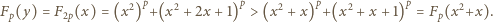
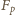 jest rosnąca; stąd
jest rosnąca; stąd 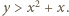 Skoro zaś
Skoro zaś 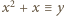 (mod
(mod 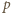 ), widzimy, że
), widzimy, że 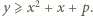 A zatem
A zatem 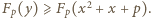 Aby uzyskać oczekiwaną sprzeczność, wystarczy wykazać, że
Aby uzyskać oczekiwaną sprzeczność, wystarczy wykazać, że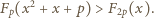
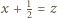 ; wtedy
; wtedy 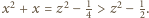 Ponownie korzystając z wypukłości funkcji
Ponownie korzystając z wypukłości funkcji 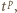 mamy nierówność
mamy nierówność 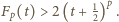 Wobec tego
Wobec tego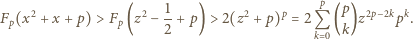
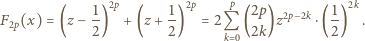
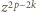 jest nie mniejszy niż analogiczny współczynnik w wyrażeniu (3); czyli, że
jest nie mniejszy niż analogiczny współczynnik w wyrażeniu (3); czyli, że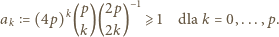
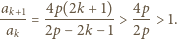
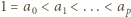 ; oszacowanie (4) gotowe, dowód zakończony.
; oszacowanie (4) gotowe, dowód zakończony.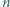 będzie ustaloną dodatnią liczbą nieparzystą. Wyznaczyć największą możliwą liczność zbioru złożonego z liczb całkowitych dodatnich, mniejszych od
będzie ustaloną dodatnią liczbą nieparzystą. Wyznaczyć największą możliwą liczność zbioru złożonego z liczb całkowitych dodatnich, mniejszych od 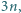 w którym każde dwa różne elementy mają i różnicę, i sumę różną od
w którym każde dwa różne elementy mają i różnicę, i sumę różną od 
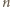 jest nieparzysta, zatem zbiór wszystkich liczb parzystych, mniejszych od
jest nieparzysta, zatem zbiór wszystkich liczb parzystych, mniejszych od 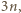 ma własność, o którą chodzi. Jest ich
ma własność, o którą chodzi. Jest ich 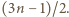 Wykażemy, że jest to największa możliwa liczność.
Wykażemy, że jest to największa możliwa liczność.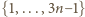 na rozłączne pary:
na rozłączne pary: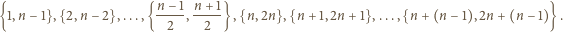
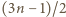 par liczb. Zbiór o większej liczności (zawarty w
par liczb. Zbiór o większej liczności (zawarty w 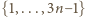 ) musi zawierać jedną z wymienionych par. Ale w każdej parze albo suma, albo różnica elementów jest równa
) musi zawierać jedną z wymienionych par. Ale w każdej parze albo suma, albo różnica elementów jest równa  Stąd nasza teza.
Stąd nasza teza.
 swoich ruchach Maja maluje na kolorowo
swoich ruchach Maja maluje na kolorowo  punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród
punktów z jednej prostej. Każdą parę takich kolorowych punktów można na dwa sposoby uzupełnić do trójkąta równobocznego, par punktów spośród  jest
jest 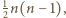 więc łącznie po
więc łącznie po 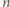 ruchach na płaszczyźnie jest
ruchach na płaszczyźnie jest 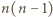 takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.
takich punktów, że pomalowanie dowolnego z nich na kolorowo da Mai zwycięstwo.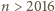 mamy
mamy 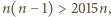 zatem Gucio nie może w swoich początkowych
zatem Gucio nie może w swoich początkowych 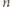 ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer
ruchach wszystkich opisanych powyżej punktów pomalować na czarno i Maja może wygrać w ruchu numer 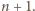
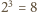 możliwych układów kolorów trójki wyróżnionych punktów z pojedynczej pionowej prostej. Ponieważ mamy 9 pionowych prostych, na pewnych dwóch z nich (nazwijmy je
możliwych układów kolorów trójki wyróżnionych punktów z pojedynczej pionowej prostej. Ponieważ mamy 9 pionowych prostych, na pewnych dwóch z nich (nazwijmy je  i
i  ) jest ten sam układ kolorów takiej trójki.
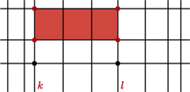
) jest ten sam układ kolorów takiej trójki. pomalowanych dwoma kolorami, pewne dwa punkty mają ten sam kolor. Niech to będą dwa wierzchołki szukanego prostokąta, pozostałe dwa to odpowiadające im punkty tego samego koloru z prostej
pomalowanych dwoma kolorami, pewne dwa punkty mają ten sam kolor. Niech to będą dwa wierzchołki szukanego prostokąta, pozostałe dwa to odpowiadające im punkty tego samego koloru z prostej 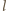 (leżą one na tych samych poziomych prostych).
(leżą one na tych samych poziomych prostych). kolorów
kolorów 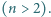 Wykaż, że istnieje na tej płaszczyźnie prostokąt o wierzchołkach jednego koloru.
Wykaż, że istnieje na tej płaszczyźnie prostokąt o wierzchołkach jednego koloru.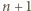 prostych poziomych oraz
prostych poziomych oraz 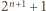 prostych pionowych.
prostych pionowych.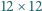 pomalowano jednym z trzech kolorów. Wykaż, że istnieją cztery pola o tym samym kolorze, których środki są wierzchołkami prostokąta.
pomalowano jednym z trzech kolorów. Wykaż, że istnieją cztery pola o tym samym kolorze, których środki są wierzchołkami prostokąta.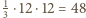 pól. Rozważmy 48 pól tego właśnie koloru i niech
pól. Rozważmy 48 pól tego właśnie koloru i niech 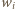 oznacza liczbę tych pól występujących w
oznacza liczbę tych pól występujących w 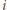 -tym wierszu; oczywiście
-tym wierszu; oczywiście 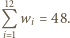 W każdym wierszu dwa spośród rozważanych pól można wybrać na
W każdym wierszu dwa spośród rozważanych pól można wybrać na 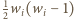 sposobów. Wobec tego
sposobów. Wobec tego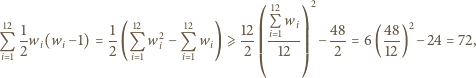
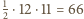 sposobów - mniej niż 72. Oznacza to, że w pewnych dwóch wierszach można wybrać po dwa pola tego samego koloru i w tych samych kolumnach; ich środki tworzą szukany prostokąt.
sposobów - mniej niż 72. Oznacza to, że w pewnych dwóch wierszach można wybrać po dwa pola tego samego koloru i w tych samych kolumnach; ich środki tworzą szukany prostokąt.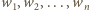 zachodzi nierówność między średnią kwadratową a arytmetyczną:
zachodzi nierówność między średnią kwadratową a arytmetyczną: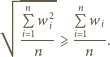
 rycerzy, w której nie będzie wrogów?
rycerzy, w której nie będzie wrogów?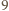 osób musimy wybrać
osób musimy wybrać 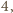 które nie siedzą na sąsiadujących miejscach. Możemy to zrobić na
które nie siedzą na sąsiadujących miejscach. Możemy to zrobić na 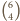 sposobów, ponieważ wybrane osoby jednoznacznie odpowiadają miejscom, a więc wstawieniu pomiędzy
sposobów, ponieważ wybrane osoby jednoznacznie odpowiadają miejscom, a więc wstawieniu pomiędzy 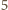 miejsc osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim)
miejsc osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim) 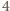 miejsc dla osób z drużyny.
miejsc dla osób z drużyny.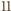 osób musimy wybrać
osób musimy wybrać 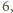 niebędących wrogami. W tym przypadku drużynę można wybrać na
niebędących wrogami. W tym przypadku drużynę można wybrać na 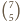 sposobów: pomiędzy
sposobów: pomiędzy 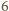 miejsc dla osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim) wstawiamy
miejsc dla osób spoza drużyny (lub przed pierwszym z nich, lub za ostatnim) wstawiamy 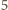 miejsc dla osób z drużyny.
miejsc dla osób z drużyny.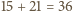 sposobów.
sposobów.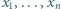 będą liczbami rzeczywistymi dodatnimi, przy czym
będą liczbami rzeczywistymi dodatnimi, przy czym 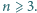 Dla wygody przyjmijmy dodatkowo, że
Dla wygody przyjmijmy dodatkowo, że 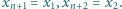 Udowodnić, że
Udowodnić, że
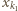 oznacza największą z liczb
oznacza największą z liczb 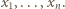 Popatrzmy na wyraz
Popatrzmy na wyraz 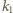 naszej sumy:
naszej sumy: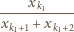
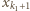 lub
lub 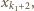 przez
przez 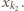 Popatrzmy teraz na wyraz
Popatrzmy teraz na wyraz 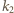 naszej sumy:
naszej sumy: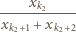
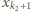 lub
lub 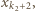 przez
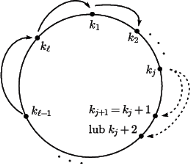
przez 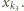 Kontynuując to postępowanie, otrzymujemy ciąg indeksów
Kontynuując to postępowanie, otrzymujemy ciąg indeksów 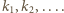
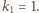 Z definicji mamy
Z definicji mamy 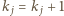 lub
lub 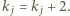 Zatem po pewnej liczbie kroków po raz pierwszy otrzymamy
Zatem po pewnej liczbie kroków po raz pierwszy otrzymamy 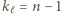 lub
lub 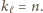 Ponadto
Ponadto 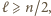 bo w każdym kroku przesuwamy się o co najwyżej dwa. Zauważmy też, że
bo w każdym kroku przesuwamy się o co najwyżej dwa. Zauważmy też, że 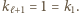
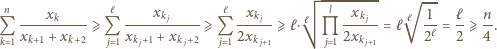

 boki
boki 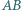 i
i 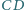 są równoległe oraz
są równoległe oraz 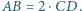 Punkt
Punkt 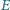 jest środkiem boku
jest środkiem boku 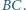 Udowodnić, że jeśli
Udowodnić, że jeśli 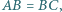 to w czworokąt
to w czworokąt 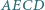 można wpisać okrąg.
można wpisać okrąg.
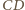 punkt
punkt 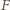 w taki sposób, aby czworokąt
w taki sposób, aby czworokąt 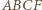 był równoległobokiem.
był równoległobokiem.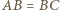 możemy wywnioskować, że
możemy wywnioskować, że 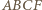 jest rombem. Ponadto, skoro
jest rombem. Ponadto, skoro 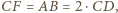 to punkt
to punkt 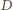 jest środkiem boku
jest środkiem boku 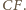 Ponieważ punkt
Ponieważ punkt 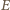 jest środkiem boku
jest środkiem boku 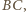 więc punkty
więc punkty 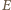 i
i 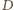 są symetryczne względem prostej
są symetryczne względem prostej 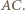 Oznacza to, że czworokąt
Oznacza to, że czworokąt 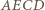 jest deltoidem, zatem w szczególności można w niego wpisać okrąg.
jest deltoidem, zatem w szczególności można w niego wpisać okrąg.