Niech 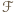 będzie rodziną
będzie rodziną  podzbiorów zbioru
podzbiorów zbioru 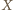 , spełniającą zadane warunki. Jeżeli do
, spełniającą zadane warunki. Jeżeli do 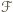 należy zbiór pusty lub zbiór pełny (cały zbiór
należy zbiór pusty lub zbiór pełny (cały zbiór 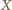 ), to już żaden inny zbiór nie może do
), to już żaden inny zbiór nie może do 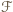 należeć. W tym przypadku
należeć. W tym przypadku 
Jeżeli do 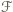 należy pewien zbiór jednoelementowy
należy pewien zbiór jednoelementowy 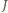 oraz pewien zbiór
oraz pewien zbiór 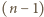 -elementowy
-elementowy 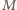 , to muszą się one dopełniać (bo inaczej
, to muszą się one dopełniać (bo inaczej 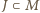 ) oraz żaden inny zbiór nie może do
) oraz żaden inny zbiór nie może do 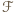 należeć (bo albo zawiera
należeć (bo albo zawiera 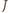 , albo jest zawarty w
, albo jest zawarty w 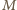 ). W tym przypadku
). W tym przypadku 
Przyjmijmy dalej, że żadna z tych sytuacji nie ma miejsca. Wszystkie zbiory w 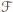 mają z założenia różne liczności. Wykluczone zostały liczności
mają z założenia różne liczności. Wykluczone zostały liczności 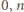 oraz albo
oraz albo 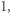 albo
albo 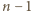 . Pozostaje
. Pozostaje 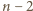 możliwych liczności. Zatem
możliwych liczności. Zatem 
Pokażemy teraz, że dla każdego 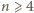 istnieje w zbiorze
istnieje w zbiorze 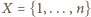 rodzina
rodzina 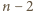 podzbiorów
podzbiorów 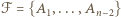 o wymaganych własnościach. Najpierw przykłady dla
o wymaganych własnościach. Najpierw przykłady dla 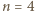 ,
, 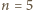 :
:
Dalej indukcja ze skokiem o 2. Niech 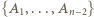 będzie "dobrą" rodziną podzbiorów zbioru
będzie "dobrą" rodziną podzbiorów zbioru 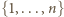 , ponumerowanych tak, że
, ponumerowanych tak, że 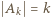 dla
dla 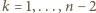 . Bierzemy zbiór
. Bierzemy zbiór 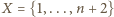 i określamy:
i określamy:
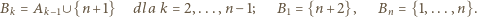
Widać, że 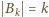 dla
dla 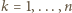 i że żaden ze zbiorów
i że żaden ze zbiorów 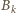 nie jest podzbiorem innego. Tak więc
nie jest podzbiorem innego. Tak więc 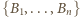 jest rodziną podzbiorów
jest rodziną podzbiorów 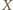 , o jaką chodzi.
, o jaką chodzi.
Dostajemy odpowiedź: dla każdej liczby 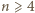 maksymalna liczność rodziny
maksymalna liczność rodziny 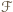 wynosi
wynosi 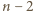 .
.
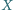 będzie zbiorem
będzie zbiorem  -elementowym (
-elementowym ( 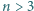 ). Wyznaczyć największą liczbę
). Wyznaczyć największą liczbę 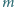 , dla której w zbiorze
, dla której w zbiorze 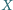 istnieje
istnieje  podzbiorów, z których żaden nie zawiera się w innym oraz żaden nie jest równoliczny z innym.
podzbiorów, z których żaden nie zawiera się w innym oraz żaden nie jest równoliczny z innym.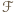 będzie rodziną
będzie rodziną  podzbiorów zbioru
podzbiorów zbioru 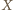 , spełniającą zadane warunki. Jeżeli do
, spełniającą zadane warunki. Jeżeli do 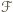 należy zbiór pusty lub zbiór pełny (cały zbiór
należy zbiór pusty lub zbiór pełny (cały zbiór 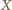 ), to już żaden inny zbiór nie może do
), to już żaden inny zbiór nie może do 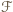 należeć. W tym przypadku
należeć. W tym przypadku 
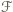 należy pewien zbiór jednoelementowy
należy pewien zbiór jednoelementowy 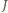 oraz pewien zbiór
oraz pewien zbiór 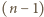 -elementowy
-elementowy 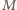 , to muszą się one dopełniać (bo inaczej
, to muszą się one dopełniać (bo inaczej 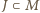 ) oraz żaden inny zbiór nie może do
) oraz żaden inny zbiór nie może do 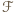 należeć (bo albo zawiera
należeć (bo albo zawiera 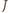 , albo jest zawarty w
, albo jest zawarty w 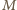 ). W tym przypadku
). W tym przypadku 
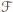 mają z założenia różne liczności. Wykluczone zostały liczności
mają z założenia różne liczności. Wykluczone zostały liczności 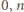 oraz albo
oraz albo 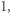 albo
albo 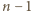 . Pozostaje
. Pozostaje 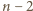 możliwych liczności. Zatem
możliwych liczności. Zatem 
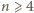 istnieje w zbiorze
istnieje w zbiorze 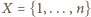 rodzina
rodzina 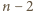 podzbiorów
podzbiorów 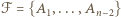 o wymaganych własnościach. Najpierw przykłady dla
o wymaganych własnościach. Najpierw przykłady dla 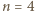 ,
, 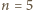 :
: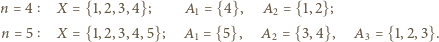
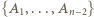 będzie "dobrą" rodziną podzbiorów zbioru
będzie "dobrą" rodziną podzbiorów zbioru 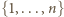 , ponumerowanych tak, że
, ponumerowanych tak, że 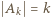 dla
dla 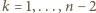 . Bierzemy zbiór
. Bierzemy zbiór 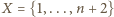 i określamy:
i określamy: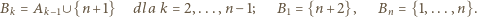
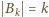 dla
dla 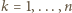 i że żaden ze zbiorów
i że żaden ze zbiorów 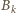 nie jest podzbiorem innego. Tak więc
nie jest podzbiorem innego. Tak więc 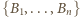 jest rodziną podzbiorów
jest rodziną podzbiorów 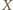 , o jaką chodzi.
, o jaką chodzi.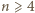 maksymalna liczność rodziny
maksymalna liczność rodziny 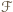 wynosi
wynosi 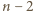 .
.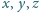 :
:
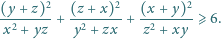
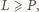 gdzie
gdzie
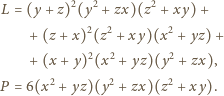
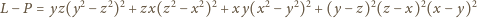
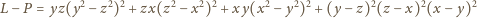
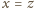 różnica
różnica
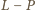 przyjmuje wartość
przyjmuje wartość
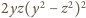 ; analogicznie dla
; analogicznie dla
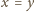 i dla
i dla
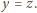 Zatem
przyjmując
Zatem
przyjmując
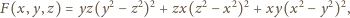
 ma wartość zero, gdy dowolne
dwie zmienne są równe. Jest więc podzielny przez wielomian
ma wartość zero, gdy dowolne
dwie zmienne są równe. Jest więc podzielny przez wielomian
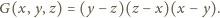
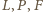 są wielomianami symetrycznymi, natomiast
są wielomianami symetrycznymi, natomiast
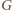 jest
wielomianem antysymetrycznym (zmienia znak przy transpozycji zmiennych),
wynika stąd, że iloraz
jest
wielomianem antysymetrycznym (zmienia znak przy transpozycji zmiennych),
wynika stąd, że iloraz
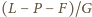 też jest antysymetryczny – ma
więc wartość zero, gdy dwie zmienne są równe, i w konsekwencji dzieli się
znów przez
też jest antysymetryczny – ma
więc wartość zero, gdy dwie zmienne są równe, i w konsekwencji dzieli się
znów przez
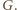 To znaczy, że wielomian
To znaczy, że wielomian
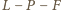 dzieli się przez
dzieli się przez
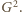 Są to wielomiany jednorodne szóstego stopnia, ich iloraz musi być
stałą.
Są to wielomiany jednorodne szóstego stopnia, ich iloraz musi być
stałą.
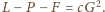 Wartość stałej
Wartość stałej
 znajdujemy,
podstawiając w miejsce
znajdujemy,
podstawiając w miejsce
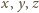 dowolne trzy różne liczby; wychodzi
dowolne trzy różne liczby; wychodzi
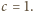 Tak więc
Tak więc
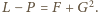 Jest to właśnie „ta zmyślna”
tożsamość.
Jest to właśnie „ta zmyślna”
tożsamość.
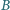 zbioru
zbioru
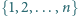 , który nie zawiera
żadnej pary liczb kolejnych, przyporządkowujemy liczbę
, który nie zawiera
żadnej pary liczb kolejnych, przyporządkowujemy liczbę
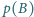 , będącą
iloczynem liczb w zbiorze
, będącą
iloczynem liczb w zbiorze
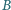 (dla zbioru pustego przyjmujemy
(dla zbioru pustego przyjmujemy
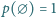 ). Obliczyć sumę kwadratów wszystkich uzyskanych
liczb
). Obliczyć sumę kwadratów wszystkich uzyskanych
liczb
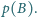
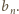 Weźmy pod uwagę wszystkie te
podzbiory
Weźmy pod uwagę wszystkie te
podzbiory
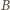 zbioru
zbioru
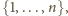 które nie zawierają żadnej pary
liczb kolejnych i do których nie należy liczba
które nie zawierają żadnej pary
liczb kolejnych i do których nie należy liczba
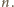 Są to więc podzbiory
zbioru
Są to więc podzbiory
zbioru
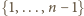 ; suma kwadratów uzyskanych dla nich liczb
; suma kwadratów uzyskanych dla nich liczb
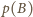 wynosi
wynosi
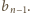 Z kolei zbiory
Z kolei zbiory
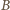 (bez pary liczb
kolejnych), do których liczba
(bez pary liczb
kolejnych), do których liczba
 należy, traktujemy jak podzbiory zbioru
należy, traktujemy jak podzbiory zbioru
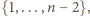 z dołączonym elementem
z dołączonym elementem
 ; suma kwadratów
uzyskanych dla nich liczb
; suma kwadratów
uzyskanych dla nich liczb
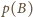 wynosi
wynosi
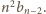 Dostajemy wzór
rekurencyjny
Dostajemy wzór
rekurencyjny
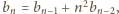 który z wartościami początkowymi
który z wartościami początkowymi
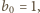
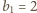 prowadzi przez łatwą indukcję do wyniku w jawnej
postaci:
prowadzi przez łatwą indukcję do wyniku w jawnej
postaci:
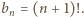
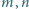 i dla
dowolnych liczb rzeczywistych nieujemnych
i dla
dowolnych liczb rzeczywistych nieujemnych
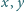 spełniających warunek
spełniających warunek
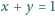 zachodzi nierówność
zachodzi nierówność
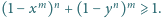
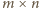 i na każdym polu dokonajmy
losowania: z prawdopodobieństwem
i na każdym polu dokonajmy
losowania: z prawdopodobieństwem
 postawimy tam biały
pionek, a z prawdopodobieństwem
postawimy tam biały
pionek, a z prawdopodobieństwem
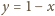 – czarny. Wówczas
prawdopodobieństwo tego, że na każdym z
– czarny. Wówczas
prawdopodobieństwo tego, że na każdym z
 pól wybranej kolumny
stoi biały pionek, jest równe
pól wybranej kolumny
stoi biały pionek, jest równe
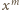 . W takim razie
. W takim razie
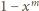 to
prawdopodobieństwo tego, że w tej kolumnie znajdzie się chociaż jeden
pionek czarny, a
to
prawdopodobieństwo tego, że w tej kolumnie znajdzie się chociaż jeden
pionek czarny, a
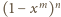 możemy zinterpretować jako szansę na
to, że w każdej kolumnie będzie przynajmniej jeden czarny pionek.
Podobnie
możemy zinterpretować jako szansę na
to, że w każdej kolumnie będzie przynajmniej jeden czarny pionek.
Podobnie
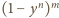 to szansa zdarzenia, że w każdym wierszu jest
co najmniej jeden biały pionek. Zauważmy jednak, że któreś z tych
zdarzeń musi wystąpić, ponieważ jeżeli jakaś kolumna zawiera same
białe pionki, to w każdym wierszu jest już biały pionek. To dowodzi
podanej nierówności.
to szansa zdarzenia, że w każdym wierszu jest
co najmniej jeden biały pionek. Zauważmy jednak, że któreś z tych
zdarzeń musi wystąpić, ponieważ jeżeli jakaś kolumna zawiera same
białe pionki, to w każdym wierszu jest już biały pionek. To dowodzi
podanej nierówności.
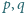 , że
, że
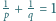 .
Udowodnić, że każda liczba całkowita dodatnia występuje dokładnie raz
w dokładnie jednym z ciągów
.
Udowodnić, że każda liczba całkowita dodatnia występuje dokładnie raz
w dokładnie jednym z ciągów
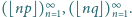
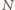 będzie liczbą całkowitą dodatnią. Zastanówmy się, ile jest liczb
mniejszych od
będzie liczbą całkowitą dodatnią. Zastanówmy się, ile jest liczb
mniejszych od
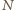 , które występują w obu danych ciągach (każdą liczbę
liczymy tyle razy, ile razy wystąpiła). Otóż nierówność
, które występują w obu danych ciągach (każdą liczbę
liczymy tyle razy, ile razy wystąpiła). Otóż nierówność
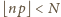 jest
równoważna
jest
równoważna
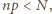 innymi słowy
innymi słowy
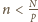 . To oznacza, że
w pierwszym ciągu takich liczb mamy dokładnie
. To oznacza, że
w pierwszym ciągu takich liczb mamy dokładnie
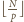 . Analogicznie
w drugim ciągu jest ich
. Analogicznie
w drugim ciągu jest ich
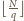 , co łącznie daje
, co łącznie daje
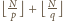 . Dla liczby
niewymiernej
. Dla liczby
niewymiernej
 mamy
mamy
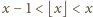 , stąd:
, stąd:
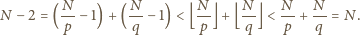
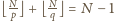 , bo jest to liczba całkowita. Wiemy
w takim razie, że liczb mniejszych od
, bo jest to liczba całkowita. Wiemy
w takim razie, że liczb mniejszych od
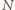 jest w obu tych ciągach
dokładnie
jest w obu tych ciągach
dokładnie
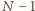 . Podobnie dowodzimy, że liczb mniejszych od
. Podobnie dowodzimy, że liczb mniejszych od
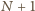 jest dokładnie
jest dokładnie
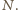 Odejmując te wyniki, wnioskujemy, że
liczba
Odejmując te wyniki, wnioskujemy, że
liczba
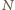 pojawia się w tych ciągach dokładnie raz.
pojawia się w tych ciągach dokładnie raz.
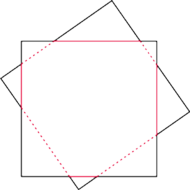
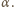 Oznaczając sumę długości
kolorowych odcinków ciągłych przez
Oznaczając sumę długości
kolorowych odcinków ciągłych przez
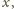 a przerywanych przez
a przerywanych przez
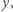 widać, że obwód jednego kwadratu jest równy
widać, że obwód jednego kwadratu jest równy
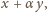 a drugiego
a drugiego
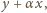 co po przyrównaniu daje
co po przyrównaniu daje
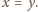
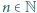 prawdziwe są poniższe nierówności
pomiędzy średnią arytmetyczną i geometryczną
prawdziwe są poniższe nierówności
pomiędzy średnią arytmetyczną i geometryczną
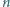 dodatnich liczb
rzeczywistych.
dodatnich liczb
rzeczywistych.

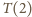 jest standardową szkolną nierównością.
Ponadto jeżeli zachodzi
jest standardową szkolną nierównością.
Ponadto jeżeli zachodzi
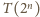 dla pewnego naturalnego
dla pewnego naturalnego
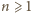 , to
dla
, to
dla
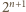 liczb dodatnich mamy
liczb dodatnich mamy
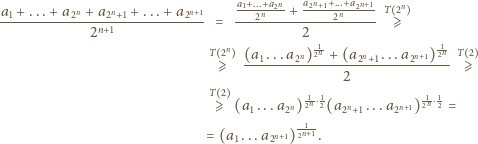
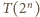 zachodzi dla dowolnej liczby
naturalnej
zachodzi dla dowolnej liczby
naturalnej
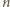 . Pozostała do wykazania prawdziwość implikacji
. Pozostała do wykazania prawdziwość implikacji
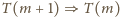 .
.
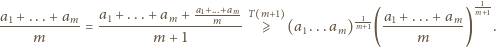
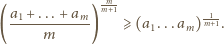
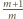 , kończymy
dowód.
, kończymy
dowód.
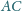 i
i
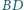 czworokąta wypukłego
czworokąta wypukłego
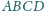 przecinają
się w punkcie
przecinają
się w punkcie
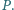 Punkt
Punkt
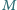 jest środkiem boku
jest środkiem boku
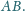 Prosta
Prosta
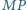 przecina bok
przecina bok
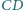 w punkcie
w punkcie
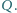 Udowodnij, że
stosunek pól trójkątów
Udowodnij, że
stosunek pól trójkątów
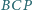 i
i
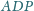 jest równy stosunkowi
długości odcinków
jest równy stosunkowi
długości odcinków
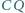 i
i
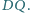
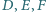 należą odpowiednio do boków
należą odpowiednio do boków
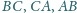 trójkąta ostrokątnego
trójkąta ostrokątnego
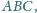 przy czym
przy czym
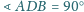 oraz
oraz
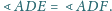 Wykaż, że proste
Wykaż, że proste
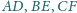 przecinają się
w jednym punkcie.
przecinają się
w jednym punkcie.
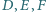 są punktami styczności okręgów dopisanych do trójkąta
są punktami styczności okręgów dopisanych do trójkąta
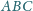 odpowiednio do boków
odpowiednio do boków
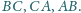 Wykaż, że
proste
Wykaż, że
proste
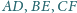 przecinają się w jednym punkcie (tzw. punkcie
Nagela).
przecinają się w jednym punkcie (tzw. punkcie
Nagela).
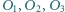 o środkach
odpowiednio
o środkach
odpowiednio
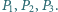 Te dwie styczne do obu okręgów
Te dwie styczne do obu okręgów
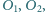 które rozdzielają te okręgi, przecinają się w punkcie
które rozdzielają te okręgi, przecinają się w punkcie
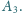 Punkty
Punkty
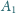 i
i
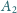 zdefiniowane są analogicznie. Wykaż, że proste
zdefiniowane są analogicznie. Wykaż, że proste
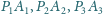 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
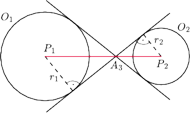
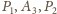 są współliniowe i z twierdzenia Talesa
są współliniowe i z twierdzenia Talesa
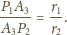
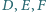 należą odpowiednio do boków
należą odpowiednio do boków
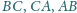 trójkąta
trójkąta
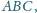 proste
proste
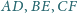 przecinają się w jednym
punkcie. Proste
przecinają się w jednym
punkcie. Proste
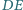 i
i
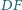 przecinają prostą równoległą do
przecinają prostą równoległą do
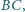 przechodzącą przez punkt
przechodzącą przez punkt
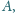 odpowiednio w punktach
odpowiednio w punktach
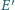 i
i
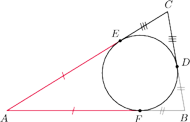
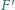 . Udowodnij, że punkt
. Udowodnij, że punkt
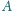 jest środkiem odcinka
jest środkiem odcinka
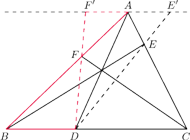
 , to
, to
 Stąd
Stąd

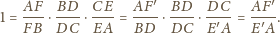
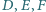 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt
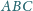 odpowiednio do boków
odpowiednio do boków
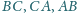 . Wykaż, że
proste
. Wykaż, że
proste
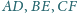 przecinają się w jednym punkcie (tzw. punkcie
Gergonne’a).
przecinają się w jednym punkcie (tzw. punkcie
Gergonne’a).
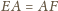 ,
,
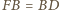 ,
,
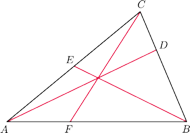
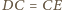 . Stąd
. Stąd
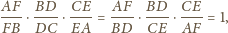
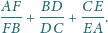
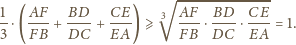
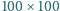 wpisano liczbę rzeczywistą.
Okazało się, że suma liczb wpisanych w każde cztery pola, które można
nakryć
wpisano liczbę rzeczywistą.
Okazało się, że suma liczb wpisanych w każde cztery pola, które można
nakryć 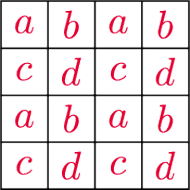
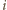 -ty wiersz i
-ty wiersz i
 -tą kolumnę tablicy
przez
-tą kolumnę tablicy
przez
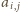 , gdzie
, gdzie
 . Przykrywając L-tetraminem liczby
. Przykrywając L-tetraminem liczby
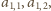
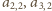 , a następnie liczby
, a następnie liczby
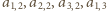 ,
stwierdzamy, że
,
stwierdzamy, że
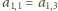 . Postępując analogicznie, zauważamy,
że
. Postępując analogicznie, zauważamy,
że
 dla
dla
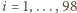 ,
,
 oraz
oraz
 dla
dla
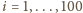 ,
,
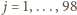 . Otrzymany
wynik oznacza, że rozważana tablica jest okresowa o okresie
. Otrzymany
wynik oznacza, że rozważana tablica jest okresowa o okresie
 . Innymi
słowy, dowolny kwadrat wymiaru
. Innymi
słowy, dowolny kwadrat wymiaru
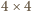 , zawarty w tej tablicy, ma postać
jak na rysunku 2. Przykrywając L-tetraminem pierwsze dwie kolumny
rozważanego kwadratu, wnioskujemy, że
, zawarty w tej tablicy, ma postać
jak na rysunku 2. Przykrywając L-tetraminem pierwsze dwie kolumny
rozważanego kwadratu, wnioskujemy, że
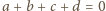 . Przykrywając
L-tetraminem liczby
. Przykrywając
L-tetraminem liczby
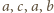 , otrzymujemy
, otrzymujemy
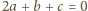 , co razem
z poprzednią równością daje
, co razem
z poprzednią równością daje
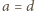 . Przykrywając L-tetraminem liczby
. Przykrywając L-tetraminem liczby
 , wnioskujemy analogicznie, że
, wnioskujemy analogicznie, że
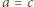 . Zatem rozważana
tablica zawiera tylko dwie różne liczby
. Zatem rozważana
tablica zawiera tylko dwie różne liczby
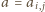 dla
dla
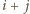 parzystych
i
parzystych
i
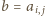 dla
dla
 nieparzystych. Ponadto widzimy, że
nieparzystych. Ponadto widzimy, że
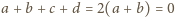 . Stąd suma wszystkich liczb stojących na obu
głównych przekątnych tablicy wynosi
. Stąd suma wszystkich liczb stojących na obu
głównych przekątnych tablicy wynosi
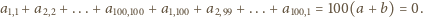
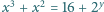 w liczbach całkowitych
w liczbach całkowitych
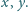
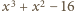 może dać
przy dzieleniu przez 7 wszystkie reszty z wyjątkiem 2 oraz 4. Potęgi dwójki
dają jedynie reszty 1, 2, 4. Rozważane równanie może więc być spełnione
tylko wtedy, gdy
może dać
przy dzieleniu przez 7 wszystkie reszty z wyjątkiem 2 oraz 4. Potęgi dwójki
dają jedynie reszty 1, 2, 4. Rozważane równanie może więc być spełnione
tylko wtedy, gdy
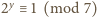 ; to zaś ma miejsce jedynie dla
wykładników
; to zaś ma miejsce jedynie dla
wykładników
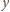 podzielnych przez 3.
podzielnych przez 3.
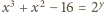 jest spełnione, to
jest spełnione, to
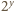 jest sześcianem liczby całkowitej. Dla liczb całkowitych
jest sześcianem liczby całkowitej. Dla liczb całkowitych
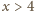 wartość
wartość
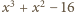 leży pomiędzy
leży pomiędzy
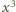 a
a
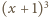 , więc
nie jest sześcianem. Dla
, więc
nie jest sześcianem. Dla
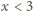 wartość
wartość
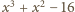 jest
ujemna. Dla
jest
ujemna. Dla
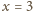 dostajemy równanie sprzeczne
dostajemy równanie sprzeczne
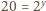 .
Pozostaje wartość
.
Pozostaje wartość
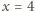 , która wraz z
, która wraz z
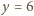 daje jedyne
rozwiązanie równania.
daje jedyne
rozwiązanie równania.
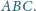 Rozważamy punkt
Rozważamy punkt
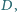 zmieniający swoje
położenie na boku
zmieniający swoje
położenie na boku
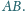 Prosta styczna do okręgów wpisanych
w trójkąty
Prosta styczna do okręgów wpisanych
w trójkąty
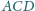 i
i
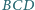 , rozłączna z odcinkiem
, rozłączna z odcinkiem
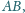 przecina odcinek
przecina odcinek
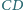 w punkcie
w punkcie
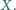 Udowodnić, że wszystkie
uzyskane w ten sposób punkty
Udowodnić, że wszystkie
uzyskane w ten sposób punkty
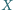 leżą na pewnym okręgu.
leżą na pewnym okręgu.
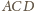 i
i
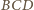 są
styczne do boku
są
styczne do boku
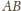 odpowiednio w punktach
odpowiednio w punktach
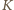 i
i
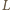 ;
do prostej przechodzącej przez
;
do prostej przechodzącej przez
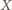 – odpowiednio w punktach
– odpowiednio w punktach
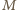 i
i
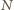 ; zaś do odcinka
; zaś do odcinka
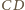 – odpowiednio w punktach
– odpowiednio w punktach
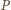 i
i
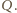
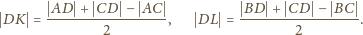
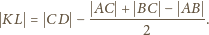
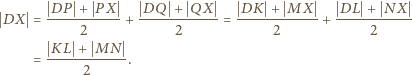
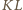 i
i
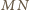 są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
są symetryczne względem wspólnej osi
symetrii obu okręgów. Możemy zatem przepisać ostatnią równość jako
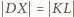 .
.
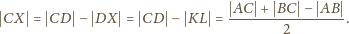
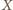 leży na okręgu o środku
leży na okręgu o środku
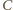 i promieniu
zależnym jedynie od trójkąta
i promieniu
zależnym jedynie od trójkąta
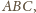 a nie od położenia punktu
a nie od położenia punktu
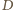 na boku
na boku
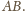
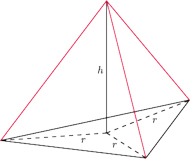
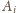 oraz
długość krawędzi wychodzących z wierzchołka
oraz
długość krawędzi wychodzących z wierzchołka
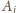 przez
przez
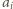 ,
gdzie
,
gdzie
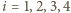 . Wtedy krawędź
. Wtedy krawędź
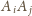 , gdzie
, gdzie
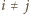 ,
wychodzi z wierzchołka
,
wychodzi z wierzchołka
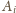 oraz z wierzchołka
oraz z wierzchołka
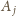 . Oznacza to,
że
. Oznacza to,
że
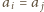 , a więc czworościan jest foremny.
, a więc czworościan jest foremny.
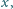 niecałkowite, dla których
wartość wyrażenia
niecałkowite, dla których
wartość wyrażenia
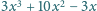 jest liczbą całkowitą.
jest liczbą całkowitą.
 będzie jedną z szukanych liczb. Zapisujemy ją
w postaci nieskracalnego ułamka
będzie jedną z szukanych liczb. Zapisujemy ją
w postaci nieskracalnego ułamka
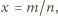 o mianowniku
o mianowniku
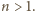 Liczba
Liczba
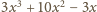 ma być całkowita, co oznacza, że
ma być całkowita, co oznacza, że
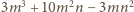 dzieli się przez
dzieli się przez
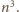 Stąd w szczególności
wynika, że
Stąd w szczególności
wynika, że
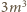 dzieli się przez
dzieli się przez
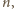 więc
więc
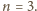 Zatem
Zatem
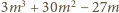 dzieli się przez 27.
dzieli się przez 27.
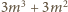 jest podzielna przez 27; innymi
słowy,
jest podzielna przez 27; innymi
słowy,
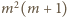 dzieli się przez 9. Skoro zaś
dzieli się przez 9. Skoro zaś
 jest liczbą
względnie pierwszą z
jest liczbą
względnie pierwszą z
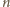 (czyli z 3), liczba
(czyli z 3), liczba
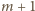 musi być
podzielna przez 9.
musi być
podzielna przez 9.
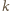 całkowitego mamy więc
całkowitego mamy więc
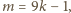 skąd
skąd
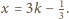 Na odwrót, gdy
Na odwrót, gdy
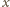 ma taką postać, wówczas liczba
ma taką postać, wówczas liczba
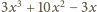 jest całkowita – o czym można się przekonać, analizując
„wstecz” wcześniejsze rozumowanie, albo po prostu sprawdzając rachunkiem,
że wartość tego wyrażenia wynosi
jest całkowita – o czym można się przekonać, analizując
„wstecz” wcześniejsze rozumowanie, albo po prostu sprawdzając rachunkiem,
że wartość tego wyrażenia wynosi
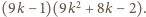
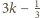 (
(
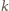 całkowite).
całkowite).
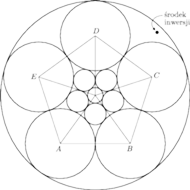
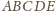 i rysujemy pięć
okręgów o środkach w jego wierzchołkach, o jednakowym promieniu
i rysujemy pięć
okręgów o środkach w jego wierzchołkach, o jednakowym promieniu
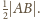 Niech
Niech
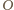 będzie środkiem pięciokąta. W trójkącie
będzie środkiem pięciokąta. W trójkącie
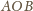 umieszczamy okrąg styczny do odcinków
umieszczamy okrąg styczny do odcinków
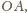
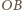 oraz do
narysowanych już okręgów o środkach
oraz do
narysowanych już okręgów o środkach
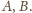 Podobne okręgi umieszczamy
w trójkątach
Podobne okręgi umieszczamy
w trójkątach
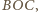
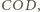
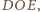
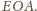 Wreszcie
rysujemy dwa okręgi o środku
Wreszcie
rysujemy dwa okręgi o środku
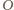 : mały, styczny zewnętrznie do pięciu
okręgów, narysowanych przed chwilą – oraz duży, styczny do pięciu okręgów,
narysowanych na początku i zawierający je wewnątrz.
: mały, styczny zewnętrznie do pięciu
okręgów, narysowanych przed chwilą – oraz duży, styczny do pięciu okręgów,
narysowanych na początku i zawierający je wewnątrz.