Zadanie ZM-1499
o zadaniu...
- Publikacja w Delcie: lipiec 2016
- Publikacja elektroniczna: 1 lipca 2016
Czy istnieje wielokrotność liczby 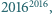 której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
Czy istnieje wielokrotność liczby 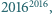 której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
której zapis w systemie dziesiętnym zawiera wszystkie dziesięć cyfr?
Czy istnieją takie funkcje kwadratowe 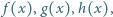 że równanie
że równanie 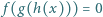 jest spełnione przez liczby 0, 1, 2, 3, 4, 5, 6, 7?
jest spełnione przez liczby 0, 1, 2, 3, 4, 5, 6, 7?
Trójkąt 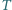 rozcięto wzdłuż odcinka na dwa trójkąty
rozcięto wzdłuż odcinka na dwa trójkąty 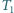 i
i 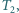 a trójkąt
a trójkąt 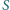 - na trójkąty
- na trójkąty 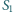 i
i 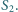 Okazało się, że trójkąt
Okazało się, że trójkąt 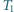 jest przystający do trójkąta
jest przystający do trójkąta 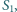 a trójkąt
a trójkąt 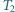 jest przystający do trójkąta
jest przystający do trójkąta 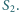 Czy wynika z tego, że trójkąty
Czy wynika z tego, że trójkąty 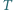 i
i 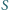 są przystające?
są przystające?
Dane są trójkąty 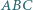 i
i 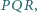 przy czym
przy czym 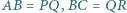 oraz
oraz 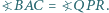 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?
Trójkąty 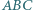 i
i 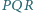 mają równe pola oraz
mają równe pola oraz 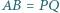 i
i 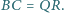 Czy wynika z tego, że trójkąty te są przystające?
Czy wynika z tego, że trójkąty te są przystające?
Czworokąty wypukłe 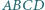 i
i 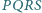 mają równe pola oraz
mają równe pola oraz 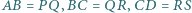 i
i 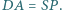 Czy wynika z tego, że czworokąty te są przystające?
Czy wynika z tego, że czworokąty te są przystające?
Przekątna pewnego czworokąta wypukłego dzieli go na dwa trójkąty równoramienne. Czy wynika z tego, że czworokąt ten jest deltoidem lub równoległobokiem?
Pewien sześciokąt wypukły ma wszystkie kąty równe 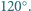 Czy wynika z tego, że jest on foremny?
Czy wynika z tego, że jest on foremny?
Punkt 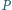 leży wewnątrz trójkąta ostrokątnego
leży wewnątrz trójkąta ostrokątnego 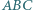 oraz
oraz 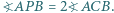 Czy wynika z tego, że
Czy wynika z tego, że 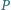 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 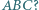
Pewna ściana wielościanu ma  boków. Czy wynika z tego, że ściana ta graniczy z
boków. Czy wynika z tego, że ściana ta graniczy z  innymi ścianami tego wielościanu?
innymi ścianami tego wielościanu?
Dwie spośród ścian pewnego wielościanu są przystającymi wielokątami położonymi w równoległych płaszczyznach, przy czym jedną z nich można tak przesunąć, by uzyskać drugą. Wszystkie pozostałe ściany tego wielościanu są równoległobokami. Czy wynika z tego, że rozważany wielościan jest graniastosłupem?
W trójkącie równoramiennym 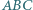 kąt przy wierzchołku
kąt przy wierzchołku 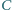 ma miarę
ma miarę 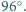 Wewnątrz trójkąta leży taki punkt
Wewnątrz trójkąta leży taki punkt 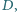 że
że 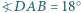 i
i 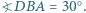 Wyznaczyć miarę kąta
Wyznaczyć miarę kąta 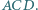
Każda z liczb całkowitych 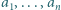 jest mniejsza od
jest mniejsza od 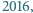 a najmniejsza wspólna wielokrotność dowolnych dwóch z tych liczb jest większa od
a najmniejsza wspólna wielokrotność dowolnych dwóch z tych liczb jest większa od 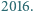 Wykazać, że
Wykazać, że

Mając dane parami różne liczby 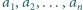 i
i 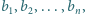 tworzymy tabelę
tworzymy tabelę 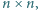 wpisując w
wpisując w 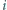 -tym wierszu i
-tym wierszu i 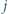 -tej kolumnie liczbę
-tej kolumnie liczbę 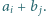 Wykazać, że jeśli iloczyn liczb wpisanych w każdą kolumnę jest jednakowy, to również iloczyn liczb wpisanych w każdy wiersz jest jednakowy.
Wykazać, że jeśli iloczyn liczb wpisanych w każdą kolumnę jest jednakowy, to również iloczyn liczb wpisanych w każdy wiersz jest jednakowy.
Zadanie 724 zostało opracowane na podstawie propozycji, którą przysłał pan Paweł Najman z Krakowa.
Dowieść, że liczby zespolone 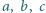 spełniają równanie
spełniają równanie
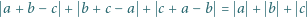
wtedy i tylko wtedy, gdy spełniają równanie
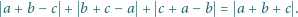
Czy każdy ściśle rosnący ciąg arytmetyczny o wyrazach całkowitych ma wyraz, będący jednocześnie pewnym wyrazem ciągu Fibonacciego 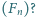

Zadanie 722 zaproponował pan Witold Bednarek z Łodzi.
Rozwiązać równanie 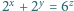 w liczbach całkowitych dodatnich
w liczbach całkowitych dodatnich 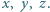
Na bokach 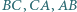 trójkąta
trójkąta 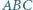 leżą punkty
leżą punkty 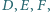 w których okręgi dopisane do trójkąta są styczne do tych boków. Niech
w których okręgi dopisane do trójkąta są styczne do tych boków. Niech 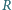 i
i  będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów
będą promieniami okręgów opisanego i wpisanego. Dowieść, że stosunek pól trójkątów 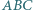 i
i 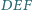 wynosi
wynosi 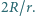
Przekątne czworokąta 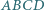 wpisanego w okrąg o środku
wpisanego w okrąg o środku 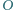 przecinają się w punkcie
przecinają się w punkcie 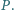 Niech
Niech 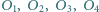 będą środkami okręgów opisanych odpowiednio na trójkątach
będą środkami okręgów opisanych odpowiednio na trójkątach 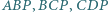 i
i 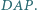 Wykazać, że proste
Wykazać, że proste 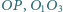 i
i 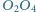 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Wyznaczyć największą liczbę naturalną 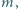 dla której istnieją takie liczby naturalne
dla której istnieją takie liczby naturalne 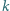 i
i 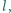 że spełnione jest równanie
że spełnione jest równanie
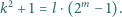
W wierzchołkach dwunastościanu foremnego umieszczamy parami różne liczby naturalne, a następnie każdej krawędzi przypisujemy największy wspólny dzielnik liczb z jej końców. Czy możemy zrobić to w taki sposób, by suma liczb w wierzchołkach była równa sumie liczb na krawędziach?
Punkty 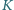 i
i 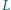 są środkami odpowiednio boków
są środkami odpowiednio boków 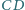 i
i 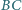 równoległoboku
równoległoboku 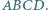 Udowodnij, że odcinki
Udowodnij, że odcinki 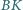 i
i 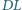 przecinają się na przekątnej
przecinają się na przekątnej 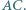
Sześciokąt 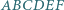 jest wpisany w okrąg i
jest wpisany w okrąg i 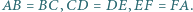 Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
Wykaż, że główne przekątne tego sześciokąta przecinają się w jednym punkcie.
Dany jest czworokąt wypukły 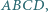 w którym
w którym 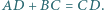 Dwusieczne kątów
Dwusieczne kątów 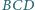 i
i 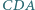 przecinają się w punkcie
przecinają się w punkcie 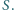 Udowodnij, że
Udowodnij, że 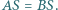
Wszystkie kąty wewnętrzne pięciokąta 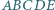 są równe. Symetralne odcinków
są równe. Symetralne odcinków 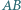 i
i  przecinają się w punkcie
przecinają się w punkcie 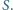 Wykaż, że proste
Wykaż, że proste 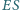 i
i 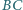 są prostopadłe.
są prostopadłe.
Na bokach 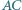 i
i 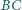 trójkąta
trójkąta 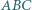 zbudowano, na zewnątrz, kwadraty
zbudowano, na zewnątrz, kwadraty 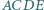 i
i 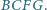 Udowodnij, że proste
Udowodnij, że proste 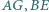 oraz wysokość
oraz wysokość 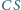 trójkąta
trójkąta 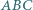 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Dwa rozwiązania zadania 6 przedstawiono w deltoidzie 11/2009.
Wykaż, że w dwunastokącie foremnym 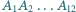 przekątne
przekątne 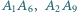 i
i 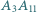 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Miara każdego kąta sześciokąta 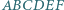 jest równa
jest równa 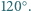 Udowodnij, że symetralne odcinków
Udowodnij, że symetralne odcinków 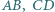 i
i 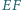 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Punkt 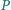 leży wewnątrz trójkąta
leży wewnątrz trójkąta 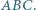 Punkty
Punkty 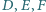 to punkty symetryczne do punktu
to punkty symetryczne do punktu 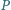 odpowiednio względem prostych
odpowiednio względem prostych 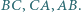 Wykaż, że jeśli trójkąt
Wykaż, że jeśli trójkąt 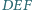 jest równoboczny, to proste
jest równoboczny, to proste 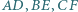 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Wykaż, że proste opisane w zadaniu 2 są też wysokościami trójkąta